Abstract
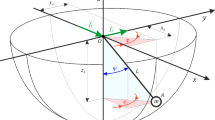
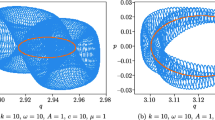
In this paper we study the global dynamics of the inverted spherical pendulum with a vertically rapidly vibrating suspension point in the presence of an external horizontal periodic force field. We do not assume that this force field is weak or rapidly oscillating. Provided that the period of the vertical motion and the period of the horizontal force are commensurate, we prove that there always exists a nonfalling periodic solution, i. e., there exists an initial condition such that, along the corresponding solution, the rod of the pendulum always remains above the horizontal plane passing through the pivot point. We also show numerically that there exists an asymptotically stable nonfalling solution for a wide range of parameters of the system.





Similar content being viewed by others
References
Stephenson, A., On Induced Stability, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (6), 1908, vol. 15, no. 86, pp. 233–236.
Bogolubov, N. N., Perturbation Theory in Nonlinear Mechanics, Sb. Tr. Inst. Stroit. Mekh. Akad. Nauk Ukr. SSR, 1950, no. 14, pp. 9–34 (Russian).
Kapitza, P. L., Pendulum with a Vibrating Suspension, Usp. Fiz. Nauk,1951, vol. 44, no. 1, pp. 7–20 (Russian). See also: Collected Papers of P. L. Kapitza: Vol. 2, D. ter Haar (Ed.), Oxford: Pergamon, 1965, pp. 726–737.
Kapitza, P. L., Dynamical Stability of a Pendulum When Its Point of Suspension Vibrates, Zh. Èksp. Teor. Fiz.,, 1951, vol. 21, no. 5, pp. 588–597 (Russian). See also: Collected Papers of P. L. Kapitza: Vol. 2, D. ter Haar (Ed.), Oxford: Pergamon, 1965, pp. 714–725.
Artstein, Z., The Pendulum under Vibrations Revisited, Nonlinearity, 2021, vol. 34, no. 1, pp. 394–410.
Cruz Araujo, G. and Cabral, H. E., Parametric Stability of a Charged Pendulum with an Oscillating Suspension Point, Regul. Chaotic Dyn., 2021, vol. 26, no. 1, pp. 39–60.
Belyaev, A. K., Morozov, N. F., Tovstik, P. E., Tovstik, T. M., and Tovstik, T. P., Classical Kapitsa’s Problem of Stability of an Inverted Pendulum and Some Generalizations, Acta Mech., 2021, vol. 232, no. 5, pp. 1743–1759.
Cabral, H. E. and Carvalho, A. C., Parametric Stability of a Charged Pendulum with Oscillating Suspension Point, J. Differential Equations, 2021, vol. 284, pp. 23–38.
Butikov, E. I., On the Dynamic Stabilization of an Inverted Pendulum, Am. J. Phys., 2001, vol. 69, no. 7, pp. 755–768.
Samoïlenko, A. M., N. N. Bogolyubov and Nonlinear Mechanics, Russian Math. Surveys, 1994, vol. 49, no. 5, pp. 109–154; see also: Uspekhi Mat. Nauk, 1994, vol. 49, no. 5(299), pp. 103-146.
Landa, P. S., Nonlinear Oscillations and Waves in Dynamical Systems, Math. Appl., vol. 360, Dordrecht: Springer, 2013.
Burd, V., Method of Averaging for Differential Equations on an Infinite Interval: Theory and Applications, Boca Raton, Fla.: Chapman & Hall/CRC, 2007.
Bardin, B. S. and Markeyev, A. P., The Stability of the Equilibrium of a Pendulum for Vertical Oscillations of the Point of Suspension, J. Appl. Math. Mech., 1995, vol. 59, no. 6, pp. 879–886; see also: Prikl. Mat. Mekh., 1995, vol. 59, no. 6, pp. 922-929.
Bartuccelli, M. V., Gentile, G., and Georgiou, K. V., KAM Theory, Lindstedt Series and the Stability of the Upside-Down Pendulum, Discrete Contin. Dyn. Syst., 2003, vol. 9, no. 2, pp. 413–426.
Markeyev, A. P., The Dynamics of a Spherical Pendulum with a Vibrating Suspension, J. Appl. Math. Mech., 1999, vol. 63, no. 2, pp. 205–211; see also: Prikl. Mat. Mekh., 1999, vol. 63, no. 2, pp. 213-219.
Grundy, R., A Two-Scale Analysis for a Spherical Pendulum with a Vertically Vibrating Pivot, Quart. J. Mech. Appl. Math., 2021, vol. 74, no. 2, pp. 137–157.
Petrov, A. G., On the Equations of Motion of a Spherical Pendulum with a Fluctuating Support, Dokl. Phys., 2005, vol. 50, pp. 588–592.
Srzednicki, R., Periodic and Bounded Solutions in Blocks for Time-Periodic Nonautonomous Ordinary Differential Equations, Nonlinear Anal. Theory Methods Appl., 1994, vol. 22, no. 6, pp. 707–737.
Bulanchuk, P. O. and Petrov, A. G., Controlling Spherical-Pendulum Motion with the Help of Suspension-Point Vibration, Dokl. Phys., 2010, vol. 55, no. 2, pp. 85–88; see also: Dokl. Akad. Nauk, 2010, vol. 430, no. 5, pp. 627-630.
Bolotin, S. V. and Kozlov, V. V., Calculus of Variations in the Large, Existence of Trajectories in Domains with Boundary, and Whitney’s Inverted Pendulum Problem, Izv. Math., 2015, vol. 79, no. 5, pp. 894–901; see also: Izv. Ross. Akad. Nauk Ser. Mat., 2015, vol. 79, no. 5, pp. 39-46.
Polekhin, I. Yu., The Method of Averaging for the Kapitza – Whitney Pendulum, Regul. Chaotic Dyn., 2020, vol. 25, no. 4, pp. 401–410.
Srzednicki, R., Wójcik, K., and Zgliczyński, P., Fixed Point Results Based on the Ważewski Method, in Handbook of Topological Fixed Point Theory, R. F. Brown, M. Furi, L. Górniewicz, B. Jiang (Eds.), Dordrecht: Springer, 2005, pp. 905–943.
Polekhin, I., Forced Oscillations of a Massive Point on a Compact Surface with a Boundary, Nonlinear Anal. Theory Methods Appl., 2015, vol. 128, pp. 100–105.
Sanders, J. A., Verhulst, F., and Murdock, J., Averaging Methods in Nonlinear Dynamical Systems, 2nd ed., Appl. Math. Sci., vol. 59, New York: Springer, 2007.
Funding
This work has been supported by the Grant of the President of the Russian Federation (Project MK-1826.2020).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The author declares that he has no conflicts of interest.
Additional information
MSC2010
34C29, 70K65, 34C25
Rights and permissions
About this article
Cite this article
Polekhin, I.Y. The Spherical Kapitza – Whitney Pendulum. Regul. Chaot. Dyn. 27, 65–76 (2022). https://doi.org/10.1134/S1560354722010075
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1560354722010075