Skip to main content
SpringerLink
Log in

Dynamics on the Double Morse Potential: A Paradigm for Roaming Reactions with no Saddle Points

  • Published:
Regular and Chaotic Dynamics Aims and scope Submit manuscript

Abstract

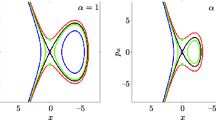
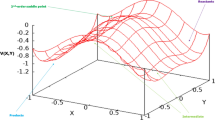
In this paper we analyze a two-degree-of-freedom Hamiltonian system constructed from two planar Morse potentials. The resulting potential energy surface has two potential wells surrounded by an unbounded flat region containing no critical points. In addition, the model has an index one saddle between the potential wells. We study the dynamical mechanisms underlying transport between the two potential wells, with emphasis on the role of the flat region surrounding the wells. The model allows us to probe many of the features of the “roaming mechanism” whose reaction dynamics are of current interest in the chemistry community.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Townsend, D., Lahankar, S. A., Lee, S.K., Chambreau, S.D., Suits, A.G., Zhang, X., Rheinecker, J., Harding, L. B., and Bowman, J.M., The Roaming Atom: Straying from the Reaction Path in Formaldehyde Decomposition, Science, 2004, vol. 306, no. 5699, pp. 1158–1161.

    Article  Google Scholar 

  2. Bowman, J.M. and Suits, A.G., Roaming Reactions: The Third Way, Phys. Today, 2011, vol. 64, no. 11, pp. 33–37.

    Article  Google Scholar 

  3. Bowman, J.M. and Shepler, B.C., Roaming Radicals, Annu. Rev. Phys. Chem., 2011, vol. 62, pp. 531–553.

    Article  Google Scholar 

  4. Suits, A.G., Roaming Atoms and Radicals: A New Mechanism in Molecular Dissociation, Acc. Chem. Res., 2008, vol. 41, no. 7, pp. 873–881.

    Article  Google Scholar 

  5. Mauguière, F. A., Collins, P., Kramer, Z. C., Carpenter, B.K., Ezra, G. S., Farantos, S.C., and Wiggins, S., Roaming: A Phase Space Perspective, Annu. Rev. Phys. Chem., 2017, vol. 68, pp. 499–524.

    Article  Google Scholar 

  6. Wiggins, S., Normally Hyperbolic Invariant Manifolds in Dynamical Systems, Appl. Math. Sci., vol. 105, New York: Springer, 2013.

    MATH  Google Scholar 

  7. Uzer, T., Jaffé, C., Palacián, J., Yanguas, P., and Wiggins, S., The Geometry of Reaction Dynamics, Nonlinearity, 2002, vol. 15, no. 4, pp. 957–992.

    Article  MathSciNet  MATH  Google Scholar 

  8. Wiggins, S., Wiesenfeld, L., Jaffé, C., Uzer, T., Impenetrable Barriers in Phase-Space, Phys. Rev. Lett., 2001, vol. 86, no. 24, pp. 5478–5481.

    Article  Google Scholar 

  9. Wiggins, S., The Role of Normally Hyperbolic Invariant Manifolds (NHIMs) in the Context of the Phase Space Setting for Chemical Reaction Dynamics, Regul. Chaotic Dyn., 2016, vol. 21, no. 6, pp. 621–638.

    Article  MathSciNet  MATH  Google Scholar 

  10. Mauguière, F. A., Collins, P., Kramer, Z. C., Carpenter, B.K., Ezra, G. S., Farantos, S.C., and Wiggins, S., Phase Space Structures Explain Hydrogen Atom Roaming in Formaldehyde Decomposition, J. Phys. Chem. Lett., 2015, vol. 6, no. 20, pp. 4123–4128.

    Article  Google Scholar 

  11. Morse, P. M., Diatomic Molecules According to the Wave Mechanics: 2. Vibrational Levels, Phys. Rev., 1929, vol. 34, no. 1, pp. 57–64.

    Article  MATH  Google Scholar 

  12. Borisov, A. V., Mamaev, I. S., and Bizyaev, I. A., The Spatial Problem of 2 Bodies on a Sphere: Reduction and Stochasticity, Regul. Chaotic Dyn., 2016, vol. 21, no. 5, pp. 556–580.

    Article  MathSciNet  MATH  Google Scholar 

  13. Moser, J., Stable and Random Motions in Dynamical Systems: With Special Emphasis on Celestial Mechanics, Ann. of Math. Stud., No. 77, Princeton, N.J.: Princeton Univ. Press, 2001.

    Book  MATH  Google Scholar 

  14. Verlet, L., Computer “Experiments” on Classical Fluids: 1. Thermodynamical Properties of Lennard–Jones Molecules, Phys. Rev., 1967, vol. 159, no. 1, pp. 98–103.

    Article  Google Scholar 

  15. Press, W. H., Teukolsky, S.A., Vetterling, W. T., and Flannery, B.P., Numerical Recipes: The Art of Scientific Computing, 3rd ed., New York: Cambridge Univ. Press, 2007.

    MATH  Google Scholar 

  16. Seoane, J.M. and Sanjuán, M.A. F., New Developments in Classical Chaotic Scattering, Rep. Prog. Phys., 2013, vol. 76, no. 1, 016001, 53 pp.

    Google Scholar 

  17. Carpenter, B. K., Nonstatistical Dynamics in Thermal Reactions of Polyatomic Molecules, Annu. Rev. Phys. Chem., 2005, vol. 56, pp. 57–89.

    Article  Google Scholar 

  18. Pechukas, P. and Pollak, E., Classical Transition State Theory Is Exact If the Transition State Is Unique, J. Chem. Phys., 1979, vol. 71, no. 5, pp. 2062–2068.

    Article  MathSciNet  Google Scholar 

  19. Pechukas, P. and Pollak, E., Trapped Trajectories at the Boundary of Reactivity Bands in Molecular Collisions, J. Chem. Phys., 1977, vol. 67, no. 12, pp. 5976–5977.

    Article  Google Scholar 

  20. Pollak, E., Child, M. S., and Pechukas, P., Classical Transition State Theory: A Lower Bound to the Reaction Probability, J. Chem. Phys., 1980, vol. 72, no. 3, pp. 1669–1678.

    Article  MathSciNet  Google Scholar 

  21. Pollak, E. and Pechukas, P., Transition States, Trapped Trajectories, and Classical Bound States Embedded in the Continuum, J. Chem. Phys., 1978, vol. 69, no. 3, pp. 1218–1226.

    Article  Google Scholar 

  22. Mauguière, F. A., Collins, P., Kramer, Z. C., Carpenter, B.K., Ezra, G. S., Farantos, S.C., and Wiggins, S., Phase Space Barriers and Dividing Surfaces in the Absence of Critical Points of the Potential Energy: Application to Roaming in Ozone, J. Chem. Phys., 2016, vol. 144, no. 5, 054107, 12 pp.

    Google Scholar 

  23. Carpenter, B. K., Ezra, G. S., Farantos, S.C., Kramer, Z.C., and Wiggins, S., Empirical Classification of Trajectory Data: An Opportunity for the Use of Machine Learning in Molecular Dynamics, J. Phys. Chem. B, 12 Oct 2017, DOI: 10.1021/acs.jpcb.7b08707.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Chemistry, Cardiff University, Cardiff, CF10 3AT, UK

    Barry K. Carpenter

  2. Department of Chemistry and Chemical Biology, Cornell University, Ithaca, NY, 14853-1301, USA

    Gregory S. Ezra

  3. Institute of Electronic Structure and Laser, Foundation for Research and Technology–Hellas, and Department of Chemistry, University of Crete, Iraklion, 711 10, Greece

    Stavros C. Farantos

  4. Department of Chemistry and Biochemistry, La Salle University, 1900 West Olney Avenue, Philadelphia, PA, 19141, USA

    Zeb C. Kramer

  5. School of Mathematics, University of Bristol, Bristol, BS8 1TW, UK

    Stephen Wiggins

Authors
  1. Barry K. Carpenter
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gregory S. Ezra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Stavros C. Farantos
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zeb C. Kramer
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Stephen Wiggins
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Barry K. Carpenter.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Carpenter, B.K., Ezra, G.S., Farantos, S.C. et al. Dynamics on the Double Morse Potential: A Paradigm for Roaming Reactions with no Saddle Points. Regul. Chaot. Dyn. 23, 60–79 (2018). https://doi.org/10.1134/S1560354718010069

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1560354718010069

MSC2010 numbers

Keywords

Search

Navigation