Abstract
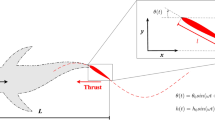
Most aquatic vertebrates swim by lateral flapping of their bodies and caudal fins. While much effort has been devoted to understanding the flapping kinematics and its influence on the swimming efficiency, little is known about the stability (or lack of) of periodic swimming. It is believed that stability limits maneuverability and body designs/flapping motions that are adapted for stable swimming are not suitable for high maneuverability and vice versa. In this paper, we consider a simplified model of a planar elliptic body undergoing prescribed periodic heaving and pitching in potential flow. We show that periodic locomotion can be achieved due to the resulting hydrodynamic forces, and its value depends on several parameters including the aspect ratio of the body, the amplitudes and phases of the prescribed flapping.We obtain closedform solutions for the locomotion and efficiency for small flapping amplitudes, and numerical results for finite flapping amplitudes. This efficiency analysis results in optimal parameter values that are in agreement with values reported for some carangiform fish. We then study the stability of the (finite amplitude flapping) periodic locomotion using Floquet theory. We find that stability depends nonlinearly on all parameters. Interesting trends of switching between stable and unstable motions emerge and evolve as we continuously vary the parameter values. This suggests that, for live organisms that control their flapping motion, maneuverability and stability need not be thought of as disjoint properties, rather the organism may manipulate its motion in favor of one or the other depending on the task at hand.
Similar content being viewed by others
References
Lighthill, M. J., Aquatic Animal Propulsion of High Hydromechanical Efficiency, J. Fluid Mech., 1970, vol. 44, no. 2, pp. 265–301.
Wu, T.Y., Fish Swimming and Bird/Insect Flight, Annu. Rev. Fluid Mech., 2011, vol. 43, no. 1, pp. 25–58.
Eloy, C., On the Best Design for Undulatory Swimming, J. Fluid Mech., 2013, vol. 717, pp. 48–89.
Weihs, D., Stability Versus Maneuverability in Aquatic Locomotion, Integ. and Comp. Biol., 2002, vol. 42, no. 1, pp. 127–134.
Weihs, D., Stability of Aquatic Animal Locomotion, Cont. Math., 1993, vol. 141, pp. 443–461.
Jordan, D.W. and Smith, P., Nonlinear Ordinary Differential Equations: An Introduction to Dynamical Systems, 4th ed., New York: Oxford Univ. Press, 2007.
Kanso, E., Marsden, J.E., Rowley, C.W., and Melli-Huber, J. B., Locomotion of Articulated Bodies in a Perfect Fluid, J. Nonlinear Sci., 2005, vol. 15, pp. 255–289.
Jing, F., Part 1. Viscous Evolution of Point Vortex Equilibria, Part 2. Effects of Body Elasticity on Stability of Fish Motion, PhD Thesis, University of Southern California, Los Angeles, 2011.
Jing, F. and Kanso, E., Effects of Body Elasticity on Stability of Underwater Locomotion, J. Fluid Mech., 2012, vol. 690, pp. 461–473.
Spagnolie, S.E., Moret, L., Shelley, M. J., and Zhang, J., Surprising Behaviors in Flapping Locomotion with Passive Pitching, Phys. Fluids, 2010, vol. 22, 041903, 20 pp.
Newman, J.N., Marine Hydrodynamics, Cambridge, MA: MIT Press, 1977.
Kern, S. and Koumoutsakos, P., Simulations of Optimized Anguilliform Swimming, J. Exp. Biol., 2006, vol. 209, pp. 4841–4857.
Jayne, B.C. and Lauder, G.V., Red Muscle Motor Patterns during Steady Swimming in Largemouth Bass: Effects of Speed and Correlations with Axial Kinematics, J. Exp. Biol., 1995, vol. 198, pp. 1575–1587.
Donley, J.M. and Dickson, K. A., Swimming Kinematics of Juvenile Kawakawa Tuna (Euthynnus affinis) and Chub Mackerel (Scomber japonicus), J. Exp. Biol., 2000, vol. 203, pp. 3103–3116.
Videler, J. J. and Hess, F., Fast Continuous Swimming of Two Pelagic Predators, Saithe (Pollachius virens) and Mackerel (Scomber scombrus): A Kinematic Analysis, J. Exp. Biol., 1984, vol. 109, pp. 209–228.
Triantafyllou, M. S., Hover, F. S., Techet, A.H., and Yue, D.K.P., Review of Hydrodynamic Scaling Laws in Aquatic Locomotion and Fishlike Swimming, Appl. Mech. Rev., 2005, vol. 58, no. 4, pp. 226–237.
Jing, F. and Alben, S., Optimization of Two- and Three-Link Snakelike Locomotion, Phys. Rev. E, 2013, vol. 87, 022711, 15 pp.
Lamb, H., Hydrodynamics, 6th ed., Cambridge: Cambridge Univ. Press, 1932.
Sedov, L. I., Two-Dimensional Problems in Hydrodynamics and Aerodynamics, C. K. Chu, H. Cohen, B. Seckler, J. Gillis (Eds.), New York: Intersci. Publ., 1965.
Milne-Thomson, L.M., Theoretical Hydrodynamics, New York: Dover Publications, 1968.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jing, F., Kanso, E. Stability of underwater periodic locomotion. Regul. Chaot. Dyn. 18, 380–393 (2013). https://doi.org/10.1134/S1560354713040059
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1560354713040059