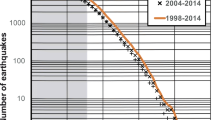
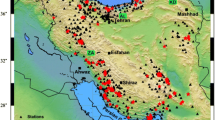
Abstract
A step-by-step scheme of space-time earthquake probability prediction is constructed as a realization of a general mathematical model. The scheme uses four predictors based on concepts of fracture. Prediction results for California and the Sumatra-Andaman earthquake region are presented. Dangers inherent in the use of purely empirical predictors are discussed. An upper estimate is obtained for the admissible number of predictor parameters.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. M. Ghertzik, “Equations of Dynamics of a Seismogenic Continuous Medium,” in Modern Methods of Seismological Data Interpretation, Vol. 24 of Computational Seismology (Nauka, Moscow, 1991), pp. 62–75 [in Russian].
V. M. Ghertzik, “Mathematical Principles of Predicting the Probabilities of Large Earthquakes,” Fiz. Zemli, No. 6, 21–31 (2006) [Izvestiya, Phys. Solid Earth 42, 467–476 (2006)].
J. N. Goodier, “Mathematical Theory of Equilibrium Cracks,” in Mathematical Fundamentals, Vol. 2 of Fracture, Ed. by H. Liebovitz (Mir, Moscow, 1975), pp. 13–83 [in Russian].
A. N. Kolmogorov, “On the Suitability of Statistically Obtained Prediction Formulas,” Zh. Geofiz. 3, 78–82 (1933).
A. N. Krichevets, The Problem of Conditions of a Possible Experiment in Mathematics, Psychology, and Artificial Intelligence, Doctoral (Philosophy) Dissertation, Lomonosov Moscow State Univ., Moscow, 2000.
H. Liebovitz, “Mathematical Theories of Brittle Fracture,” in Mathematical Fundamentals, Vol. 2 of Fracture, Ed. by H. Liebovitz (Mir, Moscow, 1975), pp. 83–203 [in Russian].
E. N. Lorenz, Prospects for Statistical Weather Forecasting (Statist. Forecasting Proj. Final Rept.) (Cambridge (Mass.), 1959).
G. A. Sobolev, Fundamentals of Earthquake Prediction (Nauka, Moscow, 1993) [in Russian].
G. A. Sobolev and A. D. Zavyalov, “Approach to Dynamic Seismic Hazard Map,” in XX General Assembly IUGG: Program and Abstracts (IASPEI, Vienna, 1991), p. 12.
A. M. Yaglom, “Statistical Prediction,” and A. N. Kolmogorov, “Theory of Probabilities and Mathematical Statistics,” in Collection of Papers, Ed. by N. N. Bogolyubov (Nauka, Moscow, 1986) [in Russian].
A. D. Zavyalov, “Concentration Parameter of Seismogenic Faults as a Precursor of Strong Earthquakes in the Kamchatka Region,” Vulkanol. Seismol., No. 3, 58–71 (1986).
S. N. Zhurkov, V. S. Kuksenko, and A. I. Slutsker, “Formation of Submicroscopic Cracks in Loaded Polymers,” Fiz. Tverd. Tela, No. 11, 296 (1969).
Author information
Authors and Affiliations
Additional information
Original Russian Text © V.M. Ghertzik, 2008, published in Fizika Zemli, 2008, No. 3, pp. 22–39.
Rights and permissions
About this article
Cite this article
Ghertzik, V.M. Physical concepts of fracture and prediction of probabilities of strong earthquakes. Izv., Phys. Solid Earth 44, 193–208 (2008). https://doi.org/10.1134/S1069351308030038
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1069351308030038