Abstract
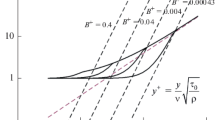
A closed system of equations for describing turbulent flows is obtained. Additional equations for the cross pulsation moments \(\rho \overline {\Delta {{u}_{i}}\Delta {{u}_{k}}} \) are derived using a balanced kinetic equation, which was previously used to obtain a quasi-gasdynamic system of equations. Numerical results for the problem of a two-dimensional mixing layer between two flows are presented.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
L. G. Loitsyanskii, Mechanics of Liquids and Gases, 2nd revised ed. (Pergamon, Oxford, 2014).
P. R. Spalart and S. R. Allmaras, “A one-equation turbulence model for aerodynamic flows,” Recherche Aerospatiale, No. 1, 5–21 (1994).
M. Shur, M. Strelets, L. Zaikov, A. Gulyaev, V. Kozlov, and A. Secundov, “Comparative numerical testing of one and two equation turbulence models for flows with separation and reattachment,” AIAA Paper, No. 95-0863 (1995).
I. A. Ivakhnenko, S. V. Polyakov, and B. N. Chetverushkin, “Quasi-hydrodynamic model and small scale turbulence,” Math. Models Comput. Simul. 1 (1), 44–50 (2006).
D. E. Wilcox, “Formulation of the K-omega turbulence model revisited,” AIAA J. 46 (11), 2823–2838 (2008).
I. V. Abalakin, A. N. Antonov, I. A. Graur, and B. N. Chetverushkin, “Application of an algebraic turbulent model to unsteady flow simulation around a cavity,” Mat. Model. 12 (1), 45–56 (2000).
F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications,” AIAA J. 32 (8), 1598–1605 (1994).
U. Goldberg, O. Peroomian, P. Batten, and S. Chakravarthy, “The k-ε-Rt turbulence closure,” Eng. Appl. Comput. Fluid Mech. 3 (2), 175–183 (2009).
K. S. Abdol-Hamid, J.-R. Carlson, and C. L. Rumsey, “Verification and validation of the K-KL turbulence model in FUN 3D and CFL 3D codes,” AIAA Paper, No. 2016–3941 (2016).
U. Frisch, Turbulence: The Legacy of A.N. Kolmogorov (Cambridge Univ. Press, Cambridge, 1995).
B. N. Chetverushkin, Kinetic Schemes and Quasi-Gas Dynamic System of Equations (MAKS, Moscow, 2004; CIMNE, Barcelona, 2008).
J. O. Hirschfelder, C. F. Curtiss, and R. B. Bird, The Molecular Theory of Gases and Liquids (Wiley, New York, 1954).
A. A. Zlotnik and B. N. Chetverushkin, “On a hyperbolic perturbation of a parabolic initial boundary value problem,” Appl. Math. Lett. 83, 116–122 (2018).
A. A. Zlotnik and B. N. Chetverushkin, “Properties and errors of second-order parabolic and hyperbolic perturbations of a first-order symmetric hyperbolic system,” Sb. Math. 214 (4), 444–478 (2023).
B. N. Chetverushkin, A. V. Saveliev, and V. A. Saveliev, “Kinetic algorithms for modeling conductive fluids flow on high-performance computing systems,” Dokl. Math. 100 (3), 577–581 (2019).
B. N. Chetverushkin, A. V. Saveliev, and V. A. Saveliev, “Kinetic consistent MHD algorithm for incompressible conductive fluids,” Comput. Fluids 255, 105724 (2023).
S. Chapman and T. G. Cowling, Mathematical Theory of Nonuniform Gases (Cambridge Univ. Press, Cambridge, 1952).
C. Cercignani, Mathematical Methods in Kinetic Theory (Plenum, New York, 1969).
Funding
This work was supported by ongoing institutional funding. No additional grants to carry out or direct this particular research were obtained.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
The authors of this work declare that they have no conflicts of interest.
Additional information
Translated by I. Ruzanova
Publisher’s Note.
Pleiades Publishing remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chetverushkin, B.N., Lutsky, A.E. & Shilnikov, E.V. Description of Turbulent Flows Using a Kinetic Model. Dokl. Math. (2024). https://doi.org/10.1134/S1064562424701953
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1134/S1064562424701953