Abstract
Axiom A diffeomorphisms of closed 2-manifold of genus \(p \geqslant 2\) whose nonwandering set contains a perfect spaciously situated one-dimensional attractor are considered. It is shown that such diffeomorphisms are topologically semiconjugate to a pseudo-Anosov homeomorphism with the same induced automorphism of fundamental group. The main result of this paper is as follows. Two diffeomorphisms from the given class are topologically conjugate on perfect spaciously situated attractors if and only if the corresponding homotopic pseudo-Anosov homeomorphisms are topologically conjugate by means of a homeomorphism that maps a certain subset of one pseudo-Anosov homeomorphism onto a subset of the other.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
A basic set \(\Lambda \) of an\(A\)-diffeomorphism f is called an attractor if there exists a closed neighborhood U of \(\Lambda \) such that \(f(U) \subset {\text{int}}U\), \(\bigcap\limits_{j \geqslant 0} \,{{f}^{j}}(U) = \Lambda \). An attractor of the diffeomorphism \({{f}^{{ - 1}}}\) is called a repeller of the diffeomorphism \(f\).
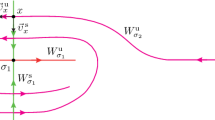
\({{[x,y]}^{s}},{{[x,y]}^{s}},{{(x,y)}^{u}},{{(x,y)}^{u}}\) denote closed and open intervals bounded by the points \(x,y\) that are contained in the one-dimensional stable \(W_{x}^{s}\) and unstable \(W_{x}^{u}\) manifolds, respectively.
For a domain \(\Delta \), its boundary accessible from within is defined as a subset \(C \subset \Lambda \) with the following property: for any point \(y \in C,\) there exists a path \({{\psi }_{y}}:I \to \Delta \cup C\) such that \({{\psi }_{y}}(1) = y\) and \({{\psi }_{y}}(t) \in \Delta \) for any \(t \in [0,1)\).
REFERENCES
V. Z. Grines, J. Math. Sci. 95 (5), 2523–2545 (1999).
V. Z. Grines, J. Dyn. Control Syst. 6 (1), 97–126 (2000).
A. Fathi, F. Laudenbach, and V. Poenaru, Thurston’s Work on Surfaces (Princeton Univ. Press, Princeton, 2012), Vol. 48.
A. J. Casson and S. A. Bleiler, Automorphisms of Surfaces after Nielsen and Thurston (Cambridge Univ. Press, Cambridge, 1988).
A. Yu. Zhirov and R. V. Plykin, Math. Notes 58 (1), 779–781 (1995).
V. Z. Grines, Tr. Mosk. Mat. Ob–va 32, 35–59 (1975).
V. Z. Grines, Tr. Mosk. Mat. Ob–va 34, 243–252 (1977).
R. V. Plykin, Math. USSR-Sb. 13 (2), 297–307 (1971).
R. V. Plykin, Math. USSR-Sb. 23 (2), 233–253 (1974).
S. Smale, Bull. Am. Math. Soc. 73 (6), 747–817 (1967).
A. Yu. Zhirov, Topological Conjugacy of Pseudo-Anosov Homeomorphisms (MTsNMO, Moscow, 2014) [in Russian].
ACKNOWLEDGMENTS
This work was supported by the Russian Science Foundation, project no. 17-11-01041.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by I. Ruzanova
Rights and permissions
About this article
Cite this article
Grines, V.Z., Kurenkov, E.D. Classification of One-Dimensional Attractors of Diffeomorphisms of Surfaces by Means of Pseudo-Anosov Homeomorphisms. Dokl. Math. 99, 137–139 (2019). https://doi.org/10.1134/S1064562419020066
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1064562419020066