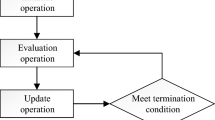
Abstract
This paper describes the algorithm for averaging the orbital parameters of the International Space Station (ISS), which was implemented for the International Cooperation for Animal Research Using Space (ICARUS) experiment aboard the ISS. Based on the ballistic and navigational information received from the control system, the algorithm aboard the station calculates the orbital motion parameters in the Two Line Elements format. The acquired data are averaged using the least-square method. To ensure the algorithm’s execution on the platform of the ISS onboard computer in a realtime system, the process of calculations is distributed over computational cycles. The efficiency of the proposed algorithm is demonstrated using the results of mathematical simulation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. Yu. Belyaev, M. Vikel’ski, M. Lampen, et al., “Technology for studying movements of animals and birds on earth using ICARUS equipment on the Russian segment of the ISS,” Kosm. Tekh. Tekhnol., No. 3, 38–51 (2015).
A. V. Sumarokov, “High resolution camera point during Earth’ surface video recording from ISS,” in Proceedings of the 17th Conference of Young Scientists on Navigation and Motion Control, Ed. by V. G. Peshekhonov (Elektropribor, St. Petersburg, 2015), pp. 561–568.
A. V. Sumarokov, “On pointing of high resolution camera mountedon the International Space Station using biaxial rotating platform,” Vestn. Mosk. Tekh. Univ. im. N. E. Baumana, Ser. Priborostroen., No. 4, 85–97 (2016).
M. Yu. Belyaev, L. V. Desinov, D. Yu. Karavaev, et al., “Features of imaging the Earth surface and using the results of the imaging made by the ISS Russian segment crews,” Kosm. Tekh. Tekhnol., No. 1, 17–30 (2015).
F. R. Hoots and R. L. Roehrich, “Models for propagation of NORAD element sets,” Spacetrack Report No. 3 (Aerospace Defense Center, Peterson Air Force Base, Peterson, 1980).
D. A. Vallado, Fundamentals of Astrodynamics and Applications (Microcosm Press, Kluwer Academic, El Segundo, Dordrecht, 2001).
F. A. Voronin, P. A. Pakhmutov, and A. V. Sumarokov, “On information-control system modernization introduced in the Russian segment of International Space Station,” Vestn. Mosk. Tekh. Univ. im. N. E. Baumana, Ser. Priborostroen., No. 1, 109–122 (2017).
A. V. Sumarokov, “On parameters averaging of ISS orbital motion in space experiment GTS2,” in Proceedings of the 16th Conference of Young Scientists on Navigation and Motion Control, Ed. by V. G. Peshekhonov (Elektropribor, St. Petersburg, 2014), pp. 334–341.
D. A. Vallado and P. Crawford, “SGP4 orbit determination,” in Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibition on Guidance, Navigation, and Control and Co-located Conference, Honolulu, 2008.
P. E. El’yasberg, Introduction to the Theory of Flight of Artificial Earth Satellites (Nauka, Moscow, 1965; Israel Program Sci. Transl., Jerusalem, 1967).
Yu. V. Linnik, The Method of Least Squares and the Principles of the Mathematical-Statistical Theory of Processing of Observations (Fizmatgiz, Moscow, 1958) [in Russian].
G. Korn and T. Korn, Mathematical Handbook for Scientists and Engineers (Nauka, Moscow, 1968; McGraw-Hill, New York, 1961).
D. V. Beklemishev, Additional Chapters of Linear Algebra (Nauka, Moscow, 1983) [in Russian].
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © A.V. Sumarokov, 2018, published in Izvestiya Akademii Nauk, Teoriya i Sistemy Upravleniya, 2018, No. 2, pp. 102–111.
Rights and permissions
About this article
Cite this article
Sumarokov, A.V. The Onboard Algorithm for Averaging the Orbital Motion Parameters of the International Space Station in the ICARUS Experiment. J. Comput. Syst. Sci. Int. 57, 273–282 (2018). https://doi.org/10.1134/S1064230718010124
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1064230718010124