Precision program guidance of an nonrigid orbital telescope

Abstract

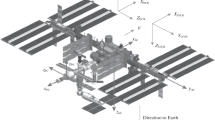
New capabilities of direct numerical technology for calculation of open-loop controls for nonlinear objects are considered. The modification of direct algorithm closed with respect to the output of the complete model predicting the state of a nonrigid controlled object is presented. According to this algorithm the control law is iteratively calculated using a reduced system with the order considerably lower than the complete model. The new algorithm provides calculation of high accuracy and low-sensitive to inaccuracy of initial data (Tikhonov stable, or robust) open-loop control for dynamic models with high dimensionality. The operation of the modified algorithm is demonstrated for the calculation of the open-loop control for the regime of reorientation of an orbital telescope whose dynamic model takes into account the flexibility of its structural elements as an example. The objective of the numerical experiment is the analysis of the influence on dynamics of the programmed controlled process of essential perturbations of the model: changes in its structure (due to the account offlexibility of solar panels), parameters (spread of moments of partial tones of solar panels, coefficients of inertial coupling of partial tones of solar panels and the telescope frame, and eigenfrequencies of solar panels) was considered. Results of calculations testify that the theoretically established property of stability of direct algorithm to errors of initial data (well conditioned algorithm) provides robustness and, at the same time, a high accuracy open-loop control according to laws calculated using the direct method.