Skip to main content
SpringerLink
Log in

New Design of Wavelets Based on the Convolution of Compactly Supported Functions with a Rectangular Pulse

  • THEORY AND METHODS OF SIGNAL PROCESSING
  • Published:
Journal of Communications Technology and Electronics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

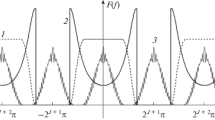
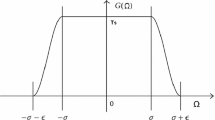
Abstract

A new design of wavelets based on the convolution of a compactly supported function with a rectangular pulse is proposed and theoretically substantiated and an efficient scheme for calculating wavelet values is presented. The uncertainty constants are calculated. It is established that the obtained wavelets have properties similar to those of the Meyer and Kravchenko wavelets but surpass the latter in the time‒frequency localization quality.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.

Similar content being viewed by others

REFERENCES

  1. Y. Meyer, Wavelets and Operators (Cambridge Univ. Press, Cambridge, 1993).

    Book  Google Scholar 

  2. S. G. Mallat, A Wavelet Tour of Signal Processing (Academic, San Diego, 1998; Mir, Moscow, 2005).

  3. I. Ya. Novikov, V. Yu. Protasov, and M. A. Skopina, Theory of Splashes (Fizmatlit, Moscow, 2006) [in Russian].

    Google Scholar 

  4. V. F. Kravchenko and D. V. Churikov, Usp. Sovr. Radioelektron., No. 6, 67 (2008).

  5. V. F. Kravchenko and A. V. Yurin, Usp. Sovr. Radioelektron., No. 5, 3 (2008).

  6. V. F. Kravchenko and O. V. Kravchenko, Constructive Methods of Algebra of Logic, Atomic Functions, Wavelets, Fractals in Problems of Physics and Engineering, Ed. by V. F. Kravchenko (Tekhnosfera, Moscow, 2018) [in Russian].

    Google Scholar 

  7. V. F. Kravchenko, H. M. Perez-Meana, and V. I. Pono-maryov, Adaptive Digital Processing of Multidimensional Signals with Applications (Fizmatlit, Moscow, 2009) [in Russian].

    Google Scholar 

  8. V. F. Kravchenko, O. V. Kravchenko, Y. Y. Konovalov, and K. A. Budunova, in Proc. Conf. IEEE Ukrainian Microwave Week (UkrMW), Kharkiv, Ukraine, 21–25 Sept. 2020 (IEEE, New York, 2020).

  9. Y. Y. Konovalov, in PhotonIcs & Electromagnetics Research Symp.—Spring (PIERS-Spring), Italy, June, Rome, 2019, p. 114. https://doi.org/10.1109/PIERS-Spring46901.2019.9017707

  10. Ya. Yu. Konovalov, Fiz. Osn. Priborostr. 9 (2), 48 (2020). https://doi.org/10.25210/jfop-2002-048059

    Article  Google Scholar 

  11. V. F. Kravchenko and D. V. Churikov, Digital Signal Processing by Signals Atomic Functions and Wavelets, Ed. by V. F. Kravchenko (Tekhnosfera, Moscow, 2018) [in Russian].

    Google Scholar 

  12. V. F. Kravchenko and V. I. Pustovoit, Dokl. Math. 80, 775 (2009).

    Article  MathSciNet  Google Scholar 

  13. V. F. Kravchenko, O. V. Kravchenko, V. I. Pustovoit, D. V. Churikov, and A. V. Yurin, J. Commun. Technol. Electron. 60, 103 (2015).

    Article  Google Scholar 

  14. V. F. Kravchenko, V. I. Pustovoit, and D. V. Churikov, Dokl. Phys. 56, 471 (2011).

    Article  Google Scholar 

  15. V. F. Kravchenko and A. V. Yurin, Elektromagn. Volny & Elektron. Sist. 13 (8), 12 (2008).

    Google Scholar 

  16. V. F. Kravchenko, O. V. Kravchenko, Ya. Yu. Kono-valov, and D. V. Churikov, in Proc. Int. Conf. Days on Diffraction 2015, Saint Petersburg, Russia, May 2015, p. 180. https://doi.org/10.1109/DD.2015.7354856

  17. V. F. Kravchenko, Ya. Yu. Konovalov, and V. I. Pustovoit, J. Commun. Technol. Electron. 60, 986 (2015).

    Article  Google Scholar 

  18. V. F. Kravchenko and Ya. Yu. Konovalov, in Proc. 14th Int. Sci.-Tech. Conf. “Optical-Acoustic and Radar Methods of Measurements and Information Processing,” Astrakhan’, Oct. 5–7, 2021, Vol. 14, p. 97. https://doi.org/10.25210/armimp-2021-27

  19. V. F. Kravchenko and Ya. Yu. Konovalov, Photonics & Electromagnetics Research Symp. (PIERS), 204 (2021). https://doi.org/10.1109/PIERS53385.2021.9695100

Download references

Author information

Authors and Affiliations

  1. Kotelnikov Institute of Radioengineering and Electronics, Russian Academy of Sciences, 125009, Moscow, Russia

    V. F. Kravchenko

  2. Scientific and Technological Center of Unique Instrumentation, Russian Academy of Sciences, 117342, Moscow, Russia

    V. F. Kravchenko

  3. Bauman Moscow State Technical University, 105005, Moscow, Russia

    V. F. Kravchenko & Ya. Yu. Konovalov

Authors
  1. V. F. Kravchenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ya. Yu. Konovalov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. F. Kravchenko or Ya. Yu. Konovalov.

Ethics declarations

The authors declare that they have no conflicts of interest.

Additional information

Translated by E. Bondareva

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kravchenko, V.F., Konovalov, Y.Y. New Design of Wavelets Based on the Convolution of Compactly Supported Functions with a Rectangular Pulse. J. Commun. Technol. Electron. 67, 952–964 (2022). https://doi.org/10.1134/S1064226922080095

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1064226922080095

Search

Navigation