Skip to main content
SpringerLink
Log in

Stationary characteristics of M 2|G|1|r system with hysteretic policy for arrival rate control

  • Mathematical Models and Computational Methods
  • Published:
Journal of Communications Technology and Electronics Aims and scope Submit manuscript

Abstract

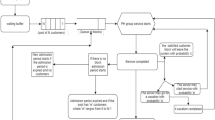
A finite queuing system with one server, Poisson input flow, arbitrary service time distribution, and hysteretic policy for arrival rate control is considered. An analytical method is proposed for determination of the stationary distribution of the number of customers in the system. Several numerical examples are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. O. Abaev, Yu. V. Gaidamaka, and K. E. Samuilov, “Hysteresis management of signal workload in net of SIP-servers,” Vestn. Ross. Univ. Druzhby Narodov, Mat. Inf. Fiz., No. 4, 54–71 (2011).

    Google Scholar 

  2. Dshalalow J.H. “Queueing systems with state dependent parameters,” in Frontiers in Queueing: Models and Applications in Science and Engineering (CRC, Boca Raton, 1997), pp. 61–116.

    Google Scholar 

  3. Kitaev M.Yu. and Rykov V.V. Controlled Queueing Systems (CRC, New York, 1995).

    MATH  Google Scholar 

  4. R. Bekker and O. J. Boxma “An M/G/1 queue with adaptable service speed,” Stoch. Models 23, 373–396 (2007).

    Article  MATH  MathSciNet  Google Scholar 

  5. A. Chydzinski, “The oscillating queue with finite buffer,” Perform. Eval. 57, 341–355 (2004).

    Article  Google Scholar 

  6. A. Chydzinski A. “The M/G-G/1 Oscillating Queueing System,” Queueing Syst. 42, 255–268 (2002).

    Article  MATH  MathSciNet  Google Scholar 

  7. A. M. Gortsev, “Queueing system with an arbitrary number of standby channels and hysteretic control of switching-on and switching-off of standby circuits,” Avtom. Telemekh., No. 10, 30–37 (1977).

    Google Scholar 

  8. A. Dudin, “Optimal control for an M x|G|1 queue with two operation modes,” Probab. Eng. Inf. Sci. 11, 255–265 (1997).

    Article  MATH  MathSciNet  Google Scholar 

  9. K. Yu. Zhernovyi and Yu. V. Zhernovyi, “An Mθ/G/1/m system with two-threshold hysteresis strategy of service intensity switching,” Inf. Protsessy 12, 127–140 (2012).

    Google Scholar 

  10. S. Nishimura and Y. Jiang. “An M|G|1 vacation model with two service modes,” Probab. Eng. Inf. Sci., 9, 355–374 (1995).

    Article  MathSciNet  Google Scholar 

  11. K. Yu. Zhernovyi and Yu. V. Zhernovyi, “An Mθ/G/1 system with hysteretic switching of the service intensity,” Inf. Protsessy 12, 176–190 (2012).

    Google Scholar 

  12. B. D. Choi and D. I. Choi, “The queueing system with queue length dependent service times and its application to cell discarding scheme in ATM networks,” IEE Proc. Comm. 143, 5–11 (1996).

    Article  Google Scholar 

  13. A. Segkhaier and I. I. Tsitovich, “On an interval model for a hysteretic process of birth and death,” Inf. Protsessy 12, 117–126 (2012).

    Google Scholar 

  14. L. Gyemin and J. Jongwoo, “Analysis of an MMPP|G|1|K finite queue with two-level threshold overload control,” Commun. Korean Math. Soc. 14, 805–814 (1999).

    MATH  MathSciNet  Google Scholar 

  15. D. I. Choi, “Analysis of a queueing system with overload control by arrival rates,” J. Appl. Math. Comput. 18, 455–464 (2005).

    Google Scholar 

  16. B. Van Houdt, “Analysis of the adaptive MMAP(K)|PH(K)|1 queue: A multi-type queue with adaptive arrivals and general impatience,” Eur. J. Operat. Res., 220, 695–704 (2012).

    Article  MATH  Google Scholar 

  17. I. Usar and I. Makushenko, “Hysteretic strategy for a system with repeated calls,” in Modern Probabilistic Methods for Analysis and Optimization of Information and Telecommunication Networks (Proc. Int. Conf., Minsk, Jan. 31–Feb. 3, 2011) (RIVSh, Minsk, 2011), pp. 253–257.

    Google Scholar 

  18. R. Bekker, “Queues with Levy input and hysteretic control,” Queueing Syst. 63, 281–299 (2009).

    Article  MATH  MathSciNet  Google Scholar 

  19. T. A. Milovanova and A. V. Pechinkin, “Stationary characteristics of a service system with inversion service, probabilistic priority, and hysteretic politics,” Inf. Primenen. 7(1), 26–38 (2013).

    Google Scholar 

  20. Yu. Gaidamaka, K. Samouylov, and E. Sopin, “Analysis of M/G/1 Queue with Hysteresis Load Control.,” in Proc. 30th Int. Seminar on Stability Problems for Stochastic Models and 6th Int. Workshop Applied Problems in Theory of Probabilities and Mathematical Statistics Related to Modeling of Information Systems (Institute of Informatics Problems, RAS, Moscow, 2012), pp. 87–89.

    Google Scholar 

  21. E. Sopin, “Analysis of M|G|1|r Queue with Batch Arrival and Hysteresis Overload Control,” Vestn. Ross. Univ. Druzhby Narodov, No. 4, 38–44 (2013).

    Google Scholar 

  22. P. Abaev, Yu. Gaidamaka, and K. Samouylov, “Queuing Model for Loss-Based Overload Control in a SIP Server Using a Hysteresis Technique,” in Lecture Notes in Computer Science (Heidelberg, Springer-Verlag, 2012), Vol. 7469, pp. 371–378.

    Google Scholar 

  23. P. Abaev, Yu. Gaidamaka, and K. Samouylov, “Modeling of Hysteresis Signaling Load Control in Next Generation Networks,” in Lecture Notes in Computer Science (Heidelberg, Springer-Verlag, 2012), Vol. 7469, pp. 440–452.

    Google Scholar 

  24. P. Bocharov, D’Apice C., A. Pechinkin, S. Salerno, Queueing Theory (VSP Publishing, Utrecht, 2003).

    Book  Google Scholar 

  25. P. Abaev, Yu. Gaidamaka, A. Pechinkin, R. Razum- chik, S. Shorgin, “Simulation of overload control in SIP server networks,” in Proc. 26th Eur. Conf. on Modelling and Simulation, Koblenz, Germany, May 29th–June 1st, 2012 (School of Science and Technology Nottingham Trent Univ., Nottingham, 2012), pp. 533–539.

    Google Scholar 

  26. P. Abaev, A. Pechinkin, and R. Razumchik, “Analysis of queueing system with constant service time for sip server hop-by-hop overload control,” in Lecture Notes in Communications in Computer and Information Science (Heidelberg, Springer-Verlag, 2012), Vol. 272, 1–10 (2013).

    Google Scholar 

  27. P. Abaev, A. Pechinkin, and R. Razumchik, “On analytical model for optimal sip server hop-by-hop overload control,” in Proc. of the 4th Int. Congr. on Ultra Modern Telecommun. and Control Syst., St. Petersburg, Russia, Oct. 3–5, 2012 (IEEE, New York, 2012), pp. 303–308.

    Google Scholar 

  28. A. Pechinkin and R. Razumchik, “Approach for analysis of finite M 2|M 2|1|R with hysteresis policy for sip server hop-by-hop overload control,” in Proc. 27th Eur. Conf. on Modelling and Simulation, Alesund, Norway, May 27–30, 2013 (Aalesund Univ. College, Aalesund, 2013), pp. 573–579.

    Google Scholar 

  29. P. Abaev and R. Razumchik, “Queuing Model for SIP Server Hysteresis Overload Control with Bursty Traffic,” in Proc. of the 13th Int. Conf. on Next Generation Wired/Wireless Networking, St. Petersburg, Russia, Aug., 2013.

Download references

Author information

Authors and Affiliations

  1. Institute of Informatics Problems, Russian Academy of Sciences, ul. Vavilova 30/6, Moscow, 117900, Russia

    A. V. Pechinkin & R. V. Razumchik

Authors
  1. A. V. Pechinkin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. V. Razumchik
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Original Russian Text © A.V. Pechinkin, R.V. Razumchik, 2013, published in Informatsionnye Protsessy, 2013, Vol. 13, No. 3, pp. 125–140.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pechinkin, A.V., Razumchik, R.V. Stationary characteristics of M 2|G|1|r system with hysteretic policy for arrival rate control. J. Commun. Technol. Electron. 58, 1282–1291 (2013). https://doi.org/10.1134/S1064226913120152

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1064226913120152

Keywords

Search

Navigation