A method of analysis of periodic processes in nonautonomous discrete-time systems with quantization

Abstract

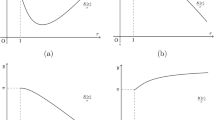
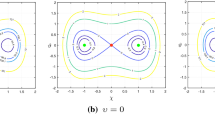
A method of analysis of stationary processes in systems with an arbitrary number of quantization levels in the presence of periodic external signals is proposed. The method is based on the representation of stationary oscillations in the form of an invariant set of nonlinear discrete point mappings. The spectral composition of the response of a system with an arbitrary period coupled with the discretization period through a rational relationship is calculated with the use of the discrete Fourier transform. The discrete Fourier transform is applied also to calculate nonlinear distortions. It is suggested to use the dependence of the ratio of the first-harmonic amplitude of the system’s steady-state response to the amplitude of the input-signal harmonic on the frequency of the input harmonic signal as the amplitude-frequency characteristic of a nonlinear system. In addition, it is suggested to use the dependence of the difference between the argument of the first harmonic of the system’s response and the initial phase of the input signal on the frequency of the input harmonic signal as the phase-frequency characteristic of the system. The usage of the method is illustrated by its application for the analysis of processes in first-and second-order circuits.