Abstract—
The paper presents a review of modern works on gasdynamic flow control using a highly nonequilibrium pulsed plasma. The main attention is paid to the effects based on ultrafast (on the nanosecond time scale for atmospheric pressure) local gas heating, since, at present, the main successes in controlling high-speed flows by means of gas discharges are associated with this thermal mechanism. Attention is paid to the physical mechanisms responsible for the interaction of the discharge with gas flows. The first part of the review outlines the most popular approaches for pulsed energy deposition in plasma aerodynamics: nanosecond surface barrier discharges, pulsed spark discharges, and femto- and nanosecond optical discharges. The mechanisms of ultrafast heating of air at high electric fields realized in these discharges, as well as during the decay of the discharge plasma, are analyzed separately. The second part of the review gives numerous examples of plasma-assisted control of gasdynamic flows. It considers control of the configuration of shock waves in front of a supersonic object, control of its trajectory, control of quasi-stationary separated flows and layers, control of a laminar–turbulent transition, and control of static and dynamic separation of the boundary layer at high angles of attack, as well as issues of the operation of plasma actuators in different weather conditions and the use of plasma for the de-icing of a flying object.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
NOTATION
x/c | dimensionless coordinate along the wing chord |
\(\bar {U}{\text{*}}\) | dimensionless averaged local velocity, \(\bar {U}{\text{/}}{{U}_{\infty }}\) |
\(F_{c}^{ + }\) | dimensionless excitation force frequency, Ff c/U∞ |
T* | dimensionless convection time, tU∞/c |
C P | pressure coefficient |
C L | lift coefficient |
C M | pitching moment coefficient |
C D | drag coefficient |
U | instantaneous local velocity |
V | discharge voltage |
n | gas density |
\({{n}_{i}}\) | ion density |
\({{n}_{e}}\) | electron density |
γ | specific heat ratio, \({{C}_{p}}{\text{/}}{{C}_{v}}\) |
E B | breakdown electric field |
E/n | reduced electric field |
k | pitch frequency, πfc/U∞ |
U S | speed of sound |
U ∞ | free stream flow velocity |
νc | frequency of transport collisions of electrons |
α | angle of attack |
\(\bar {U}\) | averaged local velocity |
c | wing chord |
F | frequency |
F f | excitation force frequency |
ω | laser frequency |
f | pitching frequency |
\({{\nu }_{\varepsilon }}\) | frequency of electron energy relaxation |
Ω | frequency of the electromagnetic field |
M | Mach number, U∞/US |
Rec | chord Reynolds number, \({{U}_{\infty }}c{\text{/}}\nu \) |
St | Strouhal number, Fc/U∞ |
E | electric field |
ωpe | electron plasma frequency |
ns-SDBD | nanosecond surface dielectric barrier discharge |
AC-SDBD | alternating current surface dielectric barrier discharge |
\({{T}_{e}}\) | effective electron temperature |
E eff | effective electric field |
1 INTRODUCTION
Active flow control using low-temperature plasma is currently a rapidly developing area of aerodynamics [1–3]. One of the main practical advantages of the effect of plasma on the flow is its fast response times. It can be effective in a wide range of frequencies and gasdynamic flows, from stationary flows to separated and turbulent flows [4]. Two other advantages of plasma systems are their low weight and size. In addition, they have relatively low power consumption. All this makes it possible to develop fundamentally new systems of flight control at high speeds.
The use of plasma systems in aerodynamics proves to be promising in controlling the laminar–turbulent transition in the boundary layer, controlling the separation of the flow or its reattachment to an airfoil surface, and changing the drag and lift of the wing. Also, with the help of plasma, significant progress can be achieved in such issues as affecting the noise characteristics and flow fluctuations, and control of the structure of shock waves and their interaction with the boundary layer. The devices used for plasma-assisted gasdynamic flow control are called plasma actuators.
One of the pioneering attempts to affect the flow by means of a nonequilibrium plasma was made more than 50 years ago [5, 6]. The authors of this work studied the control of flow separation by means of a surface barrier dielectric discharge with imposing a sinusoidal high-voltage pulse in the frequency range 50–570 Hz. The reduction in the drag force reached 30% and the increase in the lift force reached 40% in the range of the airfoil flow velocity from 8.75 to 20.4 m/s. It was concluded that the actuator affected the flow by means of the ionic wind when the velocity induced by it was 20–25% of the free flow velocity.
One of the first studies of the plasma effects on the shock wave propagation in a gas was made in [7]. The authors observed an increase in the velocity of a shock wave during its propagation in a gas discharge with a simultaneous decrease in the wave amplitude. The experimentally measured increase in the shock wave velocity was compared with the results of calculation taking into account the energy released in the discharge. The resulting difference (1200–1300 m/s instead of 900 m/s) was attributed to the possible h-eating of gas due to the quenching of vibrationally and electronically excited molecules and to the effect of the formation of a double layer in the shock front.
Several hypothetical schemes have been proposed to modify and control the flow around a supersonic object. These schemes used new approaches to plasma generation, magnetohydrodynamic (MHD) flow control and energy generation, hot gas counterflow, and other thermal effects [1].
A further increase in interest in plasma-assisted flow control dates back to 1993 and is connected with the work of Roth et al., who again used a surface discharge to control flow separation in the boundary layer. In [8–12], the possibility of suppressing the flow separation at low velocities using a dielectric surface RF discharge was demonstrated.
Another interesting experimental study was presented in [13]. Ballistic experiments were carried out to measure the drag force when a sphere with a diameter of 15 mm moves at a velocity of 200 to 1350 m/s in a nonequilibrium plasma created in air by an RF discharge. An anomalous stand-off distance increase of the shock wave from the sphere inside the discharge zone by distances significantly exceeding the sizes of thermal inhomogeneities at the entrance to the plasma was detected. Measurements of the drag coefficient indicate a significant reduction in drag at subsonic velocities and a slight increase at supersonic velocities. The decrease in the drag coefficient at subsonic velocities did not agree with its expected reduction at an experimentally observed increase in temperature and decrease in the Reynolds number. The authors showed that the observed effects are caused by the high speed of propagation of disturbances over the entire velocity field in the presence of plasma.
The possibilities of plasma-assisted flow control can be divided into two groups: (1) control of the main flow, including the configuration of the shock wave in supersonic and hypersonic regimes, and (2) control of the boundary layer. The main flow control includes the action on the shock-wave shape, aerodynamic deceleration, drag reduction, heat release reduction, changing the flow direction, the flow acceleration and deceleration, and MHD energy generation. The boundary layer control is subdivided into the control of the laminar–turbulent transition, the boundary layer separation, and the lift and drag forces, as well as the control of acoustic perturbations and increasing mixing efficiency.
There are three different physical mechanisms of the plasma effects on aerodynamics: (a) gas heating, (b) electrostatic transfer of momentum from charged particles to gas, and (c) magnetohydrodynamic effects, including MHD flow acceleration, and generation of electrical energy on board using the kinetic energy of the flow. Sometimes it is necessary to take into account the dissociation of the gas and the change in its mean molecular weight. However, significant dissociation or ionization of gas requires a large amount of energy. Therefore, in the aerospace industry, they try to keep the excitation of the gas at a minimum level, which reduces the role of effects associated with a change in the composition of the gas in the discharge.
Increased interest in plasma aerodynamics has led to a growing stream of publications in this area. In recent years, there have been many impressive demonstrations of the effects of plasma on gas flows. Some of them are reflected in thematic reviews published recently. For example, the possibilities of plasma control of supersonic flows (including damping of shock waves and changing their shape) were discussed in [1]. The advantages of plasma actuators over gas jet and mechanical actuators as applied to high-speed flow control are demonstrated in [14, 15]. A review of works on the effect of discharge plasma on gasdynamic flows using electrodynamic forces (ionic wind) is given in [2]. A reduction in the drag of a body at high flow velocities by means of energy deposition was considered in [16, 17]. A review of works on the control of flow separation in the boundary layer using a nonequilibrium plasma is given in [18–22]. The effect of pulsed heating on the interaction of shock waves with the boundary layer was studied in [23] for various methods of energy deposition. A review of methods for the excitation of gasdynamic instabilities by means of local pulsed heating is presented in [24, 25]. The kinetic processes that determine the interaction of nanosecond dielectric and quasi-stationary surface discharges with gasdynamic flows are considered in [26, 27]. Reviews [28, 29] include many new results obtained on the basis of various mechanisms (thermal, electrostatic, and magnetohydrodynamic), as well as a discussion of their applications for flow control in subsonic and supersonic regimes. However, a lot of time has passed since the publication of these reviews. New important results that clarify the mechanisms and the effect of plasma actuators on the flow have appeared. Therefore, in this review, we only briefly outline the most important results of plasma aerodynamics pertaining to the period up to 2010 and present in more detail the new works and data. The consideration is limited to the effect of a strongly nonequilibrium pulsed plasma on gasdynamic flows, which is based on ultrafast (on the nanosecond time scale for atmospheric pressure) local gas heating. The main successes in controlling high-speed plasma flows are currently associated with this effect. Much attention is paid to the physical mechanisms that facilitate or impede plasma-assisted gas flow control.
The first sections of the review are devoted to the most popular approaches in plasma aerodynamics to organizing pulsed energy deposition: nanosecond surface barrier discharges, pulsed spark discharges, and nanosecond optical discharges. The mechanisms of ultrafast heating of air at high electric fields realized in these discharges, as well as the processes that determine the decay of a strongly nonequilibrium discharge plasma, in which the air is significantly heated, are considered separately. The second part of the review gives examples of plasma-assisted control of gasdynamic flows due to pulsed heating of air. In this case, control of the configuration of shock waves in front of a supersonic object, control of its trajectory, control of quasi-stationary separated flows and layers, control of boundary layer separation at high angles of attack, control of dynamic flow separation, and the use of plasma for the de-icing of a flying object are considered.
2 NANOSECOND SURFACE BARRIER DISCHARGES
Nanosecond surface discharges were widely used in the second half of the last century to create preionization in electric-discharge excimer lasers [30]. In this case, the working medium was usually noble gases or their mixtures with halogen-containing compounds. Pioneering experiments studying the possibility of using nanosecond surface dielectric barrier discharges (ns-SDBD) to control flows in atmospheric-pressure air date back to the beginning of this century [31–33].
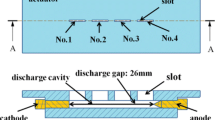
Figure 1 shows a typical schematics of electrodes and discharge gap used for SDBD-based plasma actuators [34]. Here, two flat electrodes are separated by a dielectric layer, which avoids conduction current from one electrode to the other. The high-voltage electrode is on top, and the second electrode is usually grounded. The discharge occurs at the edge of the high-voltage electrode after applying a voltage pulse to it.
Schematics of an SDBD discharge gap [34].
Figure 2 shows ICCD photographs illustrating the development of an SDBD discharge of both polarities in atmospheric-pressure air under the action of high-voltage pulses with an amplitude of 28 kV at the high-voltage electrode [32, 33, 35, 36]. The pulse half-width was 23 ns, and the rise and decay times were 8 and 15 ns, respectively. The repetition rate of the high-voltage pulse was 1 kHz. The low-voltage electrode was covered with a 0.4-mm-thick PVC film. The permittivity of the film was ε ≈ 2.7. The images of discharge development were obtained with nanosecond time resolution using an ICCD camera focused on the upper plane of the outer electrode and the dielectric layer.
Images of the development of a surface nanosecond barrier discharge with a nanosecond time resolution [36]. Exposure 0.5 ns. (a) Cathode-directed discharge and (b) anode-directed discharge.
The discharge developed from the edge of the high-voltage electrode over the low-voltage electrode covered with a dielectric layer. The propagation of a cathode-directed (positive) discharge was divided into four stages. At the first stage, the discharge developed over the grounded electrode (1, 3, and 4 ns; Fig. 2a). The discharge propagation velocity at this stage was approximately 1 mm/ns. Here one can observe the radiation of the entire streamer channel, not just the ionization wave front. When the length of the streamers exceeded the length of the lower electrode, their velocity decreased (to 0.3 mm/ns). This stage took 5 ns (6 and 10 ns, Fig. 2a). After this stage, the “dark” phase of the discharge began, when no discharge radiation was observed (from 13 to 20 ns, Fig. 2a). During the propagation of the streamers, the dielectric surface was charged. Thus, when the trailing edge of the high-voltage pulse reached the electrode, the potential of the electrode became lower than the potential of the dielectric surface in the discharge gap. This gave rise to the reverse discharge wave, which facilitated the charge removal from the surface (22 and 37 ns, Fig. 2a). The second flash is similar to the first one with the only difference that the discharge did not go beyond the low-voltage electrode, because, outside this region, there was no sufficient surface charge (34 and 37 ns, Fig. 2a).
The anode-directed (negative) discharge (Fig. 2b) developed in almost the same way as the cathode-directed one. The main difference is that the propagation velocity of the anode-directed discharge was lower. This led to a reduction in the dark phase (from 14 to 20 ns, Fig. 2b). When the streamers’ length exceeded the length of the lower electrode, the structure of the discharge was different from the case of a cathode-directed discharge (compare Fig. 2a at 6 ns and Fig. 2b at 14 ns). Here, the discharge distribution over the dielectric surface was more uniform and the streamers were less pronounced.
Currently, SDBD schemes have been proposed in which the development of a reverse breakdown wave is excluded [37–41], which may be important for more effective gas flow control. The reverse breakdown wave was suppressed in a nanosecond SDBD by means of a “diode” surface in the electrode circuits, which conducts current in only one direction.
From the above photographs, it follows that the discharge developing over the dielectric surface has two phases: forward and reverse waves, associated with the leading and trailing edges of the voltage pulse [32, 33, 35]. Although there is a certain similarity of the plasma filaments shown in Fig. 2 to the well-studied volume streamer discharge [42, 43], there is a fundamental difference between them. In a streamer discharge, the only emitting part is its “head,” where the region of a strong electric field is found, and the plasma channel with a weak electric field does not glow. A different situation is observed in SDBDs of any polarity, where not only the ionization front, but also the channels are glowing. The latter indirectly indicates the presence of a strong electric field also in the channels of such discharges, far behind the ionization front.
The strong effect of an SDBD on the gasdynamic flow is associated primarily with fast heating, which is determined by such characteristics as the energy deposition in the discharge and the efficiency and rate of energy transfer from the current carriers, electrons, to heat. The kinetics of gas heating is related to the degrees of freedom of molecules to transfer electron energy. In a weakly ionized nonequilibrium plasma, it is determined by the reduced electric field E/n (n is the number density of neutral particles), on which the mean electron energy in the discharge and all other electronic characteristics depend [42].
The parameter E/n was measured in SDBDs of different polarities by emission spectroscopy with respect to the emission intensity ratio of the first negative system of \({\text{N}}_{2}^{ + }\) ions (391.7 nm) and the second positive system of N2 molecules (337.1 nm) [32, 33, 44–46]. Figure 3 shows the results of such measurements [46] in the case of atmospheric-pressure air for single voltage pulses with a duration of 20 ns and a rise time of 0.5 ns. Since the radiation was collected from above the discharge (Fig. 1), the resulting electric field was averaged over the thickness of the plasma layer. Here, the maximum of the field was reached in the first 1–2 ns; then the field decreased and could have a second maximum of smaller amplitude. The electric field in the positive-polarity discharge was higher than in the case of negative polarity. The obtained maximum values of E/n are in good agreement with other similar measurements [32, 33, 44, 45]. The parameter E/n in an SDBD remained almost unchanged as the pressure decreased from atmospheric to 200 Torr [32, 33].
Time evolution of the electric field at different distances from the high-voltage electrode in atmospheric-pressure air at a voltage of (left column) +24 kV and (right column) –24 kV [46].
A disadvantage of this method is measurement error due to the strong inhomogeneity of the SDBD plasma. Here, radiation is usually collected above the dielectric surface from the entire surface layer, in which the plasma is created. This layer is highly i-nhomogeneous: the plasma parameters, including the electric field, can vary at distances of the order of 10–2 mm [47]. As a result, the radiation of the first negative system of \({\text{N}}_{2}^{ + }\) ions and the second positive system of N2 molecules can come from different parts of the layer. In this case, the reduced electric field reconstructed from the intensity ratio of these lines can be overestimated relative to the real values of the field in the plasma [46, 47].
Since recently, the electric field in a nanosecond SDBD is determined by laser methods. The measurements of the electric field are based on four-wave mixing [48] and generation of the second harmonic of picosecond Nd:YAG [49, 50] or femtosecond Ti-sapphire [51] lasers in an SDBD air plasma. These approaches made it possible to follow the dynamics of the electric field components at different points of the discharge gap. In this case, the electric field was averaged along the course of the laser beam, which was usually directed along the dielectric surface, perpendicularly to the direction of the discharge development. For example, Fig. 4 shows the dynamics of the electric field components measured in an SDBD plasma at a height of 100 μm above the dielectric [51]. The discharge was ignited in air at a pressure of 345 Torr under the action of high-voltage pulses with an amplitude of 20 kV and a pulse full width at half-maximum (FWHM) of 25 ns. The pulse repetition rate was 20 Hz. The time interval 0–5 ns in the figure corresponds to the situation when the ionization wave has not yet reached the observation point, at which the initial electric field, created by the residual surface charge on the dielectric after the previous pulse and the high-voltage electrode potential, is recorded. During the passage of the ionization wave (5–8 ns), the field increases and, at the maximum of E/n, reaches 700 Td (1 Td = 10–17 V cm2). After the departure of the ionization wave, a plasma is created at the observation point and the field during the voltage pulse is maintained at a level slightly below the breakdown threshold. With a decrease in the voltage at the electrode by the time t = 22–26 ns, the electric field also decreases. It starts to increase again at t > 30 ns, when the pulse ceases completely. This increase is associated with the creation of a reverse electric field from the charge accumulated in the gap. (This equipment does not measure the direction of the electric field.)
Time evolution of the longitudinal and transverse electric fields for an ns-SDBD in air at a pressure of 345 Torr [51]. The measurements were made at a point removed from the high-voltage electrode by a distance of ~2 mm and located at a height of 100 μm above the dielectric surface.
Thus, modern methods for measuring the electric field in an SDBD plasma make it possible to reproduce the main qualitative regularities of the discharge development, which were previously studied using high-speed imaging (see Fig. 2) and give the maximum values of electric fields, which qualitatively agree with previous measurements by emission spectroscopy (see Fig. 3). Note that field measurements by laser methods still raise many questions, in particular, due to the peculiarities of the calibration of such measurements, which presume significant extrapolation of the calibration dependences obtained in pre-breakdown fields to regimes in which the field exceeds the breakdown field by a factor of ten or more. Another difficult question is the averaging of the obtained values over the Rayleigh region of the beam. Therefore, these measurements should be considered only as a qualitative confirmation of the previous results.
The most important characteristic of the fast gas heating in an ns-SDBD is the dynamics of the gas temperature during the discharge and in its afterglow. The translational temperature of molecules in an ns-SDBD and its afterglow in atmospheric-pressure air was measured by emission spectroscopy using the emission from the second positive nitrogen system (337.1 nm) [44]. To measure the temperature, in this work, an additional high-voltage pulse was used, which illuminated the decaying plasma after a fixed time interval. Figure 5 shows the dependence of the gas temperature on the voltage during the discharge phase and 1 μs after it for discharges of different polarities. During the experiment, a 1-mm-wide diaphragm was installed so that discharge radiation from a 1-mm-wide region adjacent to the upper electrode was detected. In the case of a negative discharge, the temperature turned out to be somewhat higher both during the discharge phase and in the afterglow. With increasing voltage, the temperature increased in the case of both polarities of the discharge. From the data presented in Fig. 5, it follows that air at atmospheric pressure can be noticeably (by 150 K) heated already during the discharge stage for times of the order of 10 ns and that this heating increases significantly and reaches hundreds of degrees 1 μs after the pulse. A direct evidence of the fast heating in an SDBD plasma is also the formation of a shock wave. The propagation of this wave from the discharge region was detected in many experiments (see, e.g., [32, 33, 52]).
Temperature as a function of the voltage amplitude (1, 3) during the discharge and (2, 4) in the discharge afterglow after 1 μs for (1, 2) positive and (3, 4) negative polarities [44].
Systematic measurements of the ns-SDBD characteristics, including the limiting length and propagation velocity of the ionization wave, as well as the thickness of the plasma layer, were carried out by photographing the discharge with a short exposure using an ICCD camera in air at various pressures and a voltage pulse with a duration of 20 ns [53]. The discharge propagation length decreased from 50 to 5 mm as the pressure increased from 0.1 to 1 atm. In this case, the thickness of the plasma layer decreased from 1.5 to 0.2 mm. Thus, an increase in air pressure leads to a proportional decrease in the size of the plasma layer.
The SDBD characteristics depend not only on the gas pressure [54, 55] and the parameters of the high-voltage pulse, but also on the properties of the dielectric layer separating the electrodes. In [50, 56], it was experimentally studied how the variation in the thickness of the dielectric and its electrical parameters affects the characteristics of a discharge in atmospheric-pressure air, primarily, the limiting length of the discharge development. It turned out that an increase in the permittivity ε from 2 to 35 leads to a significant reduction in the discharge development length, while a change in the thickness of the dielectric layer from 0.8 to 35 mm had almost no effect on the discharge length [56]. In addition, the properties of a repetitively pulsed discharge depend on the charge relaxation rate on the dielectric surface. Due to a decrease in the residual charge effect in the case of using a dielectric with a short relaxation time (and with a decrease in the pulse repetition rate), the ionization waves during the discharge were more pronounced and were characterized by higher values of the maximum electric field and discharge current [50].
The form of development of a nanosecond SDBD shown in Fig. 2 was called quasi-homogeneous, in contrast to the form with pronounced plasma filaments observed at increased energy deposition and/or pressure [57, 58]. This shape of a discharge is typical not only of nanosecond pulses and was previously encountered when a high-frequency sinusoidal voltage was applied [47]. The effect of an SDBD on the gas dynamic flow depends on the regime in which the discharge develops. Therefore, the transition from a quasi-uniform discharge to a discharge with filaments is important in practical application. According to observations [58], filaments were formed a few nanoseconds after the onset of SDBD development and only at negative voltage polarity (Fig. 6). Figure 7 shows the boundary of air pressure and voltage amplitude where the filaments are formed and where the quasi-uniform discharge form is realized. A detailed review of the experiments studying this phenomenon in the nanosecond and other ranges of SDBD is given in [47].
Images of the development of a surface nanosecond barrier discharge in plane geometry with nanosecond time resolution [58]. Images taken at different air pressures and voltage amplitudes. Exposure of 0.5 ns and pulse duration at half maximum of 25 ns.
Regions of (under the curve) quasi-uniform discharge and (above the curve) discharge with filaments for an SDBD in air at negative polarity of the applied voltage [58].
In [59], the properties of plasma in SDBD filaments were studied using optical emission spectroscopy. It was shown that the radiation intensity in plasma filaments in air exceeds the SDBD radiation intensity about 50-fold. This radiation, forming a continuous spectrum, prevails in the ultraviolet range and noticeably decreases in the visible and infrared ranges. Further experimental studies of filaments in SDBD showed that they are characterized by higher (compared to discharge plasma without filaments) values of energy deposition, density, and mean electron energy [60]. Filamentization of the discharge leads to an increase in the energy deposited in one channel (the channel of the filament or streamer-like plasma formation at the transition stage) by an order of magnitude (Fig. 8). (A sharp increase in the energy deposition in the SDBD during filament formation was also indicated by measurements [48].)
Energy deposited in one SDBD plasma channel (streamer or filament) vs. air pressure [60]. Measurements for two voltages of negative polarity.
In this case, the specific energy deposition per particle is anomalously high (~7 eV), the electron density estimated from the Stark broadening of spectral lines and their temperature reach 5 × 1018 cm–3 and ~3 eV, respectively. The characteristic time of plasma decay is tens of nanoseconds. In [60], it is assumed that the filament plasma is in local thermodynamic equilibrium; therefore, its relatively slow decay is associated with the slow process of cooling the filaments. The main question concerns the mechanism of their formation. According to estimates [60], an important role in the development of filaments is played by stepwise ionization and dissociation of molecules by electron impact, as well as gas heating during electron–ion recombination. The filaments themselves are generated at the surface of the high-voltage electrode. Their generation mechanism is currently not clear. For example, with a negative voltage polarity, it can be caused by the field emission of electrons from the cathode surface. However, at present, there is still no clear physical picture of the phenomena leading to the formation of filaments in an SDBD.
Modeling the development of all structural elements of an SDBD is a nonstationary three-dimensional problem in which all parameters of the discharge plasma change abruptly on small time and space scales. At present, it is not possible to quantitatively describe all these phenomena on the basis of numerical physical approaches. Therefore, the main approach to modeling the development of an SDBD is based on the two-dimensional (2D) approximation, which takes into account the plasma inhomogeneity in the direction of the discharge development and in the direction perpendicular to the dielectric surface, while, in the third direction, the plasma is considered homogeneous [47, 64]. Thus, the development of a plane plasma sheet along the dielectric surface is considered, and the transverse structure of the discharge is neglected. The simulation is based on the numerical solution of a system of fluid equations for charged particles (within the drift-diffusion approximation) and Poisson’s equation for the electric potential, by analogy with modeling the development of a volume streamer discharge [43]. In this case, along with the traditional volumetric processes of the creation and destruction of charged particles, it is necessary to take into account the processes of photoemission from the surface, photoionization of gas, leading to the formation of seed electrons in neutral air, as well as the effects of nonlocality when describing the ionization of molecules by electron impact. The rest of the processes, including ion-molecular processes, are described at atmospheric pressure in the local approximation, when all the characteristics of charged particles are determined by the reduced electric field at a given point and at a given time. However, at low air pressures, nonlocal effects can also become important for these processes [61]. To obtain quantitative characteristics that are of greatest interest in plasma aerodynamics, it is necessary to self-consistently simulate the development of an SDBD and the gasdynamic perturbations produced by it [62].
The following qualitative picture of the development of SDBD in air is obtained from numerical two-dimensional modeling [47, 64]. With a positive-polarity voltage at the high-voltage electrode, the discharge develops in the form of a flat streamer, in which the main ionization occurs in the leading edge. In the case of negative-polarity voltage, the main ionization takes place in the cathode layer near the edge of the high-voltage electrode and the discharge is a special form of a nonstationary glow discharge. In this case, the negative discharge is more homogeneous and diffuse in comparison with the positive discharge, in which a strong longitudinal plasma inhomogeneity is present at the leading edge of the ionization wave.
Two-dimensional modeling of SDBD makes it possible to obtain reasonable agreement between experimental data and calculations for integral discharge characteristics: the limiting length of the discharge development [62, 63], discharge current [62], and energy deposition [64]. Attempts to compare the calculation with experiment for more detailed characteristics of the discharge—the time evolution of radiation from the discharge plasma—turn out to be less successful [63]. This may indicate the imperfection of the two-dimensional SDBD models, as well as the neglect in the calculations of some important effects, in particular, photoemission from the dielectric surface and the accumulation of surface charge from previous discharge pulses.
In [33, 65], three-dimensional numerical simulation of the SDBD development was attempted. However, these attempts should be recognized as unsuccessful, since too coarse computational grids were used, which did not allow obtaining adequate quantitative characteristics of the discharge. Also, based on the results of two-dimensional modeling of the SDBD, an approximate analytical model of the discharge was proposed [66] to explain the processes occurring in the plasma at a qualitative level. This model made it possible to obtain analytical dependences of the propagation velocity and the length of the discharge zone on the parameters of the dielectric layer and the applied voltage in the case of a single pulse.
3 PULSED SPARK DISCHARGES WITH FAST HEATING OF GAS
To prevent the transition of a glow discharge and some other types of gas discharge into an arc, they usually try to limit the discharge current by including high resistances or dielectric layers in the electrical circuit. Maintaining a plasma in atmospheric-pressure air without arc formation was also possible in a high-voltage nanosecond repetitively pulsed discharge [67, 68]. Such a discharge develops in a strong electric field, creating a strongly nonequilibrium plasma, and the arc does not have time to form due to the short duration of the voltage pulse. In this case, active ionization takes place in each pulse in a strong electric field, and a large number of metastable particles, which facilitate the maintenance of the discharge, are produced. In addition, the gas heats up quickly, which is important for flow control.
In [67], using as an example a discharge in a 1.5‑mm gap it was experimentally shown that applying voltage pulses with a duration of 10 ns, an amplitude V = 5 kV, and a pulse repetition rate of 30 kHz made it possible to ignite a repetitively pulsed discharge in air under normal conditions. In the first few pulses, its characteristics were close to a pulsed streamer corona, but then a regime was established in which the discharge current sharply increased to 100–150 A, the energy deposition in one pulse increased to 2 mJ, and the gas temperature increased to 3000 K. Estimates showed that the discharge development occurred at high values of E/n, when the fast gas heating is especially effective. Such a discharge development regime can be classified as a nanosecond spark.
In air heated to 2000 K [68] and 1000 K [69], a new regime of maintaining a nanosecond repetitively pulsed discharge was also observed, which was called a glow regime. Figure 9 shows photographs of various forms of a nanosecond discharge: corona, glowing mode, and spark, when a repetitively pulsed voltage V with a frequency f = 10 kHz, a duration of 10 ns, and a voltage rise and fall time of ~5 ns was applied to the gap of length d = 4.5 mm between point electrodes [69]. The discharge was ignited in atmospheric-pressure air at a gas temperature T = 1000 K. The succession of different modes with increasing voltage V resembles the corona–glow discharge–arc sequence in the case of a DC discharge [42]. When applying a nanosecond discharge with V increasing from 5 to 6 kV, a transition occurred from the corona to the glow mode, later replaced with a spark. In all modes of the nanosecond discharge, radiation in the air plasma was dominated by the second positive nitrogen system, which indicates high values of the reduced electric field E/n in the discharge plasma. In the corona, radiation was present only at the anode. In the glow mode, the radiation became diffuse and occupied the entire gap. Finally, in the spark, the radiation intensity increased sharply, as well as the discharge current, which was ~1 A for the corona and the glow regime and increased to 20–40 A in the case of a spark. The energy deposition in the pulse also increased: it was less than 1 µJ in the corona, 1–10 µJ in the glow mode, and 200 µJ–1 mJ in the spark [69]. Since the parameter E/n was large in all regimes (~150–600 Td), the heating also became noticeable: according to emission spectroscopy measurements, it was ~200 K in the first two regimes and reached 2000–4000 K in the spark. The presence of high fields was evidenced by the observed high emission intensity of the second positive band of N2 and the first negative band of \({\text{N}}_{2}^{ + }\). The mechanisms of fast heating in such strong fields are the same as those considered in Section 6. With such parameters E/n, one of the main channels for the heating of air is the release of energy during quenching of the triplet states N2(A, B, C) by the O2 molecules.
Photographs of a nanosecond repetitively pulsed discharge (corona, glow discharge, spark) in air at atmospheric pressure, T = 1000 K and frequency f = 10 kHz [69]. The length of the discharge gap is d = 4.5 mm. The anode and cathode are labeled A and C, respectively. Gap voltage of (left to right) 5, 5.5, and 6 kV.
The electron density in the discharge plasma was ~1013 cm–3 in the glow mode and reached 1015 cm–3 in the spark [70]. That is why the spark was characterized by a much higher emission intensity than in the glow discharge regime. The emitting radius of the plasma channel in both cases was ~1 mm. In the case of a spark, the current density reached 1 kA cm–2, which is comparable to the corresponding values for a DC arc discharge [42].
In the glow mode, a cathode-directed streamer from the anode first developed. After closing the gap, it caused a reverse potential wave, which equalized the electric field in the discharge gap [69]. The voltage was switched off even before the formation of the cathode layer in it, which fundamentally distinguishes this discharge from a DC glow discharge. A different situation was observed in a nanosecond spark [70]. Here, as follows from the analysis of optical observations, the discharge developed uniformly, due to avalanche ionization in the volume. This breakdown mechanism is fundamentally different from the development of a conventional spark initiated by a single voltage pulse in atmospheric-pressure air, where the spark channel is usually formed after the gap is closed by a streamer discharge developing from one of the electrodes [43]. The possibility of uniform development of a nanosecond spark at a repetitively pulsed voltage is associated with the high (~1011 cm–3) density of seed electrons, which remain from the previous pulse to the beginning of the next pulse. Optical measurements showed that heating by several thousand degrees is carried out in the spark mode of a nanosecond repetitively pulsed discharge in air in a very short time of ~30 ns [70], which may be important for flow control using a nanosecond-discharge plasma.
In [71], the conditions for the transition between different modes of a nanosecond repetitively pulsed discharge in heated air at atmospheric pressure were studied in detail. The experimentally determined regions of realization of different discharge modes, depending on the amplitude and frequency of the applied voltage, are shown in Fig. 10 for T = 1000 K and an interelectrode gap of length d = 5 mm. A reduction in the pulse repetition rate from 30 to 1 kHz slightly expands and shifts the regions of existence of the corona and the glow regime to higher voltages.
Regions of different modes of a nanosecond repetitively pulsed discharge in the “voltage–pulse frequency” plane for atmospheric-pressure air at T = 1000 K and d = 5 mm [71]: (S) spark, (G) glow discharge, (C) corona, and (N) no discharge.
In [71], along with the frequency and amplitude of voltage pulses, the values of T and d were also varied. Figure 11 shows the regions of realization of different discharge modes, depending on the voltage and gas temperature, for f = 30 kHz and d = 5 mm. With decreasing T, the voltages necessary to ignite a corona increase due to the increase in the gas density at constant pressure. It is important that, below 650 K, under the conditions under consideration, only a corona and a spark can exist and the glow mode is observed only at T > 650 K. The variation of d at T = 1000 K and f = 30 kHz showed that the glow mode can be obtained only in a range 3 < d < 9 mm. For other gap lengths, only a corona and a spark were observed. An important question is whether it is possible to obtain a glow mode at room temperature. Analytical estimates [71] showed that one can expect a positive answer to this question with an increase in the duration of the high-voltage pulse and/or with a decrease in the radius of curvature at the ends of the electrodes.
Regions of different modes of a nanosecond repetitively pulsed discharge in the “voltage–gas temperature” plane for atmospheric-pressure air at f = 30 kHz and d = 5 mm [71]: (S) spark, (G) glow discharge, (C) corona, and (N) no discharge.
Subsequent experimental studies of a nanosecond repetitively pulsed discharge in air made it possible to determine the characteristics of the generated plasma in the temperature range T = 300–1000 K [72, 73], including the degree of dissociation of O2 (which reached 50%), the density of electronically excited N2 molecules, and the gas heating dynamics. The studies were carried out in the nanosecond spark mode. From the data on the dynamics of heating and on the energy deposition in the discharge, information on the fraction of energy rapidly transferred to heat in an air plasma at various values of the parameter E/n was extracted (see Section 6).
For the first time, a numerical study of a nanosecond repetitively pulsed discharge in air was carried out within a 1D model [74]. The calculations were performed for the experimental conditions [67], when a nanosecond spark developed in air under normal conditions (1 atm, T = 300 K). The results obtained were in qualitative agreement with the experiment, making it possible to determine the main mechanisms of the development and maintenance of the discharge, as well as the gas heating mechanisms. It was shown that the main role in the discharge processes was played by the fast gas heating in a strong electric field (E/n = 150–300 Td), associated primarily with the quenching of electronically excited states of N2 on O2. As a result, due to a decrease in n between pulses, the reduced field E/n increased during the voltage pulse, causing an increase in the ionization rate, further heating of the gas, and the transition of the discharge to the spark mode.
In [72], a 2D parametric numerical simulation of a nanosecond repetitively pulsed discharge was performed for conditions similar to those of experiment in [70]. The main attention was paid to the glow mode, and it was shown that it is realized only if the duration of the voltage pulse very slightly exceeds the time of closing the gap by the streamer discharge. Otherwise, in the stage after covering the gap, strong energy release and gas heating in the channel take place, leading to the transition of the discharge into a spark. This can be easily achieved in a 5-mm gap at T = 1000 K and difficult at room temperature, which agrees with observations [70]. Simulation in [73] of the successive development of several discharge pulses in a glow mode for air at atmospheric pressure and T = 1000 K showed that the discharge reached a quasi-stationary level corresponding to that observed in experiments with a nanosecond repetitively pulsed discharge. In this case, for the development of subsequent pulses, the density of charged particles remaining after the decay of the plasma by the time of the beginning of the next pulse is important. In a hot gas, it was higher due to the slowing down of the plasma decay with increasing T, which facilitated the discharge development.
Another type of pulsed spark discharge is a pulsed arc, on the basis of which the Localized Arc Filament Plasma Actuator (LAFPA) was created. This type of discharge, in contrast to a nanosecond repetitively pulsed discharge, on the one hand, has found wide application in plasma aerodynamics [23–25] and, on the other hand, it has been very little studied with respect to the mechanisms of its development. The use of this type of discharge for gasdynamic flow control was first proposed in [75]. The discharge was created in air between two electrodes placed at a distance of several millimeters by applying a repetitively pulsed voltage with a frequency of 10–300 Hz and a pulse duration of 1 μs to 1 ms. To prevent the plasma from being carried away by the high-speed flow, a groove on the surface of the body in the flow was created, along which the discharge developed. First, after applying the voltage, a breakdown in the gap occurred and a spark was formed. After the breakdown, a sharp decrease in the voltage across the gap to several hundred volts occurred, and this voltage was maintained until the end of the pulse. In this case, the electric field in the channel was significantly lower than the breakdown field, and the gas was heated to temperatures of 1000–2500 K. All this indicates that, in the main stage, the discharge was maintained in the form of a pulsed arc. The main property of the discharge, which turned out to be most valuable for the gasdynamic flow control, was the fast gas heating. Such heating occurred precisely during the breakdown of the discharge gap at the stage of a nanosecond spark [23], when the electric field was characterized by high values of E/n. In this case, the mechanism of fast heating was determined by the processes described in Section 6 (primarily by the energy release upon quenching of the excited states of N2(A, B, C) on O2 molecules). Gasdynamic perturbations created during the fast local heating of the gas are used to affect the gas flow. Thus, although this spark discharge noticeably differs from the nanosecond repetitively pulsed discharge described above, they are similar in relation to the processes of fast heating of gas.
Another type of spark discharge used for gasdynamic flow control due to the fast local heating of atmospheric-pressure air is a filamented pulsed microwave discharge [17, 23]. It has the shape of a “clue” of plasma filaments, in which the gas temperature rises to several thousand degrees in times lying in the nanosecond range [76–78]. The fast heating of the gas in the filaments causes gasdynamic perturbations such as weak shock waves, which can affect the characteristics of the gas flow. The mechanism of fast heating of gas in such a plasma does not differ from the corresponding mechanisms in the discharges described above and analyzed in Section 6. The difference between a microwave discharge (as like as an optical discharge) and other types of discharge used for pulsed heating of gas is that it allows heating remotely, in an electrodeless mode, at a considerable distance from the electromagnetic wave source.
Thus, using the pulsed spark discharges described in this section in atmospheric-pressure air, it is possible to create plasma in small volumes at high reduced electric fields E/n and to organize in it fast gas heating. This results in the generation of gasdynamic perturbations, which can be used to affect the main flow.
4 PULSED NANOSECOND OPTICAL DISCHARGES
Compared to other methods of energy deposition in a gas, a laser beam has a number of advantages. It is an electrodeless method of energy deposition, which makes it possible to achieve high values of specific energy deposition in the right place. When focusing a laser beam, the gas is ionized and a spark is formed, which has been demonstrated in a wide wavelength range with various lasers (CO2 and excimer gas lasers, solid-state ruby and neodymium lasers) [79–81].
The formation of a laser spark, leading to the absorption of the laser beam energy in the gas, occurs when the beam is focused in a small focal volume. The process develops through the following successive stages (Fig. 12): the appearance of the first electrons as a result of multiphoton ionization, avalanche ionization of the gas in the focal region, absorption of laser energy by a gaseous plasma, rapid expansion of the plasma, the formation of a shock wave, and its propagation into the surrounding gas [79–81].
Processes during optical breakdown of gas by laser radiation [82].
There are two mechanisms for the multiplication of electrons in a gas under the action of laser radiation. The first mechanism is multiphoton ionization, in which a neutral particle simultaneously absorbs a sufficient number m of photons for ionization. This process is written in the form
where M is a neutral particle, hν is a quantum of light, and mhν is the energy absorbed in this process. Upon ionization, the absorbed energy must exceed the ionization potential: mhν > I. In the process under consideration, the electron density increases linearly with time. The ionization potential of molecules in air is higher than 12 eV, and the quanta of the visible and near-IR ranges are usually on the order of or less than 1 eV. Therefore, the ionization of molecules in a laser beam must be multiphotonic.
The second ionization mechanism is based on the absorption of laser radiation by free electrons in the processes of inverse bremsstrahlung scattering. These processes are the reverse of the bremsstrahlung emission of light quanta during the scattering of high-energy electrons by neutral particles. If electrons acquire an energy exceeding the ionization potential of neutral particles, then collisions between them can lead to impact ionization:
This process causes avalanche ionization, in which the electron density increases exponentially in time, because all new electrons also heat up and begin to participate in ionization collisions.
With the development of avalanche ionization, the forming plasma begins to efficiently absorb the energy of the laser beam. First, avalanche ionization takes place in the small focal region with the maximum emission intensity (Fig. 12). But the absorption of laser radiation is not limited to the focal region, where the primary avalanche ionization occurs. When the degree of ionization in the plasma reaches a large value, avalanche ionization also begins in the regions with lower emission intensity, adjacent to the plasma region. The new region becomes ionized and, ceasing to be transparent to radiation, begins to absorb its energy. Thus, the absorbing region is continuously displaced towards the laser beam, creating a gas heating wave. Thermal radiation from a highly heated region is absorbed by cold gas, which, in turn, begins to emit light [79]. This process is called the radiative ionization wave propagation mechanism, which results in the distribution of laser energy over a large region, which lowers the maximum temperature in the gas. In addition to the thermal radiation of the plasma, there are other mechanisms that lead to the ionization of the gas in the layers adjacent to the already formed plasma. These are molecular thermal conduction and gas heating by a shock wave. These mechanisms of plasma propagation can be realized in various combinations, depending on specific conditions [79].
At the final stage of energy absorption, the laser pulse terminates and the plasma decays due to electron–ion recombination. The focal region and adjacent regions prove to be significantly heated. Here, the pressure sharply increases, which leads to a decrease in the gas density during the propagation of the shock wave and rarefaction waves. Subsequently, at the place where the optical breakdown occurred, a toroidal vortex can form, which creates a gas flow in the direction of the laser beam propagation.
The threshold for the breakdown of gases by laser radiation depends on many parameters [79–81]: characteristics of the gas medium (composition of the gas, its pressure, the presence of impurities, including aerosol and solid microparticles), radiation characteristics (wavelength, pulse duration), and the size of the focal region. For example, Fig. 13 presents the results of measuring the threshold electric field EB for breakdown in air in a wide range of pressure under the action of UV radiation (193 nm, ArF laser, pulse duration of 20 ns) [83] and IR radiation (1064 nm, Nd:YAG laser, pulse duration of 6 ns) [84]. The figure also shows the effective field
which characterizes the efficiency of electron heating in an alternating electric field. Here, νc is the transport frequency of collisions of electrons with other particles (neutrals and ions) and ω is the frequency of the electromagnetic field. Under these conditions, \(\omega \gg {{\nu }_{{\text{c}}}}\) and Eeff ≈ EBνc/ω. As follows from Fig. 13, the breakdown threshold increases with decreasing pressure and emission wavelength. The high breakdown thresholds at low pressures are explained by the small number of collisions of electrons with neutrals in this case [79]. Here, for the ionization of molecules, electrons must be heated by a laser field to the ionization threshold, while electrons are heated because of collisions (reverse bremsstrahlung).
A reduction in the wavelength by an order of magnitude leads to an increase in the breakdown threshold about 10-fold. At the same time, the field Eeff turns out to be almost independent of the radiation wavelength. Hence, the increase in the threshold field EB with decreasing wavelength is associated with less efficient heating of electrons in the laser field at higher frequencies. The dependences of the threshold for the breakdown in air on other characteristics of the gas and the laser beam, their physical explanation, and a description of theoretical approaches to numerical simulation can be found in [79–81].
Figure 14 shows photographs demonstrating the development of the processes during laser breakdown in atmospheric-pressure air. The breakdown was carried out under the action of an ArF laser (193 nm) with an energy of 135 mJ and a pulse length of 20 ns. The photographs were taken with an ICCD camera (exposure of 10 ns) under illumination of the object with a CW laser. The direction of propagation of the laser beam in the figure is from left to right. The time reference point corresponded to the beginning of the laser pulse. Immediately after the breakdown (t < 25 ns), intense bremsstrahlung from the plasma was observed. At early times (t ≤ 100 ns), the heated region expanded from the focal region, as a result of which the plasma acquired a shape slightly elongated along the propagation of the laser beam. At times of the order of 1 μs, the shock wave separated from the heated plasma core and then expanded separately. The shock wave propagation was observed at times up to 60 μs, after which this wave weakened and went beyond the observation region. Around the same time, a significant deformation of the emitting plasma region occurred. Hence, we can conclude that the fast gas motion played an important role in the stability of the expanding heated plasma core. When the wave was far enough from the plasma core, colder air penetrated into the heated core in the direction of the laser beam propagation. Further expansion of the plasma region led, at times on the order of 2 ms, to the formation of a toroidal vortex-type structure. Such evolution of the plasma region and the gas jet created by it during the development in the gas flow can have a significant effect on its characteristics.
Dynamics of plasma produced in air by a laser beam with an energy of 135 mJ [83]. The size of each image is 1.3 × 1.3 cm2.
The formation of a laser spark in the gas and the gasdynamic phenomena caused by it are a complex combination of various physical processes, leading to the generation of fully or partially ionized equilibrium plasma at nanosecond times with a temperature in the range of 104–105 K [79–81]. Their theoretical description is usually limited to considering one or two stages of the formation of a laser spark, while the remaining stages are either not considered or are taken into account in a very simplified form. For example, the gasdynamic effects caused by the energy deposition from a laser spark in an air flow are often simulated under the assumption of an ultrafast distributed energy deposition in a given volume of gas [17].
The energy of laser radiation can be introduced into the gas not only in one pulse, but also in a more complex way. In [85, 86], a new concept of laser energy deposition was proposed, which consists in combining two laser pulses, one in the UV range (266 nm) and the other in the near IR range (1064 nm). This made it possible to avoid optical breakdown by simultaneously controlling both the energy deposition and gas heating. Here, primary electrons were created due to multiphoton ionization in the field of a UV pulse. After that, with a specified (~10 ns) delay, an IR pulse was applied, in which the electrons were heated so as to ensure avalanche ionization of the gas. The plasma created by a double laser pulse turns out to be nonequilibrium and requires much less energy for its creation than in the case of generation of an equilibrium plasma by a single laser pulse. In addition, the use of two laser pulses makes it possible to effectively control the plasma density and gas heating. For example, in a conventional laser breakdown of air, a single laser pulse produces a fully ionized plasma with a temperature exceeding 10 000 K [87, 88]. The use of two pulses in the UV and IR ranges makes it possible to create plasma with various (10–4–10–2) degrees of ionization and in a wide (400–10 000 K) temperature range [88]. The ability to control the energy deposition can be especially valuable in gas flow control problems. In addition, this approach turned out to be in demand for plasma-stimulated ignition and combustion [86, 89].
In connection with the progress in the development of femtosecond lasers [90], proposals have also appeared recently to affect the supersonic flow using thin plasma filaments formed during air breakdown under the action of terawatt laser radiation of femtosecond duration [91]. In this case, a highly nonequilibrium plasma of high (~1017 cm–3) density is created, during the decay of which, in the nanosecond range, pulsed heating of the gas occurs [92].
5 DECAY OF NON-EQUILIBRIUM AIR PLASMA
At high reduced electric fields E/n, a significant part of the energy deposited in the discharge is spent on gas ionization. This channel of energy transfer from electrons becomes the main one at E/n ~ 1000 Td and higher. During plasma decay, charged particles recombine in the afterglow of a nanosecond discharge. As a result, significant energy is released, some of which goes into heat. To quantitatively describe this process, which leads to fast heating of gas, it is necessary to have an idea of collisional processes, due to which the air plasma decays [93, 94].
In a nanosecond discharge in air during a high-voltage pulse, electron impact ionization of molecules produces only primary ions. In the case of dry air, these are \({\text{N}}_{2}^{ + }\) and \({\text{O}}_{2}^{ + }\) ions, and, in humid air, Н2О+ ions are added. Primary ions enter into ionic-molecular reactions, which lead to the formation of new ions. This occurs during plasma decay, and, if the gas pressure is high enough, it can also occur during a nanosecond discharge. At the discharge stage, all charged particles are heated in a strong electric field. The mean electron energy is much higher than the mean ion energy. For example, in an air plasma at E/n = 200 Td, the mean electron energy is εe ~ 6 eV [42] and the mean ion energy is εi ~ 1 eV [61]. In this case, the both electron and ion energy distributions in a weakly ionized plasma are nonequilibrium.
After turning off the electric field, when the plasma decays, the charged particles also begin to cool and their mean energy tends to the mean energy of neutral particles and the energy distributions tend to the equilibrium Maxwellian distribution. Ions in air cool much faster than electrons, because, for ions, unlike electrons, each elastic collision with a neutral particle leads to a strong decrease in kinetic energy. At atmospheric pressure, the characteristic relaxation time of the average ion energy in air is fractions of a nanosecond [61]. The relaxation time of the average electron energy is much longer. It is important that the cooling of electrons is also influenced by the electron–ion recombination processes due to the so-called recombination heating effect [95]. Since the processes of relaxation of the energy of electrons and their density are interrelated, in the general case, their modeling should be performed in a self-consistent manner. The processes of electron–ion recombination are nonthreshold, and the recombination coefficients are usually power functions of the effective electron temperature Те = 2/3εe. Therefore, in a theoretical study of plasma decay, it is usually sufficient to follow the relaxation of Те and there is no need to numerically simulate the relaxation of the electron energy distribution.
Under conditions typical of plasma aerodynamics, the decay of a strongly nonequilibrium weakly ionized air plasma occurs at pressures on the order of atmospheric pressure from the initial electron densities in the range 1014–1015 cm–3. It is difficult to study plasma decay under such conditions experimentally, since the discharge plasma, as a rule, is highly inhomogeneous and the most interesting are the nanosecond and microsecond time ranges. Here, standard approaches to measuring plasma density such as probe or microwave are of little use. An experimental study of air plasma decay after a high-voltage discharge at low pressures (1–10 Torr), where the discharge develops uniformly, can be considered as a possible approach. The development of kinetic schemes for the processes that determine plasma decay under these conditions and their validation with experimental data allow using these schemes to numerically simulate the properties of decaying plasma at increased air pressures, which is important for practice. It is important that the specific energy deposition in the high-voltage discharge is small enough. In this case, the generation of charged particles is not accompanied by the production of a large number of excited particles, which can strongly affect the kinetics of plasma decay. The fulfillment of this condition greatly simplifies the theoretical analysis of experimental data. It is these conditions that were realized, e.g., in experiments [96, 97], where the dynamics of changes in the electron density during plasma decay in air (1–10 Torr) after a high-voltage nanosecond discharge with a specific energy deposition of 0.002–0.02 eV/mol was studied using microwave interferometry. Numerical simulation [96, 97] showed that plasma decay under these conditions can be described on the basis of a fairly simple kinetic scheme, in which the main channel for the loss of charged particles is electron–ion recombination with positive ions, including cluster ions formed in the discharge afterglow.
In the literature, there are detailed kinetic schemes that make it possible to describe the loss of charged particles and ion-molecular processes during plasma decay in dry and humid air [98–104]. Modern data on the coefficients of dissociative electron–ion recombination, which is usually the main channel for the loss of charged particles under the conditions under consideration, are given in [105].
Analysis of the available data on the rate constants of elementary processes indicates the following features that should be taken into account when simulating the decay of a high-voltage nanosecond discharge plasma in atmospheric-pressure air.
1. Since the electron–ion recombination rate coefficients depend on the effective electron temperature, it is necessary to self-consistently simulate the loss of charged particles and the relaxation of the average electron energy after the termination of the discharge during their collisions with molecules.
2. The electron–ion recombination rate coefficient for cluster ions is an order of magnitude higher than for simple molecular ions. Therefore, it is necessary to take into account the formation of cluster ions during plasma decay and the recombination of electrons with these ions.
3. The formation of cluster ions is a three-body process, the rate of which is proportional to n2 in the limit of low gas pressures and proportional to n in the high-pressure limit. At atmospheric pressure, for the formation of cluster nitrogen and oxygen ions, a low-pressure regime is realized, and the formation of H3O+(H2O)k hydrated ions is close to a high-pressure regime [102, 104].
4. In the case of H3O+(H2O)k hydrated ions (dominant positive ions in plasma decay in humid air), there are two types of experiments to measure the recombination rate coefficients, which give very (up to an order of magnitude) different results. These are direct measurements of the recombination rate coefficients from the decay rate of a plasma with hydrated ions at not too low (>1 Torr) pressures [106–109] and experiments at anomalously low (10–11 Torr) pressures in ion accumulation rings [110–112], where the recombination cross sections are measured and the recombination coefficients are obtained by integrating the cross sections over the electron energy distribution. There is no doubt about the reliability of both types of measurements. At present, there is only one explanation for this difference: it is assumed that the dissociative recombination of electrons with hydrated ions occurs by different mechanisms at very low and increased pressures [113]. Hence a practical conclusion follows from [113]: when simulating plasma decay in humid atmospheric-pressure air, it is necessary to use the recombination coefficients for hydrated ions obtained and verified in [106–109].
5. At a sufficiently high (>1012 cm–3) electron density and not-too-high electron temperature Те, the process of three-body electron-ion recombination with a third body, an electron, becomes important. This process has been well studied for atomic ions [114, 115] and has hardly been studied for molecular ions. At the same time, it was suggested that the rate of three-body recombination for molecular ions (in particular, for \({\text{O}}_{2}^{ + }\) ions [96, 97, 116]) can be much higher than for atomic ions and that, in these cases, there are different dependences of the recombination rate coefficients on Те.
To illustrate the features of the decay of a high-voltage discharge plasma, Figs. 15 and 16 show the results of numerical zero-dimensional modeling of the evolution of the effective electron temperature and the charged particle densities in the afterglow of a discharge in dry and humid air at atmospheric pressure. The kinetic scheme of collisional processes describing plasma decay in this case is taken from [96, 97, 109]. In this case, the above-described specificities in collisional processes were taken into account. As in [96, 97, 109], it was assumed that the plasma is homogeneous and that the energy deposition in the discharge is so small that the influence of excited particles on the kinetics of plasma decay can be neglected. It was assumed that the electric field in the end of the discharge disappears at times much shorter than the relaxation time of Те and the plasma density. The calculations were performed at an initial electron density ne(0) = 1015 cm–3 (typical values for high-voltage nanosecond SDBD discharges) and Т = 300 K.
The dynamics of relaxation of the effective electron temperature in atmospheric-pressure air: (1) dry air, Те(0) = 1 eV, without recombination heating; (2) dry air, Те(0) = 10 eV, without recombination heating; (3) dry air, Те(0) = 1 eV, with recombination heating at I = 0; (4) dry air, Те(0) = 1 eV, with recombination heating at I = 0.136 eV; (5) air with 2% H2O, Те(0) = 1 eV, without recombination heating. The calculations were made for ne(0) = 1015 cm–3.
The relaxation of Те during plasma decay was simulated based on the numerical solution of the equation [95–97]
together with the balance equations for electrons and ions in the zero-dimensional approximation. Here, νε is the relaxation frequency of the electron energy in collisions with molecules, ni is the ion density, k3 is the coefficient of three-body electron–ion recombination, k2 is the coefficient of binary dissociative recombination of electrons with ions, and I is the energy acquired by free electrons upon three-body electron–ion recombination. Equation (1) is written for the case of one species of positive ions. If there are many of them, the summation is performed over the corresponding terms on the right-hand side of (1). The value of I was set equal to 0.136 eV [117]. The frequencies νε for О2, N2, and Н2О, used in the calculation, were taken from [109]. It was assumed that, due to the low energy deposition to the discharge, the vibrational excitation of the molecules is small. If this is not the case, then it is necessary to take into account in Eq. (1) the energy transfer between electrons and vibrational degrees of freedom of molecules, which can lead to additional heating of electrons in the afterglow of the discharge [118, 119].
The second and third terms on the right side of (1) describe recombination heating, which is caused by the following. First, in dissociative and three-body electron–ion recombination, electrons with lower energy react more efficiently. As a result, due to the loss of “cold” electrons, the average electron energy increases, which characterizes the second term on the right-hand side of (1). Second, in three-body electron–ion recombination, part of the energy released during this process is transferred to free electrons, heating them (the third term on the right-hand side of (1)).
Figure 15 shows the results of calculating the time evolution of the effective electron temperature Те in atmospheric-pressure air. Since the initial values of Те in a high-voltage discharge can vary over a wide range, the calculations were performed for Те(0) = 1 and 10 eV. As follows from the figure, the value of Те(0) is important only in the initial time interval (t < 0.05 ns) and further cooling of electrons does not depend on how hot they are in the beginning. The reason is that, at high energies, the relaxation of electrons is determined by their inelastic collisions with the excitation of electronic states of molecules for which the frequencies νε are high. These processes are efficient in cooling the electrons. At lower energies, vibrational and rotational excitation of molecules by electron impact becomes dominant, in which the cooling of electrons in collisions with N2 and O2 is not so effective. Therefore, the main time for cooling electrons to room temperature is determined precisely by the relaxation of low-energy electrons.
As follows from Fig. 15, in dry air, the relaxation time of Те is 10 ns, if the recombination heating is not taken into account. If this effect is considered, the relaxation of Те slows down significantly at Те < 3000 K, when the first term on the right-hand side of Eq. (1) decreases sharply due to a decrease in the frequency νε. As a result, the time of complete thermalization of electrons, when Те = Т, increases and reaches 30 ns, which is several times longer than the thermalization time in the absence of recombination heating. In humid air, the relaxation rate of the electron energy increases significantly at Те < 3000 K due to the effective vibrational and rotational excitation of the electron impact of H2O molecules with a large constant dipole moment. This leads to a decrease in the thermalization time by more than an order of magnitude, to 0.7 ns.
Data on the evolution of the density of charged particles during plasma decay in dry air (Fig. 16a) indicate that, although, at the beginning of this stage, only simple \({\text{N}}_{2}^{ + }\) and \({\text{O}}_{2}^{ + }\) ions are present, plasma decay occurs when cluster ions \({\text{N}}_{4}^{ + }\) and \({\text{O}}_{4}^{ + }\) are dominant. It is with them that the recombination of electrons occurs in the afterglow of a high-voltage discharge in dry atmospheric-pressure air. In this case, primary molecular ions turn into cluster ions in the processes
and the loss of electrons with a decrease in their density by two orders of magnitude occurs during dissociative electron–ion recombination
The loss of charged particles is also significantly contributed by the processes of three-body electron–ion recombination
When the electron density drops to 1013 cm−3, the three-body electron attachment to O2 molecules,
where M = О2, becomes important. At the later stages of decay, the kinetics of negative ion loss due to ion–ion recombination is turned on. If, at the discharge stage, a large number of atoms and excited particles are produced, collisions with them make possible the detachment of electrons from negative ions, which significantly slows down the plasma decay [98–100].
The presence of Н2О molecules in humid air leads to a change in the composition of positive ions in the discharge afterglow: cluster (hydrated) Н3О+(Н2О)k ions become dominant (Fig. 16b) and the rate of dissociative recombination of which rapidly increases with k and becomes noticeably higher than for cluster ions \({\text{N}}_{4}^{ + }\) and \({\text{O}}_{4}^{ + }\). Therefore, an increase in air humidity leads to an acceleration of plasma decay. This is also facilitated by the efficient attachment of electrons in process (10) for M = Н2О.
The dissociation energy of cluster ions and the binding energy of electrons in negative ions (the affinity of neutral particles to an electron) are small (~1 eV and less) compared to the ionization potentials of neutral particles. Therefore, with the development of a discharge in heated air or with significant heating of it at the discharge stage, the formation of cluster ions sharply slows down and their dissociation and the detachment of electrons from negative ions are accelerated. This effect for pulsed nanosecond discharges in air has been studied best for a streamer discharge in long gaps (see [120–123] and references therein). The effects in heated air for a streamer plasma and its decay have received both experimental and numerical confirmation based on the available kinetic models for positive and negative ions.
In nanosecond discharges with a high (~1 eV per molecule) specific energy deposition, the degree of dissociation of O2 molecules in air turns out to be more than 10% and can reach 80%. This occurs in nanosecond pulsed [124, 125] and repetitively pulsed (repetition rate 10–30 kHz) spark discharges [70, 72] in short (1–7 mm) discharge gaps, as well as in a capillary discharge [126]. The presence of a large number of O atoms in the gas can significantly slow down the plasma decay in the afterglow of such discharges due to the destruction of positive cluster ions and detachment of electrons from negative ions in collisions with atoms. For example, Fig. 17 shows the results of a numerical 1D simulation [127] of plasma decay under the conditions of the experiment [128], in which the decay of a nanosecond spark plasma was studied. Here, near the discharge axis, the loss of charged particles was determined by electron–ion recombination, while the loss of electrons due to their attachment to O2 molecules was compensated by fast electron detachment in collisions between negative ions and O atoms. Only far from the axis, where there are few O atoms, the concentration of negative ions showed noticeably increase. As a result, the radial profile for these ions turned out to be nonmonotonic.
6 FAST HEATING OF AIR IN A STRONG ELECTRIC FIELD
In a weakly ionized gas-discharge plasma, the energy from the electric field is transferred to the main carriers of the electric current, electrons. Further, this energy in collisions with neutrals, mostly inelastic, is redistributed over various degrees of freedom of these particles. Most of the energy is eventually converted to heat. But the gas heating rate strongly depends on the degrees of freedom through which this transition occurs. For example, the relaxation of the energy deposited in the vibrations of molecules proceeds in atmospheric-pressure air at times of the millisecond range and more. For plasma-assisted flow control, of greatest interest is the much faster heating of gas: on a nanosecond time scale. This type of heating, which is called fast heating according to the terminology established in the literature [129–136], as applied to air plasma will be considered below.
The distribution of energy over various degrees of freedom of molecules and the mechanisms of fast heating in a discharge air plasma depend on the reduced electric field E/n. At E/n < 20 Td, fast heating is determined by elastic collisions of electrons with molecules and the excitation of their rotational states, followed by rapid (over several collisions) RT relaxation. At higher values of E/n, this mechanism contributes to fast heating no more than 3% of the total energy deposition. Even the first experiments showed that the fraction of energy that quickly transforms into heat in air plasma increases with E/n and reaches 10–15% at E/n on the order of 100 Td (see references in [135, 136]).
Of greatest interest for plasma aerodynamics is fast heating in higher fields, up to 1000 Td. A quantitative study of fast heating in nanosecond high-voltage discharges in air at a high (~1 atm) pressure is a difficult task, since the plasma in this case is usually highly inhomogeneous.
In experiments [137–139], fast (at times less than 1 μs) heating of air upon initiation of a nanosecond gliding surface discharge was investigated. Based on the processing of the measurement results, it was concluded that the fraction of the discharge energy that quickly turns into heat increases with an increase in pressure from 25 to 230 Torr from about 15 to 60%. The electric field in the discharge was not measured, which does not make it possible to determine the channels through which fast heating in these experiments occurred. The estimated values of the reduced electric field were in the range 100–1000 Td [139].
More consistent approaches to the simultaneous measurement of the fraction of the energy rapidly transferred to heat and the electric field at high E/n were used in [140, 141]. In these works, first, the fast heating of air was investigated by measuring the velocity of the shock wave during its propagation in the plasma of a high-voltage pulsed nanosecond discharge at a pressure of p = 20 Torr, when the discharge was homogeneous. From the processing of the results, it was concluded that the fraction of energy rapidly transferred to heat is 36–40% at times of the order of τ = 50 μs, which corresponds to the product pτ ~ 1 atm μs. According to estimates, the energy deposition in the discharge was carried out at E/n ~ 600 Td. Second, using emission spectroscopy, the fast heating in a pulsed nanosecond SDBD at p = 1 atm was studied, which, in this case, created an inhomogeneous plasma. Measurements were made both during the nanosecond discharge and 1 μs after its termination, for which an additional weak diagnostic voltage pulse was applied to the electrodes, which initiated the glow from the plasma, but almost did not lead to additional heating of the gas. From the processing of the results obtained, it followed that, during the discharge, the fraction of energy rapidly transferred to heat was 30–40% and, 1 μs after the discharge, it reached 55–65%. In this case, the reduced electric field, estimated from measurements by emission spectroscopy, was 800–900 Td. The results of measurements [141] in an SDBD for atmospheric-pressure air were generalized in [142] for the pressure range 300–750 Torr and for other N2 : O2 mixtures. The fraction of energy rapidly transferred to heat remained constant within the measurement error as the air pressure decreased to 300 Torr and significantly decreased with decreasing oxygen content in the N2 : O2 mixtures.
A high-voltage pulsed nanosecond discharge homogeneously developing in the form of a fast ionization wave in air at a reduced (2–7 Torr) pressure was also used in [143] to study the efficiency of fast heating in its afterglow. In this case, the gas temperature was measured by the radiation of the second positive nitrogen system. From the processing of the results, it was concluded that, at times of 50–100 μs (рτ = 0.15–0.9 atm μs), approximately 24% of the energy deposited in the discharge is transferred to heat. The main energy deposition in the discharge occurred here at E/n = 200–400 Td.
Fast heating of atmospheric-pressure air at a gas temperature T = 1000–1500 K was experimentally studied in a repetitive nanosecond pulsed discharge in a short (4 mm) discharge gap between two sharp electrodes [72]. The electric field in the gap during the main energy deposition varied in the range 200–300 Td. The dynamics of the gas temperature was monitored by emission spectroscopy using the second and first positive nitrogen systems. An analysis of the data obtained showed that the fraction of the energy deposited in the discharge, converted into heat in 20 ns, was 21%.
A similar experimental setup was used in [73] to study fast heating in air using schlieren photography, which shows the development of radial inhomogeneities in the discharge gap in a repetitive nanosecond discharge and a diverging cylindrical shock wave generated by it. From a comparison of the results of one-dimensional modeling of gas-dynamic effects and schlieren photographs, the fraction of energy rapidly transferred to heat was determined; 50 ns after the discharge, it was 25% at E/n = 164 Td and increased to 75% at 270 Td. In this case, the initial pressure was atmospheric and the initial gas temperature was in the range 300–1000 K.
Thus, numerous experiments indicate that the efficiency of fast (at times smaller than 1 μs at 1 atm) heating of air in a discharge plasma increases with an increase in the reduced electric field E/n and gas pressure. At high (> 400 Td) electric fields, the energy rapidly transferred to heat in an air plasma becomes of the same order of magnitude as the energy deposited in the discharge.
Kinetic models describing fast heating in air at high values of E/n typical of SDBD are considered in [141, 144]. Both these models are an extrapolation of the model [136], proposed for moderate reduced electric fields, to the region of high E/n. In [136] (see also [145]), the fast heating of the gas for E/n in the range 80–200 Td was explained mainly by the release of excess energy during the dissociation of O2 by electron impact:
upon quenching of electronically excited N2 molecules in collisions with O2:
and when quenching the state О(1D):
For plasma aerodynamics problems, the most interesting is fast heating in fields typical of an SDBD, where they reach 1000 Td. At such electric fields, the excitation of higher electronic states of molecules and their ionization by electron impact become important [136, 141, 144]. Here, energy quickly turns into heat upon the quenching of these states:
upon the dissociation of nitrogen molecules through these states:
and in recombination of charged particles with each other. The spectrum of positive ions in dry air is rather complex, and it changes during the decay of the plasma of a nanosecond discharge (see Section 5). The dominant particles here are the \({\text{O}}_{2}^{ + }\), \({\text{N}}_{2}^{ + }\), \({\text{O}}_{4}^{ + }\), and \({\text{N}}_{4}^{ + }\) ions, and the main process of the recombination of electrons with ions is dissociative recombination:
In humid air, the composition of ions becomes more complicated due to their hydration. In the later stages of plasma decay in atmospheric-pressure air, electrons are lost as a result of the attachment of electrons to the O2 molecules. This is usually three-body attachment with the formation of \({\text{O}}_{2}^{ - }\) ions:
Subsequently, negative ions recombine with positive ones in the processes
with a large release of energy, which can be converted into heat and partly be transferred to the internal degrees of freedom of molecules or spent on their dissociation. The energy released during the recombination of charged particles largely depends on the products of this process.
Models [141, 144] and the simulation of fast heating in air at high E/n, based on them, differ mainly in what the final products are taken in reactions (18), (19), and (21), as well as in the state of the products for some quenching processes of electronically excited molecules. In [141], an approach was used in which, in the absence of reliable information on the reaction products, it was assumed that all the energy released in this case is converted into heat, and the excitation and dissociation of the products were neglected. In this case, the model [141] made it possible to obtain an upper estimate of the efficiency of fast heating of air, which is confirmed by the existing experimental data obtained at high reduced fields and pressures [141, 142]. In [144] under similar conditions an approach was used in which the degree of excitation and dissociation of these products was determined from additional, sometimes not clearly justified, considerations. This reduced the efficiency of fast heating of air due to the formation of excited particles and dissociation of molecules in the products of recombination of charged particles and some processes of quenching of electronically excited molecules. However, a number of assumptions used in this case require additional validation.
Figure 18 shows the calculated [141] fraction of the energy deposited in the discharge that is rapidly transferred to heat in an air plasma as a function of the reduced electric field. For comparison, the figure presents the available experimental data and the results of the calculation of this quantity in [145] and, by a simple approximation formula, which was suggested in [144]. According to this formula, the fraction of energy rapidly transferred to heat in air is equal to 30% of the fraction of the electron energy spent on the excitation of electronic states and dissociation and ionization of molecules. Good agreement is observed between all calculations at not too large (<400 Td) E/n. At higher fields, the results of calculations [141] at 1 atm turn out to be noticeably higher than other calculations presented in Fig. 18. The model [144] has been used many times to calculate fast heating in nanosecond discharges in air under various experimental conditions [127, 143, 144]. In this case, the calculations and experiment showed good agreement in the air heating dynamics. However, under these conditions, the main energy deposition always occurred at E/n < 400 Td, when, according to Fig. 19, different models give close results.
(1) Calculated fraction of energy rapidly transferred to heat in air vs. the reduced electric field [141]. The calculations were performed at different pressures for the electron density neff = 1014 cm–3. For comparison, the results of calculations in (2) [145] and (3) by the approximation formula proposed in [144] are given. Experimental data from (squares) [141], (circles) [143], (triangles) [72], and (inverted triangles) [73] are also given.
Spatial distribution of the fractions of fast heating through the main five channels (in relation to fast heating in all channels) for negative (left, V = –24 kV) and positive (right, V = +24 kV) discharges [146]. The last figure in each group shows the distribution of the specific energy deposition (J/m3).
Experimental data on the fast air heating at higher E/n were obtained only in [141, 142]. Comparison of the results of this experiment and the calculation according to the model proposed in this work for the time evolution of the fraction of the discharge energy rapidly transforming into heat shows reasonable agreement at different pressures, taking into account the fact that the plasma at 1 atm is strongly inhomogeneous and the computational model is zero-dimensional and gives only an upper estimate, since it does not take into account possible excitation and dissociation of products for a number of processes. Note that the fast heating model proposed in [144] cannot describe the only experimental data currently available in the range of high reduced fields and pressures [141, 142], which, apparently, indicates the low reliability of the model [144] under these conditions.
Above, we considered a discharge in air, the composition of which was simulated by an N2 : O2 mixture in the case of dry air and an N2 : O2 : H2O mixture in the case of humid air. The situation changes greatly in discharges with a high specific energy deposition, when the degree of dissociation of the O2 molecules is higher than 10%. Such conditions are realized in nanosecond pulsed [124, 125] and repetitively pulsed periodic (repetition rate 10–30 kHz) spark discharges [70, 72] in short (1–7 mm) discharge gaps, as well as in a capillary discharge [126], where also the fast heating of cold or pre-heated air was investigated. In this case, the typical reduced electric fields were in the range 150–400 Td, the specific energy deposition was ~1 eV per molecule, and the degree of dissociation of O2 was in the range 10–80%. In this case, O atoms became one of the main components of the gas mixture (N2 : O2 : O for dry air). Simulation [127] for these conditions of fast air heating at various (300–1500 K) initial gas temperatures showed that a significant contribution to the fast heating under the conditions considered is made by the processes of quenching of excited N2 molecules on O atoms:
as well as
and
It is important that here the fraction of NO molecules was also high, which affected the fast heating, the production of other nitrogen oxides, and the vibrational excitation of the molecules.
Since, in real discharges, the reduced electric field E/n is highly nonuniform and nonstationary, it is of particular interest to numerically simulate the kinetics of gas heating, taking into account the change in this parameter, when both the electric field and the gas number density vary simultaneously (due to gasdynamic effects). Such calculations were performed in [146] for an SDBD in atmospheric-pressure air, where the 2D model previously developed in [62] was used and the fast heating of the gas was considered within the model [144]. Figure 19 shows the spatial distributions of contributions to fast heating in an SDBD plasma obtained in [146] for five main channels. Calculations were made for a voltage of 24 kV with both positive and negative polarity. It also shows the spatial distributions of the specific energy deposition in the discharge. For both polarities, the main channels of fast heating were the quenching of triplet states N2(C, B) on O2 molecules (Fig. 20) and the specific energy deposition was maximum near the high-voltage electrode and decreased with distance from it. The positive-discharge plasma propagated further, and the gas was rapidly heated in it at large distances from the high-voltage electrode. This distribution of the energy deposition is in qualitative agreement with the experimental data [53], where the dynamics of the development of a nanosecond SDBD in the range 12–760 Torr was studied for a voltage at the high-voltage electrode of ±10 and ±20 kV.
Fractions of fast heating through the main five channels (in relation to fast heating in all channels) and specific energy input for negative (V = –24 kV) and positive (V = +24 kV) discharges vs. the distance from the high-voltage electrode [146]. The data corresponds to a height of 25 μm above the dielectric surface.
Thus, the available experimental studies indicate a high efficiency of fast heating in a discharge air plasma at high (up to ~1000 Td) electric fields and pressures. The main mechanisms providing fast heating of air under the conditions under consideration are generally understood, which permits detailed modeling of the processes allowing plasma-assisted gas flow control.
7 CONTROL OF SHOCK WAVE CONFIGURATION AND LOAD DISTRIBUTION
7.1 The Main Mechanisms of Controlling the Flow around a Supersonic Object
The concepts of methods for reducing aerodynamic drag and heat transfer by means of energy release ahead of the bow shock wave on axisymmetric blunt bodies moving in the atmosphere at supersonic velocities have been discussed and studied for a long time [147, 148]. There are two approaches to explaining the nature of the interaction of supersonic flows with plasma. The first approach describes a process based on a thermal mechanism and is associated with the release of energy in a discharge. In the second mechanism, it is assumed that the plasma effect is mainly caused by the transfer of momentum from charged particles accelerated by the electric field to the neutral component of the gaseous medium. In this case, an important role is played by the uncompensated space charge, which leads to the appearance of a volume force.
In the aforementioned work [7], it was shown that, during the propagation of a shock wave in a discharge tube, the velocity of the wave increases and the amplitude decreases. The authors compared the obtained increase in the velocity with the calculated values corresponding to the heat release of the discharge. The resulting difference (1200–1300 m/s instead of 900 m/s) was explained by additional heating due to relaxation of vibrational energy and quenching of electronically excited states of neutral particles, as well as by the formation of a double layer ahead of the shock wave. However, in later works, this interpretation was called into question [149, 150]. Heating in the discharge was considered as the main cause of the effect of plasma on the gas flow.
In [149, 150], the effect of a nonequilibrium plasma on a shock wave generated ahead of a cone in a supersonic flow at Mach number M = 2.5 was discussed. The experiments were conducted in a wind tunnel using a supersonic plasma flow around a quasi-two-dimensional wedge (Fig. 21). It followed from observations that an oblique shock wave can be significantly weakened when exposed to a plasma of a transverse high-frequency discharge. The resulting attenuation of the shock wave was found to correspond to an increase in temperature in the boundary layers due to gas heating in the discharge.
(a) Schematic of the working section of an RF discharge in a supersonic flow: side view and top view; photographs of a supersonic flow around a cone visualized with a plasma generated by an RF discharge and a DC discharge in a 30% N2–70% Не mixture flow at P0 = 250 Torr: (b) only a 175 W direct current discharge is turned on and (c) with an RF discharge with a power of 250 W added [149].
In [150, 151], the propagation of shock waves from a spark in a glow discharge plasma in argon and argon-nitrogen mixtures was studied. Direct evidence was obtained for the thermal mechanism of the interaction of a shock wave with a plasma of pulsed discharges. With a submillisecond delay between the onset of the discharge and the launch of the shock wave, the plasma parameters reached steady-state values, but the temperature rise remained small for several milliseconds due to the low discharge power. It was shown that schlieren signals turned out to be almost identical to those observed without a discharge, differing significantly from signals in discharges with fully established temperature profiles (Fig. 22). Nevertheless, an important question remains about the possible features of the discharge and the properties of plasma in molecular gases. Significant excitation of the internal degrees of freedom of molecular gases, attachment of electrons to molecules, and lower electron temperatures (strong effect of the double layer at low ionic Mach numbers) can lead to a significant effect of nonequilibrium excitation on the interaction of the discharge with the gas flow. These issues were discussed in [140, 152–154].
(a) Schematic of an experimental setup for studying the propagation of a shock wave in glow discharges; schlieren signals and shock wave velocity in a glow discharge in Ar + 11% N2 at 50 Torr: (b) no discharge, DC discharge at 80 mA, weak (~1 mA) initiating discharge, and pulsed discharge; (c) evolution of the shock wave velocity and the schlieren signal width at a fixed point inside the discharge with a time delay between the onset of the discharge and the launch of the shock wave [151].
In [152–154], the results of studying the structure of strong shock waves in plasma with high reduced electric fields (E/n ~ 10 kTd) are described. The authors obtained the profiles of the rotational gas temperature, the distribution of the electron density and the electric field in the air flow at M = 8.2. Comparison of the experimental and numerical results showed that the change in drag can be fully explained by gas heating during thermalization of a gas-discharge plasma (Fig. 23).
(a) Organization of hypersonic plasma flow and (b) comparison of experimental and numerical results for the change in stagnation pressure vs. the discharge power in an air flow at М = 8.2 [154].
Figure 24 shows the calculated changes in the flow field for various values of the energy deposition in the discharge. The main energy release occurs behind the shock front due to a higher gas density and, as a consequence, a higher energy deposition and specific heat in the processes of electron–ion recombination.
Results of calculations of the flow field for different values of energy deposition in the discharge: (a) without discharge; (b) E = 0.044 eV/molecule; (c) E = 0.049 eV/molecule; and (d) E = 0.054 eV/molecule. Air, М = 8.2, stagnation temperature Т0 = 300 K, static flow temperature T1 = 21 K, and static pressure Р1 = 5 × 10–3 Torr [154]. Dimensions are in [m].
A similar discharge configuration, but at low E/n, was investigated in [155] in a flow at M = 3. It was found that a discharge developing at relatively low values of the reduced field deposits energy mainly in the vibrational degrees of freedom of the gas rather than heat. Numerical simulations have shown the critical role of fast energy thermalization for efficient control of the shock wave configuration and drag. Thus, these regimes are fundamentally different from those studied in [154], where, due to the high values of E/n (~10 kTd), the main direction of energy deposition was gas ionization with fast recombination and subsequent heating.
In [140], studies of the propagation of a shock wave through a decaying air plasma after a pulsed nanosecond discharge (E/n ~ 600–800 Td) are presented. It was found that the velocity of the shock wave increases with an increase in the delay between switching off the discharge and the arrival of the shock wave to the plasma region. This observation made it possible to confirm the thermal character of the interaction of the shock wave with the plasma and to estimate the energy thermalization time in the plasma (Fig. 25).
(a) Experimental scheme for observing the interaction of a shock wave with a plasma of a high-voltage nanosecond discharge and (b) relative change in the shock wave velocity in the plasma region vs. the plasma relaxation time [140].
Figure 26 shows the result of the interaction between a nanosecond SDBD discharge and a bow shock wave in front of the cylinder in the flow at M = 5 [156, 157]. The gas temperature in the plasma layer was only a few tens of degrees higher than the flow stagnation temperature (T = 340 ± 30 K). The interaction of the compression wave created by the expanding gas from the discharge region and the bow shock wave causes its displacement upstream, thereby increasing the distance of the wave departure from the body surface to 25%.
Interaction of the separated shock wave with a perturbation created by a surface discharge. (a) Difference between the schlieren and original signals. Dry air, P0 = 370 Torr. (b) Percent increase in the distance of the shock wave departure after the first and second discharge pulses [156].
Thus, the results of works [140, 149, 150, 152–154, 156] clearly demonstrate the thermal character of the interaction of the shock wave with a nonequilibrium plasma. The theory of interaction of shock waves with hot layers (in fact, with entropy layers of any nature) has been developed many years ago. It has been established that the propagation of the perturbation in the hot layer occurs at a higher speed than in the main flow, which leads to the formation of a so-called precursor ahead of the main shock wave front.
In the works of Nemchinov’s group (e.g., [158]) it was shown that the length of such a precursor at a sufficient overheating of the layer linearly depends on the travel length of the shock wave along the hot layer: l ≈ Us t, where t is the time of interaction of the wave with the heated layer and Us is the velocity of the wave. This relationship was verified up to Us t = (80–90)h (h is the layer thickness) for flat heated layers (two-dimensional flows) and up to Us t = (300–400)d (d is the layer diameter) for heated channels (axially symmetric case). This means that there must be a mechanism that ensures the accumulation of gas in the precursor zone both from the hot layer and from the undisturbed flow region. One of the possible variants of this situation is the separation of the hot layer from the axis or plane of symmetry and the formation of a vortex structure.
In [158], it was found that, up to the ratio of the gas temperature in the heated layer to the temperature of the main flow T '/T ≅ 2.5, the ratio of the precursor length to the shock wave path in the hot layer is in the range ξ = 0.02–0.05 (М = 3, γ = 1.4). Only starting with overheating T '/T > 2.5 the dependence of the coefficient ξ on the value of overheating T '/T was observed. In this case, the value ξ = 0.29 was achieved at T '/T > 5.5.
A criterion of flow restructuring was proposed in [159] and [160] immediately after the first tests of nuclear bombs, in which radiation from the epicenter of the explosion led to the formation of hot layers over the Earth’s surface and intense interaction of the blast wave with these layers. The Mark–Griffiths criterion was based on a comparison of the stagnation pressure of the gas from the entropy layer and the static pressure of the gas in the main flow. It was assumed that the shock wave velocities in the entropy layer and outside are equal at least until the moment when the critical conditions are fulfilled. It can be shown that the condition of invariability of the shock front velocity in all regions de facto prohibits the restructuring of the flow even when the Mark–Griffiths criterion is satisfied. This indicates the inconsistency of the model. Indeed, an estimate based on the Mark–Griffiths criterion at M = 3 and γ = 1.4 indicates the onset of flow restructuring at T '/T > 1.18, which is significantly different from the observed values T '/T (crit) ≅ 2.5.
A modification of the Mark–Griffiths criterion was proposed in [161, 162]. The following requirements were proposed as conditions for the restructuring of the flow from the initial stable propagation of the shock wave to the self-similar growth of the precursor:
(a) the static pressure behind the shock front in the entropy layer must be equal to the static pressure behind the shock wave in the main flow;
(b) the gas velocity behind the shock front in the entropy layer should be equal to the velocity of the main shock wave.
Conditions (a) and (b) mean complete deceleration of the gas from the entropy layer with respect to the front of the main shock wave. Mathematical details can be found in [161, 162]. Below we present the final expression for the critical overheating of the longitudinal thermal layer, at which the self-similar growth of the precursor ahead of the shock wave is initiated:
This criterion quantitatively reproduces the existing experimental results on the interaction of a shock wave with the hot layer and makes it possible to determine the energy required to control the configuration of shock waves in supersonic flows by means of heated layers (Fig. 27) [163].
Another important issue is the minimum possible thickness of the entropy layer at which a stable interaction of the shock wave with the layer is achieved. Minimizing the layer thickness means minimizing the energy consumption and is extremely important in terms of practical flow control. According to the results of [158], a self-similar solution exists at least up to the wave travel lengths along the layer, dx = (300–400)d, with an increase in the precursor length according to a linear law l ~ dx.
These relationships show that one can expect a change in the shock wave shape even when using an entropy layer with a transverse size of about 1% of the object’s size. Figure 28 [164] gives an example of the interaction of an entropy layer of various sizes with a bow shock wave. With a relative layer thickness of 10 and 100% and with the excitation of the entire flow, the decrease in the stagnation pressure relative to the unexcited flow was 21, 34, and 29%, respectively. It is clear that reducing the size of the entropy layer can significantly increase the efficiency of flow control by means of such a layer.
Numerical simulation of the interaction of a shock wave with a heated layer of different thicknesses for air at M = 8.2, T0 = 300 K, and P0 = 35 Torr. Excitation energy E = 0.054 eV/mol, layer thickness: (a) 0; (b) 10; (c) 100%; and (d) the entire flow [164]. Dimensions are in [m].
The approximately equal effects of thin and thick entropy layers on the configuration of shock waves makes it possible to use focused relatively weak excitation of the gas ahead of the shock front. That is why many experiments on plasma-assisted drag reduction were carried out with the generation of thin plasma filaments [165]. Among them are the release of the energy of a pulsed laser [166], the generation of filaments by means of microwave radiation [167], and the injection of opposing jets [168].
In [168], the possibility of controlling the shock wave structure and reducing the drag by gas heating with introducing a hot plasma jet into the main flow was shown. The drag measurements were carried out with injection of both gas and plasma jets. The experiments were conducted at a Mach number of 6. Using a plasma torch, a counter-flow was introduced into the main flow at a Mach number of 3.28. Injection of a plasma jet from a spherically blunt cylinder made it possible to significantly reduce the drag. The schlieren photograph and the calculated pattern in the configuration with a counterflow are shown in Fig. 29.
(a) Schlieren image in an experiment with a counterflow and (b) calculated flow pattern in the case of a counterjet [168].
It may be concluded that the main mechanism of the action of plasma on supersonic flows is heating. The role of the ionic wind under such conditions is, as a rule, negligible and can be excluded from the analysis.
Experiments demonstrate high efficiency in creating small regions of heated gas and controlling the configuration of shock waves and flow. Plasma effects such as space charges and double layer formation should not significantly affect the propagation of strong shock waves. The main problem of controlling supersonic and hypersonic flows using entropy layers is reduced to the technology of creating hot filaments in front of the bow shock wave or transferring the momentum from the discharge behind the shock wave front upstream. To generate a perturbation ahead of the wave, it is necessary to create a plasma filament with specified properties and location in the region of rarefied gas ahead of the wave front.
This problem was clearly demonstrated in [169], where the effect of the energy deposition by means of an arc discharge on the flow with M = 5 around models comprising a truncated cone-cylinder with a half angle of 15° was studied. To initiate an arc discharge, the authors had to place a high voltage tungsten electrode in front of the model (Fig. 30). The effect of the arc discharge turned out to be much weaker than the effect of the electrode itself in front of the model. In addition, the system of such electrodes will be demolished by the flow in all practically interesting conditions.
Schlieren image of the flow around a truncated cone-cylinder: (a) without electrode; (b) without discharge, and (c) with discharge [169].
7.2 Generation of Perturbations in Front of a Supersonic Object
Microwave radiation, lasers, and electron beams are currently being considered as methods for creating plasma in front of a body in a flow [150, 151]. In this case, a combination of several methods of plasma generation may be promising; for example, the use of jets or laser and electron beams to localize the deposition of energy of microwave radiation or short high-voltage pulses [170]. Below we will analyze several of the most important works using such methods.
7.3 Microwave Discharge
In [167], the results of controlling the structure of the bow shock wave by formation of a thin plasma layer using a microwave discharge were presented. The plasma filament was formed in 1–2 ns and had a transverse size of not more than 3 × 10–3 cm with a specific energy deposition of about 7 eV per particle with a peak electron density пе ≅ 5 × 1016 cm–3.
Gas heating in the filament was approximately 2800 K at a heating rate of ~2000–3000 K/µs. Time-resolved measurements showed that the discharge significantly changes the configuration of the bow shock wave due to the formation of a hot filament. Figure 31 shows the propagation of a bow shock wave through a heated zone with the formation of the same structures that were observed when the shock wave interacts with typical hot layers (see Fig. 28). The interaction of filaments with the head shock wave after 60 and 85 µs is shown in schlieren photographs (Fig. 31, left). In this case, one can see the formation of vortices, which appear in the figure in the form of light regions in the glow distribution fields (Fig. 31, right).
Interaction of microwave filaments with a flow near a blunt body. (Left) Schlieren images and (right) glow distribution fields 60 and 85 μs after microwave discharge [167].
It was shown in [167] that the energy efficiency of reducing the stagnation pressure is directly proportional to the ratio D/d, where D and d are the diameters of the model and the plasma filament, respectively. This relationship has been proved for model diameters of 8 to 30 mm. These results confirm the conclusion of [158, 161, 162] about an increase in the interaction efficiency (the efficiency in a decrease in aerodynamic drag) with a decrease in the thickness of the heated layer.
A further development of this research are microwave discharges initiated by laser plasma [171]. Relatively weak ionization by laser radiation can initiate the release of microwave energy and cause fast heating of gas. In this case, precise localization of the energy release of the microwave discharge and even the simultaneous creation of several localized plasma regions using the same microwave pulse are possible. The interaction between the plasma produced by the seed laser pulse and the microwave pulse is shown in Fig. 32. An increase in the energy of the femtosecond pulse of the seed laser led to a significant change in the character of the discharge propagation process. With an increase in the pulse energy by a factor of 3, the discharge ignition was observed along the entire length of the Rayleigh region near the focal point of the seed laser beam. In this case, the region of strong coupling between the laser plasma and the microwave pulse energy increased significantly (Fig. 32, [172]).
(a) Evolution of a laser pulse and microwave discharge in air: evolution of an optical discharge without a microwave field and (b) evolution of an optical discharge in a microwave field [172].
7.4 Laser Spark
The first observations of the possibility of flow control using pulsed energy release from a laser-induced optical discharge appeared as early as the 1980s [173]. In [166], the effect of pulsed energy deposition on the flow around a sphere at M = 3–4.5 was studied. In all experiments, the energy deposition was provided by a pulsed Nd:YAG laser (532 nm, pulse duration 10 ns, repetition rate 10 Hz) with energy levels from 12 to 300 mJ. A single laser pulse created a hot spot in front of the spherical bow shock wave. Figure 33 shows the interaction of this spot with the shock wave. The results (Fig. 33b) confirm the conclusion of [158, 161, 162] about the weak dependence of the interaction dynamics on energy if the perturbation intensity is above the interaction threshold.
(a) Interaction of a bow shock wave with a laser-heated spot and (b) time variation of the stagnation pressure on the center line of the body at laser pulse energies of 13, 127, and 258 mJ [166].
In [91], the interaction of a shock wave at M = 3 with a plasma formed by radiation of a femtosecond laser was studied. A femtosecond pulse differs from a nanosecond pulse in a fundamentally dissimilar mechanism of plasma development: in this case, most of the electron–ion pairs are formed not as a result of avalanche ionization by electron impact, but as a result of multiphoton ionization of molecules. In this case, the heating of the gas during the laser pulse is negligible and the main increase in the temperature of the heavy component occurs during the recombination of the forming plasma. It was found that the release of energy during such a decay of the laser plasma in front of the body in a supersonic flow causes a significant, albeit short-term, drag reduction. Figure 34 shows schlieren images of the flow development when the gas is excited ahead of a bow shock wave by means of a terawatt laser pulse with a duration of ~50 fs. The mean wavelength of the laser pulse was 800 nm, and the maximum pulse energy measured at the edge of the test model was 150 mJ/pulse.
Schlieren images of a flow interacting with a decaying laser plasma of a femtosecond laser [91].
In [174], an attempt was made to describe the interaction of a laser plasma with a shock wave from first principles, starting with the formation of a laser spark until the moment when a gasdynamic perturbation develops. Gasdynamic effects were described using the Navier–Stokes equations taking into account nonequilibrium chemical reactions in the two-temperature approximation (for heavy particles and free electrons). The calculations were performed in supersonic and hypersonic air flows for a spherical blunt body and a body in the form of a double cone (Fig. 35). The development of an optical discharge was simulated using the kinetic approach for photons taking into account the process of inverse bremsstrahlung, leading to the heating of electrons, but neglecting the scattering of laser radiation by the forming plasma region, which has a negative refractive index at ω < ωpe, leading to a significant enhancement of the observed effect. The simulation results qualitatively confirm that localized energy release can be effectively used to control shock wave shape.
Isolines of Mach number 2 μs after 600 mJ laser pulse focused 5 mm upstream; (right) enlarged image of the interaction of a laser shock wave and the main conical shock wave with a density gradient and a pressure gradient [174].
Thus, recently, it has been convincingly shown that the main mechanism of interaction of a laser plasma with a flow—regardless of the duration of the laser pulse—is the heating of gas as a result of plasma decay. On the other hand, the drag reduction obtained in such experiments and calculations, as a rule, becomes significant only for blunt bodies. If the object has a high aerodynamic quality, it is usually not possible to obtain a significant reduction in the drag coefficient [175]. However, an off-center action on a fast-moving object can lead to a distortion of the symmetry of the force distribution and significantly change its trajectory.
8 CONTROL OF THE TRAJECTORY OF A SUPERSONIC OBJECT
In paper [176], an experimental and theoretical analysis of the trajectory control of rapidly rotating supersonic objects using a laser spark was reported. To carry out such experiments, a special pneumatic suspension was designed, which ensured the spinning of the model in a supersonic flow and the possibility of changing the axis of rotation of the model without friction. A laser spark was generated by an Nd-YAG laser (radiation wavelength 1.06 μm, pulse energy 300 mJ, pulse duration 5 ns). It was shown that the spark generates a strong shock wave, a spot of hot gas, and a slow air jet at a late stage in the decay of the perturbation, directed towards the radiation source. Gas heating was considered as the main mechanism for pressure redistribution over the surface of an object and changing its position in space. Three series of experiments were carried out.
The first series demonstrated the destabilization of a rotating object by a single laser spark. In the second and third series, the dynamics of the change in the angle of attack of the object by means of 3 consecutive laser sparks following each other with an interval of 50 to 100 μs was analyzed. In all three cases, the possibility of destabilizing the trajectory of a rotating object was demonstrated (Fig. 36, single spark). The duration of the perturbation effect in the position of the object’s axis corresponds to the propagation time of the hot spot along its surface (~50 μs). The low-density gas region causes pressure redistribution and maintains the development of the trajectory perturbation (Fig. 36). After the hot spot formed by the laser spark leaves the interaction region, the perturbation of the object’s axis of rotation decreases. Increasing the number of consecutive pulses prolongates the duration of the unstable motion of the object. Thus, the ability to control the trajectory of a rotating object strongly depends on the duration of interaction, which is limited by the length of the laser spark in the direction of the trajectory of the object.
The theoretical analysis performed in [177] made it possible to extend analytical criterion (25) of strong interaction between the shock wave and the hot layer to the case of an arbitrary angle of inclination of the shock wave, α:
It was shown that the critical temperature of the hot layer increases with a decrease in the angle of inclination of the wave relative to the direction of the flow and decreases with an increase in the Mach number of the shock wave (Fig. 37).
Critical temperature in the hot layer vs. the Mach number, depending on the angle of inclination of the shock wave relative to the flow direction [177].
Thus, for a plane shock wave (α = 90°) at M = 3, the dimensionless critical temperature of the hot layer is T '/T = 1.8. For an oblique shock wave (α = 40°), the strong interaction regime requires T '/T = 6.5. Numerical modeling shows good agreement with the theoretical predictions.
Based on the experimental and theoretical data obtained, it was concluded that the trajectory control of rotating objects by laser discharges is highly efficient. The energy required to deflect the trajectory of the object by Δα = 1° is determined by the efficiency of the gas layer heating in front of the object, the length of interaction, and the critical diameter of the emerging hot spot. Estimates show that the minimum energy of the laser spark required to change the direction of the trajectory of a standard 7.62-mm bullet by Δα = 1° for an interaction length of ~3.5 cm is about 2 mJ.
In [176], this study was extended to objects with a caliber of 30 mm in a flow at M = 4. A long laser spark in front of the object was generated using an Nd-YAG laser with a pulse energy of E = 2.84 J at a wavelength of 1064 nm. It was shown that the side force created is sufficient to deflect the trajectory of such a heavy object by more than 10 meters at a distance of 1 km. Later, similar experiments were conducted in [178]. The experiments were carried out in a supersonic wind tunnel at Rutgers University to quantify the effect of the release of laser spark energy on the flow field around a pointed cylinder at a free flow Mach number of 3.4.
In [179], the effect of an off-axis optical discharge on the flight dynamics of a body at М = 3.4 was studied numerically. Data on the drag reduction, lateral force, and moments were obtained, and the structure and dynamics of the flow were considered. It was shown that an excessive increase in the radial distance of the discharge from the axis of the object reduces the effect. An assumption was made that there is an optimal distance of the optical discharge from the object’s axis, which gives the maximum lateral force for a given specific absorbed energy.
9 CONTROL OF QUASI-STATIONARY SEPARATED FLOWS AND LAYERS
9.1 Control of Mixing Layers and High-Speed Jet Noise
The control of high-speed mixing layers by means of pulsed energy release in a localized nanosecond spark discharge (LAFPA) was proposed in 2009 in [180]. A system of eight synchronized spark actuators located along the perimeter of a circular submerged jet created local perturbations in the mixing layer. In this case, various combinations of the phase shift of the ignition of individual dischargers made it possible to excite various modes of instability in the mixing layer to control the mixing rate and the noise of the submerged jet. It was shown in [181] that the jet responds to control by means of such a pulsed energy release in a wide range of Strouhal numbers and azimuthal modes (Fig. 38) when operating in a wide range of Mach numbers (from 0.9 to 1.65) and Reynolds numbers (from 0.2 × 106 to 1.65 × 106). The effect of such synchronized spark discharges on jet mixing was studied numerically in [182]. It was shown that the asymmetric action of the actuators destroys the symmetry of the vortices in the layer, significantly enhancing the mixing.
Effect of variations in the Strouhal number in the frequency of operation of nanosecond spark discharges on the flow structure: M = 1.3 [180].
The effect of plasma ns-SDBD actuators on turbulent shear layers (both in the case of a conventional mixing layer and a flow near a wall with a backward step) was experimentally studied in the series of works [183–187]. The objective of these works was to give an idea of the fundamental processes in the control of the mixing layer of a submerged jet by means of thermal perturbations. From the results obtained, it follows that thermal perturbations cause local large-amplitude perturbations of the flow, the effect of which strongly depends on the ratio between the spatial scale of thermal perturbations and the thickness of the mixing layer. This result fully confirms the conclusions of works on the control of boundary layer separation by means of pulsed energy release in an ns-SDBD [33], in which a strong dependence of the actuators’ efficiency on the Reynolds number of the flow was found.
9.2 Controlling the Interaction of a Shock Wave with a Boundary Layer
Controlling Shock Wave–Boundary Layer Interaction (SWBLI) by means of plasma actuators is an important problem of supersonic internal aerodynamics and has been studied for a long time [188, 189]. In these works, a direct current discharge in a magnetic field of 1–5 T caused both heating of the gas in the boundary layer and an acceleration or deceleration of the flow, depending on the direction of the Ampere force. It was shown that the discharge can initiate separation of the boundary layer, enhance, or weaken it. An increase in the gas temperature as a result of energy release in the discharge enhances the separation of the boundary layer, while the acceleration of the gas by magnetogasdynamic forces reduces the size of the separation “bubble” and moves it downstream.
Thus, the control of the shock wave–boundary layer interaction by means of only pulsed heating leads to a contradiction. An increase in the gas temperature in the boundary layer easily leads to an enhancement of this interaction and an increase in the size of the separation zone. As a rule, this effect is undesirable, because the separation bubble can block the flow in the supersonic air intake. To resolve this contradiction, it was proposed in [190] to use localized pulsed spark discharges to create local perturbations in the boundary layer, leading to the formation of large vortices and the introduction of an additional momentum from the main flow into the boundary layer. However, in subsequent works (see, e.g., [191]), it was found that such localized spark discharges displace the reflected shock wave upstream by about the boundary-layer thickness. Based on the results of Particle Image Velocimetry (PIV) measurements with phase synchronization, as well as parametric studies, it was concluded that the effect of spark discharges on the flow reduced to the boundary layer heating above the point of interaction with the shock wave, which is known to be undesirable effect.
A solution was proposed in [29], where, for the activation of the boundary layer, instead of high-temperature spark discharges, surface dielectric discharges with a limited energy deposition were used. In this case, the heating of the gas in the boundary layer decreased by a factor of several tens and the gasdynamic perturbations introduced by the discharge into the flow remained sufficiently intense.
In [192, 193], a detailed study of the mechanism of controlling the shock wave–boundary layer interaction by means of a surface nanosecond barrier discharge was carried out (Fig. 39). Figure 40 shows the dynamics of the propagation of a shock wave arising from the pulsed energy release in the plasma. In 32 μs, the shock wave turns into an acoustic perturbation, and the perturbation from it becomes weak. However, the perturbation of the flow in the boundary layer, caused by the appearance of a slanted bump of low-density gas, provokes mixing of the boundary layer with the main flow, accelerates the gas in the boundary layer, and sharply decreases the height of the separation bubble in the interaction zone (Fig. 40). Such a decrease in the interaction zone indicates that the momentum transfer to the boundary layer as a result of the formation of a vortex on the slanted energy release zone becomes more significant than the effect of gas heating in the boundary layer, which leads to enhancement of the interaction.
(a) Supersonic wind tunnel for SWBLI research and the schematic of the actuator and shock wave generator. (b) Asymmetrical actuator angled 18° relative to the flow; (top) a closed electrode and (bottom) an open electrode; the flow is directed from left to right [193].
(Left) Propagation of a shock wave created by a pulsed discharge (a) 8, (b) 16, (e) 24, and (f) 32 μs after the pulse. (Right) The motion of the reflected shock wave shows a decrease in the size of the separation zone: (c) 0, (d) 16, (g) 224, and (h) 520 μs after the pulse [193].
Figure 41 shows that, with an increase in the high-voltage pulse repetition rate, the effect of heating becomes stronger. At a repetition rate of 5 kHz, the effects of mixing and heating practically compensated each other and, at higher frequencies, the effect of heating prevailed, which led to an increase in the size of the separation zone [193].
The vertical size of the separation zone at SWBLI vs. the repetition rate of high-voltage pulses [193].
In [194], the development of a perturbation in the boundary layer and the interaction of such a modified layer with a shock wave were simulated numerically. In this case, the data on the energy distribution in the discharge, obtained in [53], were used. Figure 42 shows the result of this numerical analysis. It is seen that the boundary layer becomes much thinner as a result of the perturbation (78th μs); then the region of the thin boundary layer is carried by the flow into the interaction region (98 and 163 μs), which leads to a significant reduction in the size of the separation region (258 μs). Thus, the thermal slanted bump created in the boundary layer leads to a significant restructuring of the flow and the region of interaction with the shock wave.
9.3 Control of the Laminar–Turbulent Transition and Turbulent Boundary Layers
In [195], suppression of Tollmien–Schlichting waves under the action of plasma actuators operating in a pulsed mode was observed. These waves, which are precursors of flow turbulization, were artificially excited in the experiment by a special vibrating plate flush-mounted in the channel wall, and amplified by a specially created pressure gradient in the gas. The plasma actuator was located downstream of the wave excitation region. The action of the actuator gave rise to a nonstationary force in the boundary layer, which caused the damping of the waves. As a result, the amplitude of the velocity oscillation at the excitation frequency decreased significantly. The influence of various parameters of the actuator on wave damping was studied. The studies were conducted in an open-cycle wind tunnel with a cross section of 0.45 × 0.45 m2 and a length of work section of 2 m. The inserts on the lid of the work section created a reverse pressure gradient of 25 Pa/m. The boundary layer thickness was 5 mm at x = 590 mm, resulting in a Reynolds number Re = 1100 [195]. Figure 43a demonstrates the work section design, and Fig. 43b shows specificities of the location of the actuator.
(a) Working section and (b) specificities of the position of the actuator [195].
Figure 44 gives more detailed information on the excited frequencies and the mode of oscillations with and without the plasma actuator. Figures 44a show the power spectra for velocity fluctuations, and Fig. 44b gives time markers for these fluctuations. Under the action of the actuator, the oscillation amplitude at the fundamental frequency noticeably decreases, while the f2 and f3 modes remain unchanged. The f4 mode vanishes against the background noise.
(a) Power spectra of pulsations and (b) oscillograms (thick lines) with and (thin lines) without switching on of the actuator. Point x = 590 mm, y = 1 mm [195].
An interesting result was recently demonstrated in [196]. Plasma actuator assemblies with pulsed power supply, installed on the surface of a flat wall, were used to reduce the frictional drag on the surface in turbulent boundary layers. The assemblies were destined to create a plasma-induced near-wall flow in the direction perpendicular to the main flow in order to prevent the rise of low-velocity near-wall vortices into the main flow [196]. Two different assembly designs were used (Fig. 45). The first (a) creates a unidirectional flow, and the second (b) generates a series of oppositely directed jets. The authors claim that both configurations exhibit unprecedented levels of drag reduction by more than 70%. This statement deserves a very detailed consideration. Let us present the data from [196] on the drag reduction for both types of actuators used (Fig. 46).
Schematics of two assemblies of pulsed plasma actuators used in experiments on the reduction of friction drag [196]. The electrodes are oriented along the main flow (the direction of the velocity vector is through the figure plane), while the induced flow is directed across the main flow: (a) unidirectional flow and (b) oppositely directed jets.
Percent variation in drag relative to the baseline vs. applied voltage and Reynolds number; (left) data for a symmetrical assembly of oppositely directed actuators; (right) data for asymmetric assembly of unidirectional flow actuators, according to [196].
The authors of [196, 197] believe that the drag reduction achieved depends on the number of elementary vortices between adjacent surface electrodes. This drag reduction exponentially increases with decreasing ReΘ (ReΘ is the Reynolds number calculated from the thickness of the momentum displacement in the boundary layer) as a result of a decrease in the number of elementary vortices under simultaneous control. This statement makes it possible to analyze the dependences obtained in [196, 197] in the “drag reduction–ReΘ” coordinates (Fig. 47).
Percent variation in drag relative to the base point vs. the Reynolds number of the flow: (dots) data [196] for symmetric and unidirectional actuators at different electrode voltages.
Figure 47, analogs of which are given in [196] in a somewhat truncated version, shows the problem of these works. On the one hand, the data does show a decreasing exponential relationship between the drag reduction and the Reynolds number of the flow. On the other hand, a small extrapolation of the dependences found in [196, 197] predicts the presence of a region of negative absolute drag force at low Reynolds numbers.
Thus, the data [196, 197] contain some contradiction. We do not undertake to unambiguously determine the nature of this contradiction and can only assume that the perturbations introduced by the actuator in the near-wall region led, under conditions [196], to global separation of the flow. The actuator and the measuring plate fell into the region of reverse flow near the wall, which caused a change in the force measured. It should be noted that there is still no final solution to this problem, and, apparently, further studies are needed to confirm or refute the possibility of such a significant reduction in turbulent drag by means of pulsed near-surface discharges. In particular, the answer to the question about the nature of the phenomenon could be given by synchronous measurements of the drag force not only directly on the plate with actuators, but also on the surrounding wall sections.
10 CONTROL OF BOUNDARY LAYER SEPARATION AT HIGH ANGLES OF ATTACK
10.1 Flow Separation Control Using Ionic Wind
In contrast to the case with strong shock waves, most works devoted to the control of slow subsonic flows note the role of plasma effects (in particular, ionic wind) in the flow acceleration in the boundary layer. This acceleration leads to the generation of high-velocity near-wall gas jets, which suppresses the boundary layer separation and can be used to control the position of the laminar–turbulent transition [2].
A near-surface plasma layer can be created in various ways. For example, in [198, 199] and later publications [200, 201], DC discharges with electrodes located above or on the airfoil surface were used. In this case, the ionic wind generated in the discharge can accelerate the flow in the boundary layer up to 3–5 m/s [174].
In [8–12], another approach for creating a plasma layer near the surface in order to control the flow was proposed. This approach is based on the initiation of a surface DBD discharge by applying an alternating sinusoidal voltage. The discharge developed over the surface in the form of thin streamers above the lower encapsulated electrode [203]. This type of plasma actuator and its modifications are being intensively investigated at present [2]. In [204], the creation of a force at a level of 0.2 mN/W by an asymmetric actuator was demonstrated. Almost the same result (0.3 mN/W) was obtained in [205]. The flow velocity under the action of such actuators can reach 5 m/s [10]. In [202], an induced velocity up to 8 m/s was obtained. This flow acceleration provides effective control of the velocity profile in the boundary layer, as well as its separation at flow velocities of several tens of meters per second.
It seems that physical limitations on the maximal ionic wind velocity in the discharge [206] due to the impossibility of increasing a DC electric field above the gas breakdown threshold and to strong frictional losses in the near-wall layer do not allow significant progress in improving the efficiency of actuators using this flow control mechanism. At the same time, in subsonic aerodynamics, the velocity range from 100 m/s (aircraft take-off and landing speed) to 250 m/s (cruising speed) is very important. Thus, advancing to the region of higher speeds is an important and relevant task.
10.2 Flow Separation Control Using Pulsed Energy Release
In [207], it was proposed to use in a plasma actuator a pulsed nanosecond discharge. The values of Е/п in discharges of this type can exceed several-fold the breakdown threshold. High values of the reduced electric field appear to be an obvious advantage of this discharge. Other advantages of this idea are the relatively low power consumption in the discharge and the possibility of initiating such discharges in a wide range of pressures, flow rates, and gas composition, including those with high humidity. The first experiments [207] showed that, using a nanosecond pulsed discharge, it is possible to reliably control the boundary layer separation at velocities up to 75 m/s and specific power consumption lower than 1 W/cm of the wing span.
Later, the effect of a pulsed sliding discharge on flow separation was experimentally studied in [208]. Here, the high efficiency of the pulsed discharge has been demonstrated up to velocities of 110 m/s. At the same time, it was concluded that the main mechanism of plasma effect is the perturbation introduced into the boundary layer rather than gas acceleration. It was shown that changing the pulse rate in the actuator makes it possible to optimize its effect on the drag, lift, and flow reattachment. The optimal frequency turned out to be fopt ~ U∞/L, where U∞ is the main flow ve-locity and L is the typical distance along the surface to the separation zone. Later, this result was confirmed experimentally [209] for chord Reynolds numbers up to 106 and a maximum free flow velocity of 60 m/s.
The scaling of the effect of a nanosecond pulsed plasma actuator was studied in [210, 211]. Experiments on flow separation control were carried out on a rectangular (dimensions 0.5 × 1 m2) wing using a DBD discharge in a subsonic flow with chord Reynolds numbers Re = (0.35–0.875) × 106. Measurements of surface pressure and flow visualization showed that plasma actuators can significantly reduce or completely eliminate flow separation from the wing, which leads to the recovery of a negative pressure peak near the leading edge on the upper surface of the airfoil (Fig. 48). The data were obtained over a wide range of angles of attack, flow rates, plasma excitation frequencies, and input power. The work also discussed the possibility of using different voltage pulses, including microsecond and nanosecond pulses. As in [208], it was shown that the efficiency of the actuator strongly depends on the discharge frequency (Fig. 49).
Pressure distribution over the airfoil surface [210]; (upper group of curves) data for the upper surface and (lower group of curves) for the lower surface; α = 19°; U∞ = 19 m/s, V = 24 kV; Re = 0.8 × 106; (a) periodic mode and (b) pulse burst mode.
Lift, drag, and their ratio vs. the actuator frequency (α = 22°, U∞ = 17.4 m/s): (a) periodic mode, P = 2.5–250 W at f = 102–104 Hz, respectively, and (b) pulse burst mode at P = 25 W [210].
In [212], flow separation on a rectangular wing using a nanosecond SDBD discharge in the case of a transonic flow at chord Reynolds numbers in the range (0.5–2) × 106 was experimentally studied. The experiment was carried out in a wind tunnel at a transonic velocity. The system was upgraded for experiments in pulsed mode. The nozzle with a working chamber operated at Mach numbers from M = 0.6 to M = 0.9. A photograph of the model and a pressure measurement diagram are shown in Fig. 50. The effect of the discharge on the flow pattern near the surface was investigated. The discharge frequency in the experiments was f = 5 kHz. High-voltage pulses with an amplitude of 25 kV and a duration of 12 ns were used. The energy in one pulse was 10 mJ. The angle of attack varied from 0° to 30°.
Photograph of the model and the scheme of pressure measurement in the wake. The chord of the model is 15 cm, the span along the leading edge is 30 cm. The pressure distribution was measured in the wake of the model and on its surface [212].
At small angles of attack, a flow regime without separation was observed, but a local supersonic zone and a buffet shock wave were formed. These modes were clearly indicated by the pressure jump in the middle of the profile surface. This jump is associated with the position of the buffet shock (Fig. 51). The effect of the discharge at small angles of attack in the range α = 0°–15° was insignificant. At higher angle of attack, flow separation was observed, and the character of the pressure distribution changed (Fig. 51). In this case, switching on the discharge returned the flow to the attached regime with the formation of a buffet shock over the upper surface and the corresponding jump-like pressure change. The plasma actuator also removed high-frequency pressure pulsations in the wake. The data presented in Fig. 51b demonstrate a decrease in the pulsation level at a Mach number М = 0.7. Sensor No. 1 detected the pressure on the upper surface of the model and served as an indicator of changes in the angle of attack. Sensors Nos. 2–4 were located in the wake of the model and detected the vanishing of pressure pulsations after switching on the discharge. This effect was observed at high angles of attack (starting with α = 24°) for Mach numbers М = 0.65–0.75. In this case, the mean pressure near the surface of the model did not change significantly, while the high-frequency pulsations of the pressure amplitude in the wake sharply decreased.
(a) Pressure distribution on the surface of the model with and without discharge, Mach number M = 0.74 and (b) reduction of the noise level in the wake of the model, Mach number М = 0.7. Static pressure is P = 1 atm [212].
Thus, the analysis of flow separation control using an SDBD actuator for the C-141 airfoil at transonic velocities (М = 0.65–0.75) led to the conclusion that flow separation was effectively suppressed at angles of attack from 18° to 30°. The discharge reduced both flow separation and high-frequency pressure pulsations in the wake. These experiments demonstrated the possibility of controlling the separation of a transonic flow by means of low-energy pulsed nanosecond discharges. It is important that a nanosecond pulsed discharge has demonstrated an extremely high efficiency of operation in aerodynamic plasma actuators for a wide range of velocities (М = 0.03–0.75) and Reynolds numbers (Re = 104–2 × 106).
For technological applications, it is important to understand the physics of the operation of nanosecond plasma actuators (see the section “Nanosecond surface barrier discharges”) and the differences of this type of discharge from other SDBD discharges in terms of their efficiency [33, 35, 213–217]. From this point of view, there are several important stages. In [208], it was experimentally shown that a pulsed nanosecond high-voltage discharge, which makes it possible to control the flow separation in a wide range of free-stream flow velocities, does not lead to gas ac-celeration. In [218], the possibility of using an A-C‑SDBD actuator generating a surface jet against the main flow was numerically analyzed. According to calculations, such an actuator caused a transition of the boundary layer to a turbulent regime, creating a more “complete” velocity profile. This feature was used to delay the flow separation on the NACA-0015 airfoil at high angles of attack using a pulse actuator in a counter-flow regime. Thus, it was shown in [218] that the gas acceleration along the flow is not necessary to control the boundary layer. Taking into account that AC-SDBD leads to significant heating of the gas in the boundary layer due to plasma recombination and relaxation of the internal degrees of freedom of the gas, the mechanism of the action of plasma actuators based on slowly varying voltages still needs detailed justification. Probably, it is this not very efficient (in comparison with nanosecond discharges) heating of the gas in the boundary layer that is the determining mechanism of the effect of AC-SDBD actuators on the flow and the slight acceleration of the near-surface layer due to electrostatic effects is an insignificant side effect.
In [213], the mechanism of the effect of a pulsed nanosecond high-voltage discharge on the separation of the boundary layer was experimentally demonstrated. It was shown that fast thermalization of a nonequilibrium plasma (on a time scale of hundreds of nanoseconds) produces a heated high-pressure gas layer in the discharge zone, followed by the formation of a strong shock wave. It was suggested that the propagation of a heated gas region causes strong perturbations of the flow and favors its reattachment due to the formation of large vortices in the shear layer between the free flow and the separation bubble [213]. Later measurements of the flow velocity distribution [219] showed that a nanosecond SDBD plasma acts as a pulsed source of large-amplitude perturbations, which control the flow stability and lead to the formation of coherent vortices at the boundary of the separation zone at supercritical angles of attack. These coherent structures interact with the main flow, leading to the mixing of the gas in the main flow and the separation bubble. Numerical simulations of the development of ns-SDBD also show the rapid formation of a plasma layer, gas heating, and generation of shock waves [32, 220].
In [215], the process of interaction of a nanosecond pulsed discharge plasma layer with the flow and the formation of perturbations and vortices were studied in detail. The experiment used a model of the NACA 63-618 airfoil with a chord of 20 cm and a span of 40 cm. The effect of several different actuators, including single, double and triple ones, was studied. The flow velocity was 30 m/s. Some of the results obtained are shown in Fig. 52. In the figure, we clearly see a shock wave created by the actuators and the structure of large vortices developing 40 μs after the discharge [215]. It was noted that, after 2–3 discharges, the flow pattern completely changed: the flow attached and the separation zone shifted downstream. It turned out that the placement of the second actuator at the point where the flow separated after installing the first actuator led to a further shift of the separation point downstream. With the use of three actuators, this made it possible to achieve flow reattachment along the entire airfoil up to an angle of attack α = 32°. The total power consumption was lower than 1 W (25 mW/cm) for an airfoil with dimensions 40 × 20 cm2 at a flow velocity of 30 m/s.
Dynamics of reattachment of the boundary layer; U∞ = 30 m/s, α = 26°, NACA 63-618 airfoil with a chord of 20 cm and a span of 40 cm; discharge energy of 5 mJ per pulse, discharge frequency of 200 Hz in pulsed and burst modes, 10 pulses in one burst [215].
The typical reaction time of the system was 10–15 ms and was close to the time of vortex propagation along the profile surface, which corresponds to the dimensionless frequency of the excitation force \(F_{c}^{ + }\sim 1\) (Fig. 52). It is seen in the figure how the perturbations generated by the pulse actuator initiate the development of instability in the mixing layer. This instability propagates along the layer; additional mixing brought the additional momentum from the main flow to the separation region and reattaches the flow. It should be noted that the discharge energy plays a secondary role here: two different modes (repetitive pulse mode and a burst mode) shown in the figure in odd and even columns, respectively, demonstrate almost the same dynamics of flow reattachment, although the discharge energy in the second case is 10 times higher. A similar conclusion was made in [221], where the perturbation development dynamics was studied as a function of the energy deposited in the plasma. This effect arises because the flow control utilizes development of an instability, whose final amplitude only slightly depends on the initial perturbation amplitude.
It should be noted that the development of instability in the mixing layer is caused not by a shock wave that appears immediately after plasma thermalization and leaves the interaction region at times shorter than 100 μs (second line in Fig. 52), but much later, when a low-density gas from the discharge region reaches the beginning of the separation zone (1 ms and further, curve 3 in Fig. 52). In [215], this approach was used to simulate the development of instability under the action of a ns-SDBD actuator on the separated flow behind the step. In this case, the classical Kelvin–Helmholtz instability, which develops at the boundary of the main flow and the separated flow due to the velocity gradient in this region, is initiated by a spot of low density gas, entering the velocity gradient region, rather than the initial shock wave. The shock wave does not affect the instability development under these conditions, since the difference in the gas densities in the separation zone and in the main flow at subsonic flow velocities is small, and the Richtmyer–Meshkov instability arising between two contacting continuous media of different densities when the interface experiences an acceleration pulse, caused, e.g., by the shock wave, does not develop. The same conclusion was made recently in [222], where the role of various mechanisms on the perturbation development was analyzed.
In [223], the effect of pulsed optical discharge near the leading edge of an airfoil on the boundary layer separation at zero angle of attack was investigated. A laser spark was generated across the leading edge of the airfoil and the flow, forming a region of highly heated gas immediately in front of the model. It was shown that the shock wave resulting from the expansion of the heated region does not affect the separation bubble. The effect on the separation region was explained by strong turbulence in the low-density gas region created by the laser spark.
In [224], where the effect of ns-SDBD on flow separation was studied, almost identical patterns of the interaction of the perturbation with the separated flow were obtained. The authors of [224] suggested that the interaction of the actuator with the separated flow may be due, in addition to the fast-heating mechanisms (quenching of electronically excited molecules and charged particle recombination [141, 142, 225]), by mechanisms of relatively slow relaxation of vibrational degrees of freedom. It is obvious that the energy deposited in the vibrational degrees of freedom will be thermalized. However, at temperatures close to room temperature, relaxation of the main reservoir of vibrational energy—excited states of molecular nitrogen—is very slow. At typical interaction times (less than 1 ms in Fig. 52), this energy remains frozen in vibrational degrees of freedom and cannot participate in the process. In addition, the typical values of the reduced electric field, which are appeared in ns-SDBD, lead to the predominant energy deposition to the electronic degrees of freedom and ionization, which also strongly limits the role of the vibrational degrees of freedom in this process.
An indirect confirmation of the absence of a noticeable effect of slow heating on the efficiency of the operation of nanosecond actuators is the results of numerical simulation of the effect of such actuators on separated flows [226, 227]. In these works, the effect of a nanosecond plasma actuator was simulated as an instantaneous energy release distributed in space. Good agreement between the simulation results and experimental data on a flow separation control indicates that there is no noticeable effect of the slow relaxation of the energy of vibrational degrees of freedom on the process.
In particular, in [226], a good agreement was obtained with the results of experiment [219] on the pressure distribution over the surface of airfoil (Fig. 53) for different variants of calculation with instantaneous volumetric energy release (V1–V3 in Fig. 53). It should be noted that purely surface heating (variant S) gives a noticeably underestimated efficiency of flow separation control. This conclusion is confirmed by the data of [210] (Fig. 48) and analysis in [216], where the wall heating and the shock wave generation were considered as energy loss channels that reduce the actuator efficiency.
In [227], similar results were obtained for a flow with a Reynolds number Re = 1.15 × 106 (Fig. 54). The airfoil chord length was c = 0.2032 m, the free-stream flow velocity was U∞ = 93 m/s, and the angle of attack was α = 20°. The peak voltage of high-voltage pulse was Vpeak = 8.4 kV. The pulse repetition rate was 915 Hz for this mode, which leads to a dimensionless frequency \(F_{c}^{ + }\) = fc/U∞ ≃ 2. It was assumed that 35% of the pulse energy (0.092 mJ/cm) passes into fast heating of gas in the discharge and the energy release time is τ = 100 ns. The length and thickness of the plasma layer were taken to be 5 and 0.4 mm, respectively. The dynamics of vortex development and flow reattachment calculated in this work qualitatively reproduces the result of experiment [215] (Fig. 52). Thus, the mechanism of fast heating of gas during the decay of a ns-SDBD plasma makes it possible to fully explain the development of perturbations in the mixing layer at the boundary of the separation zone, momentum transfer to the airfoil surface, and flow reattachment.
Vorticity contours for two values of the reduced time t+ after a single action of the ns-SDBD actuator at Re = 1.15 × 106 [227].
10.3 Effect of Actuator Position on Efficiency of Flow Control
It must be admitted that there have been practically no systematic studies of the effect of the actuator position on the efficiency of suppression of flow separation. Early work on a flow control using AC-SDBD postulated an increase in the flow velocity in the boundary layer as the main mechanism for such a control. This approach led to the conclusion that the actuator can be effective both when located in front of the separation zone and directly in the separation vortex region. On the other hand, it is obvious that a ns-SDBD actuator that cannot generate a near-wall jet will be inefficient in the separation zone. In [207], for nanosecond actuators, an arrangement typical for the AC mode was used: the actuators were located in several rows at different distances from the leading edge. However, already in [208], two alternative configurations of electrodes were investigated: with an arrangement parallel and perpendicular to the leading edge (Fig. 55). It was shown that, in the second case, the efficiency of the actuator is noticeably higher than in the first, and it was concluded that, for flow regimes with a fixed angle of attack of the airfoil, the actuator located in front of the flow separation point is much more efficient.
(Top) Various electrode configurations for the ns-SDBD actuator and (bottom) static pressure distribution over the airfoil surface; angle of attack α = 17°; U∞ = 110 m/s; pulse duration 25 ns; voltage 25 kV. (Left) The electrodes are parallel to the leading edge; (right) the electrodes are perpendicular to the leading edge [208].
A typical example of the dependence of the efficiency of an actuator on its position on the airfoil is the comparison of the results of [212, 228], where the control of transonic flow separation using ns-SDBD actuators was studied. In [212], the actuator was located at the leading edge of the airfoil, which provided a strong flow response to the actuation (Fig. 51a). In later works [228, 229], the actuator was located in the center of the airfoil, practically in the region of a buffet pressure shock. In contrast to [212], in [228, 229], the effect of the actuator on the pressure distribution over the airfoil surface in transonic modes was practically not found. Thus, for the efficient operation of the ns-SDBD actuator, it should be placed near or directly on the leading edge of the airfoil. It is worth noting the opposite to the standard configuration of the electrode system. The exposed electrode is moved downstream with respect to the insulated one, which leads to the development of a discharge from the leading edge of the exposed electrode upstream.
The placement of the actuator on the leading edge, however, is difficult when the wing size is large. The scaling problem is that the perturbation generated by the actuator rapidly decays with increasing distance from the electrodes due to diffusion and thermal conductivity. Since the separation point can move along the chord, depending on the chosen airfoil, angle of attack, and velocity, it is tempting to use several successive electrode systems to ensure that the perturbations fall within the required range of distances from the separation point. In [230], the effect of nanosecond actuators on large-scale flow reattachment to the wing of the EAGLET EE-10 aircraft was demonstrated experimentally. One wing panel of this aircraft (maximum thickness 25 cm, length more than 300 cm, average chord 120 cm, NACA 63-415 airfoil) was fixed on a static stand in a TU Delft wind tunnel (Fig. 56). The wing was at a substantially supercritical angle of attack α = 27°. The Reynolds number calculated from the chord of the airfoil was Re = 2.4 × 106. The actuators were located on the airfoil in six positions: at the leading edge and at a distance of 15, 20, 30, 40, and 50 cm downstream. In this case, the first three actuators were made for the entire length of the panel, and the next three, for a half (Fig. 56).
(Top) EAGLET EE-10 aircraft; (bottom): visualization of flow separation by the filament method for a NACA 63-415 airfoil at a velocity of 30 m/s, an angle of attack of 27°, and Rec = 2.4 × 106 [230]. (Left) Actuators are off and (right) actuators are on. (Inserts) enlarged images of the visualization of near-wall flow using filaments; (left) the actuator is off, the near-wall flow is directed against the flow; (right) the actuator is turned on and the near-wall flow is directed along the main flow.
It is clearly seen that, when the actuators are turned off, the flow detaches from the wing almost immediately behind the leading edge (Fig. 56, left). Turning on the actuators resulted in flow reattachment. In this case, the presence of three additional actuators downstream improved the flow quality (Fig. 56, right). Thus, for high Reynolds numbers and long chords, the use of multiple actuators one after the other makes it possible to improve flow control. At the same time, the position of the first actuator should be close to the leading edge of the wing.
In [231], it was proposed to place this first actuator even more upstream, so that the edge of the high-voltage electrode coincide with the leading edge of the profile and the entire discharge develops on its lower surface (Fig. 57). In this case, at positive angles of attack, the stagnation point of the flow shifts to the lower surface of the airfoil and turns out to be further upstream than the zone of maximum discharge energy deposition, which is located near the leading edge of the exposed electrode. This ensures that the perturbation created by the actuator is carried to the flow separation point at any positive angles of attack. With this position of the actuator, no reduction in lift is observed at high angles of attack, and the maximum excess of lift in comparison with experiments with the actuator turned off reaches the values of CL(ON)/CL(OFF) ~ 2.14 (Fig. 58).
Schematic of the placement of an ns-SDBD actuator on the airfoil [231].
Lift coefficient vs. the angle of attack [231]. The power of the plasma actuator is 0.08 W/cm, the pulse frequency is f = 150 Hz, the energy per pulse is 0.6 mJ/cm, and the flow velocity is 31 m/s; NACA-0015 airfoil, chord length 15 cm, Re = 3.06 × 105, and \(F_{c}^{ + } = 0.73\).
In contrast to [213, 231], in [232, 233] the actuator was used in the standard geometry: the exposed electrode was located upstream and the encapsulated electrode was located downstream. The trailing edge of the exposed electrode, from which the discharge started, was not on the airfoil axis, but shifted from the leading edge by 0.5% of the chord. Since, in [232, 233], the NACA-0015 airfoil was also used at practically the same Reynolds numbers (Re = 3.06 × 105 for [231] and Re = 2.68 × 105 for [233]), it becomes possible to directly compare the efficiency of these two geometries of ns-SDBD actuators. Shown in Fig. 59, the results of measurements of the lift coefficient in [233] demonstrate its noticeable reduction at angles of attack higher than α = 22°, while, for the configuration [231], a steady increase in CL is observed at least up to the angle of attack α = 25°. The maximum increase in the lift in [233] after turning on the actuator reaches only CL(ON)/CL(OFF) ~ 1.61 (in [231], CL(ON)/CL(OFF) ~ 2.14). It should also be noted that, in [233], in order to achieve a noticeably weaker effect, a higher operating frequency of the actuator was needed (\(F_{c}^{ + } = 2.96\) [233] and \(F_{c}^{ + } = 0.73\) in [231]). Thus, the position and geometry of an actuator have a significant effect on its efficiency. Apparently, it can be stated that the optimal position of the zone of maximum energy release of the ns-SDBD is located near the central point of the airfoil at its leading edge. Placing the nanosecond actuator at the top surface of the profile reduces its efficiency. The only option where the use of such actuators becomes appropriate is when such actuators are used in combination with an actuator on the leading edge in order to enhance its efficiency on large airfoils and/or in the case of dynamic flow separation, which will be discussed in the next section.
Effect of an ns-SDBD on lift and drag coefficients vs. the angle of attack α: (a) CL; (b) CD at Re = 2.68 × 105 and \(F_{c}^{ + } = 2.96\) [233].
It should be noted that the maximum efficiency of an ns-SDBD actuator was also noticed near \(F_{c}^{ + } = 1.0\) [234]. At the same time, in [235], when studying the separation flow control on the Boeing Vertol VR7 airfoil, the actuator was located at \(x{\text{/}}c = 0.04\). At comparable Reynolds numbers Re = (0.217–0.307) × 106, even for a reduced frequency \(F_{c}^{ + } = 4.21\), only partial flow reattachment was observed. The difference from the results of [231, 234] was explained by a significant difference in the character of the airfoil, especially near the leading edge. This explanation is partly correct, but the main difference lies in the shift of the actuator in [235] downstream, where the energy release zone partially falls behind the flow separation line and the operation of the actuator becomes less efficient.
11 CONTROL OF DYNAMIC FLOW SEPARATION
The problem of controlling the dynamic flow separation is important because, in practice, any separated flow is unsteady. This also applies to airplanes that reach supercritical angles of attack only for a very short time, comparable to the flow reattachment time; to helicopters, where, at high flight velocities, the problem of flow separation from the retreating blade becomes important; and to wind turbines, where a sharp gust of wind can disrupt the flow from the blades before the rotor changes direction in space and rotation velocity. Despite this, the problem of dynamic flow control using pulsed discharges has been considered only in a few works because of its complexity.
Apparently, one of the first works where an attempt was made to control dynamic flow separation using an ns-SDBD was [236]. A NACA-0015 airfoil installed in a transonic wind tunnel was used. The angle of attack varied in a sinusoidal manner. The reduced frequency of the actuator was in the range of \(F_{c}^{ + } = 0.78\)–6.06 for М = 0.2 and from 0.39 to 2.03 for М = 0.4. Despite the fact that in the work [236] an optimistic conclusion was made about the possibility of dynamic separation control under such conditions, no significant changes in the lift coefficient and its distribution over the airfoil were found (Fig. 60). Possibly, the weak effect of the actuator on the flow was associated both with a high level of initial perturbations in the wind tunnel [236] (the flow separation on a fixed airfoil was not detected up to an angle of attack α = 16°) and with an unfavorable location of the actuator at 4% of the airfoil chord—far from the leading edge.
(a) Lift coefficient (CL) and (b) moment coefficient (CM) vs. the angle of attack [236] at M = 0.4, k = 0.05, F+ = 2.03, and Re = 2.2 × 106. The curves correspond to measurements with the actuator turned off and on.
11.1 Flow Reattachment Dynamics
The ability to control dynamic flow separation depends on the flow reattachment time τatt after turning on the actuator. Obviously, under the condition \({{\tau }_{{{\text{att}}}}} \ll 1{\text{/}}f\), where f is the frequency of variation in the angle of attack, the problem of dynamic separation control will not differ significantly from the problem of static separation control. Thus, the key question is the speed of the system’s response to the action of the actuator.
This issue was investigated in [237], where direct measurements of forces and moments acting on a NACA-0015 model airfoil were carried out with dynamic switching on and off of the actuator located on its leading edge. Measurements have shown (Fig. 61) that the static separation of the flow on the NACA-0015 airfoil occurs at an angle of attack α > 12°, which is in good agreement with the known data. In this case, the lift of the airfoil decreases almost by a factor of 1.8, while the drag force increases. As can be seen from the data [237], turning on the actuator even at a low reduced frequency \(F_{c}^{ + } = 0.725\) leads to the reattachment of the flow and an increase in the lift up to a value exceeding the lift at the critical angle of attack by 20% (Fig. 61).
(a) Dynamics of flow reattachment and variation in lift [237]: lift for different angles of attack. The first pulse of the actuator occurs at t = 0 s. Mean discharge power P = 2 W, pulse repetition rate f = 150 Hz (\(F_{c}^{ + } = 0.725\)), pulse energy Q = 15 mJ. Lift vs. the number of pulses in a burst. U∞ = 31 m/s, f = 200 Hz (F+ = 0.97): α = (b) 16°; (c) 20°; and (d) 26°; NACA-0015 airfoil, c = 15 cm.
Another important result of [237] is that flow reattachment mechanism is independent of the presence or absence of subsequent pulses in the burst. As a rule, even the first pulse of the actuator causes a reattachment of the flow, and an increase in the lift. Subsequently, at relatively small angles of attack, this flow configuration preserved for a rather long time (Fig. 61). Only at the maximum angles of attack investigated in [237] (α = 26°), the flow separated again practically at the moment of the end of the actuation.
An indicative factor is the rate of change in the lift of the airfoil. It was established in [237] that the flow reattachment time did not exceed few milliseconds after turning on the actuator (Fig. 62). It should be noted that this time noticeably decreases with increasing angle of attack. Apparently, this reduction in the system reattachment time in this range of parameters is associated with an increase in the tangential discontinuity at the boundary between the separation bubble and the main flow, which leads to a more rapid development of perturbations in it, more intense vortex formation in this layer, and the destruction of the separation vortex. The ratio of the flow reattachment time to the characteristic time of the change in the angle of attack of the airfoil (τatt f) calculated from these data shows that, in a wide range of unsteady flows at a reduced frequency k < 0.2, the condition \({{\tau }_{{{\text{att}}}}}f \ll 1\) is satisfied, which guarantees that the flow will have time to reattach to the airfoil despite the change in the angle of attack with time (Fig. 62).
Flow reattachment time vs. the angle of attack (left). Reduced flow reattachment time vs. reduced frequency of variation in the angle of attack, k = πfc/U∞ (right) according to [237]. Discharge power P = 3 W, f = 225 Hz (F+ = 0.75), Q = 15 mJ/pulse, and U∞ = 44.7 m/s; NACA-0015 airfoil.
11.2 Controlling the Dynamic Separation of the Direct Flow
The first demonstration of the control of the dynamic separation of the flow around an airfoil was made in [238, 239]. In these works, both single and multi-electrode actuators were used. The single actuator was positioned so that the edge of the high-voltage electrode coincided with the central line of the airfoil at the leading edge (Fig. 57). An increase in the lift of the airfoil was demonstrated for significantly supercritical angles of attack and reduced frequencies k = π f c/U∞ = 0–0.05 in the range of velocities U∞ = 30–45 m/s (Re = (3–4.5) × 105).
It was shown that the use of a plasma actuator can prevent a sharp decrease in lift and an increase in drag even when the maximum angle of attack of the blade increases to α = 32°. Turning on the actuator resulted in an instant increase in lift by as much as 55%. This makes it possible to significantly expand the flight envelope and improve the controllability of helicopters in critical regimes.
Figure 63 shows the dynamics of the lift of the airfoil when the angle of attack varies from αmin = 0° to the maximum angle αmax = 26°. It can be seen that, due to the dynamic character of the interaction, the lift reduction begins much later than the critical angle of attack for a given airfoil αcrit = 12° is reached. After reaching the angle α = 16°, flow separation begins (the delay from the point of passing the critical angle is about 30 ms).
Dynamics of lift during a cycle of variation in the angle of attack [238], αmax = 26°, sinusoidal profile with a period t = 575 ms (k = 0.026). U∞ = 31 m/s (Re = 3 × 105). The actuator switching frequency is f = 167 Hz (F+ = 0.81). The marks “Start” and “End” indicate the actuator operation region.
The displacement of the separation point upstream leads to a complete separation of the flow and a sharp drop in the lift. Up to this moment, the presence of an actuator does not affect the development of the flow, since its operation needs a formed separation bubble with a shear layer, where the perturbation created by the actuator can develop. The development of such a bubble takes approximately the same time as the delay of flow separation: 30 ms. After that, the development of the flow becomes fundamentally different for the case without and with the action of the actuator. In the case without a discharge, the development of flow separation leads to a sharp catastrophic drop in the lift force (by 40% of the maximum value before the flow separation). In the case of excitation by the actuator, the drop in lift is practically absent and it remains at a level close to the value reached at the moment of flow separation. In the experiment shown in Fig. 63, the actuator was forcibly turned off after the airfoil reached the maximum angle of attack (t = 330 ms) in order to trace the effect of the actuator on the amplitude and rate of changes in lift in the separation regime. From the data in Fig. 63, it can be seen that the lift oscillation frequency decreased slightly (70 Hz and 60 Hz with the actuator turned on and off, respectively), while the oscillation amplitude almost doubled. At the same time, a transition to a separated flow began, which did not have time to complete before the angle of attack decreased to subcritical values (Fig. 63). After the angle of attack decreased to α < 12°, a natural reattachment of the flow occurs, and the lift becomes the same as at the corresponding angles of attack on the ascending branch of the cycle.
To assess the efficiency of suppressing the dynamic separation, in [238] the integral-over-cycle change in the lift of the actuator as function of the frequency of the action was measured (Fig. 64). The maximum efficiency falls within the range \(F_{c}^{ + } = 0.5{-} 1.0\), which is in good agreement with the data on controlling the static flow separation and estimates of the flow reattachment time (see Fig. 62). In addition to the data on a single actuator located at the leading edge of the airfoil, in [238], experiments were carried out with a multi-electrode actuator configuration of the type shown in Fig. 56. The multi-electrode configuration used the same electrode at the leading edge of the airfoil plus four additional electrode pairs uniformly distributed over the top surface of the airfoil in parallel to the leading edge. The distance between the electrodes was 30 mm. It was assumed that such additional electrodes can influence the dynamics of the separation flow as the separation point moves forward from the trailing edge of the wing. It can be seen from the data [238] that the integral increase in lift reaches 15% in the case of a single electrode at the leading edge and increases to 20% in the case of a multi-electrode system. Thus, it was shown that the maximum effect on the flow is achieved with the actuator located at the leading edge. The actuators located downstream increase the lift only a little by interacting with the separation zone at the moments when a separation zone is downstream of a given electrode pair.
Lift integrated over the cycle of variation in the angle of attack vs. the reduced actuator frequency. F/F0 is the ratio of the integral of the lift with the actuator on to the integral without an actuator. αmax = 20° and 26°, sinusoidal profile of variation in the angle of attack with a period t = 575 ms (k = 0.026). U∞ = 31 m/s (Re = 3 × 105) according to [238].
In recent papers [234, 240], the authors copied the arrangement and geometry of ns-SDBD actuators proposed in [237–239]. In this case, the conclusions of [238, 239] on the high efficiency of such an arrangement of actuators were fully confirmed. In [234], using an asymmetric airfoil with a relative thickness of 12% in a flow at a velocity of U∞ = 50 m/s, the effect of an actuator on a separated flow arising when the angle of attack of the airfoil changes periodically in the range α = 10°–20° at a reduced pitch frequency k = 0.012–0.1 was studied. It has been shown that, at a frequency of the actuation \(F_{c}^{ + } = 0.13{-} 0.96\), an ns-SDBD actuator can reduce the hysteresis of the aerodynamic coefficients and, in all cases, the effect of flow control was achieved (Fig. 65).
Dynamics of lift for different reduced pitch frequencies of the airfoil angle of attack [234]; regimes (a) without and (b) with excitation of the ns-SDBD actuator, respectively.
In [240], the use of plasma ns-SDBD actuators for dynamic flow control at relatively small angles of attack α = 10°–16° was considered to study the weak separation regime. The reduced pitch frequency (k) and the excitation Strouhal number (Ste) were varied for a Reynolds number Re = 3 × 105 in the ranges k = 0.05–0.1 and Ste = 0–13.4. In all cases, a significant increase in the lift-to-drag ratio was observed. It was also noticed that, in all cases with active control, earlier flow reattachment and a reduction in the lift hysteresis were observed (Fig. 66).
Low separation mode [240]: (a) lift coefficient and (b) drag coefficient for k = 0.075, Re = 3 × 105, and various excitation frequencies Ste. The angle of attack varied according to the law α(t) = 10° + 6°sin(ωt). The case of Ste = 0 corresponds to a switched off actuator.
11.3 Controlling the Dynamic Separation of the Reverse Flow
At high flight velocities of a helicopter, in addition to the problem of dynamic flow separation on the retreating blade due to its high angle of attack, another problem arises. This is the problem of reverse flow around the root parts of the retreating blade. Due to the high angle of attack of this blade when it moves with a sharp edge forward relative to the incoming air, an intense flow separation occurs almost inevitably. Since the velocity of the root parts of the blade is low, they do not significantly affect the lift. On the other hand, the separation from the sharp edge of the blade leads to strong vibrations and noise. For this reason, the ability to control this separation becomes very important.
For the first time, the feasibility of controlling the flow separation on the retreating blade was demonstrated in [238, 239]. A NACA-0015 airfoil was turned in the wind tunnel so that the flow moved from the sharp trailing edge of the airfoil to the leading edge (Fig. 67). In this case, the same principle was used as in the case with the normal direction of the flow (Fig. 57): the edge of the high-voltage electrode was located exactly on the airfoil axis at the trailing edge and the discharge developed on the pressure side of the airfoil.
To demonstrate the static characteristics of reverse flow separation, Fig. 68a shows the regime of slowly varying angle of attack. An actuator with a pulse energy of about 0.6 mJ per centimeter of the wingspan continuously operated in the first half of the cycle and was turned off in the second. It is clearly seen that, in the absence of excitation, the flow separation pattern is symmetric, which indicates a quasi-stationary character of separation. In this case, the flow separation occurs already at an angle of attack α = 9° due to the presence of a sharp leading edge. A further increase in the angle of attack leads to an increase in the separation zone; in this case, up to α = 15° the lift decreases. A reduction in the angle of attack from the maximum value leads to a mirror-symmetric pattern of the recovery of a fully attached flow at α < 9° (Fig. 68a).
Dynamics of lift during the cycle [239]. (a) Reverse flow, U∞ = –31 m/s: slow change in the angle of attack—control of the static separation of the flow from the sharp edge. The plasma actuator was turned on during the first half of the cycle; rapid change in the angle of attack—control of dynamic flow separation from the sharp edge: αmax = (b) 11.5°; (c) 17°; and (d) 23°. The plasma actuator is on during the entire cycle. The pulse energy is Q = 0.6 mJ/cm.
Figures 68b–68d shows the effect of the actuator on the dynamic separation at the reduced frequency k = 0.026 and the actuator’s reduced frequency \(F_{c}^{ + } = 0.6\) for various angles of attack. It is seen that, for αmax = 11.5°, the effect of the actuator completely eliminates the flow separation. At large angles of attack αmax = 17° and 23°, the flow separation occurs much later than in the variant with the actuator turned off. The lift monotonically increases with increasing angle of attack until flow separation occurs (α ~ 10°). The reattachment of the flow occurs in the phase of the reverse motion at smaller angles (α ~ 6°–8°) due to the nonstationarity of the process. At high angles of attack (Figs. 68c and 68d), partial reattachment occurs with a two-fold increase in the lift. The period-integrated lift, as seen in Fig. 69, increases monotonically with the actuator turned on up to the maximum angles αmax = 32° with a relative increase in lift up to 55%, while variations in drag remain below 10%.
Integral of (a) lift and (b) drag over a period of variation in the angle of attack for the configuration with reverse flow [239]; U∞ = 31 m/s, k = 0.026, and \(F_{c}^{ + } = 0.53\).
Thus, it has been found that an ns-SDBD actuator is effective both in controlling the dynamic flow separation from a blunt leading edge with a large radius of curvature and in controlling the reverse flow separation from sharpened edges. The conditions for the effective operation of the actuator are (a) its location directly on the leading edge of the airfoil (Figs. 57, 67); (b) sufficient energy of the discharge pulse, which, apparently, depends on the Reynolds number of the flow and, for moderate values of Re = 3 × 105, is close to Q ~ 1 mJ/cm; and (c) operation of the actuator in the effective range of reduced frequencies \(F_{c}^{ + } = \) \({{F}_{f}}c{\text{/}}{{U}_{\infty }}\) ~ 0.5–1.0.
11.4 Control of 3D Flow Separation
To study the efficiency of plasma actuators in a three-dimensional flow, a special series of experiments with a helicopter model was carried out in [241] (Fig. 70). For the experiment, a standard radio-controlled helicopter model (ALIGN TREX 800E) was used. The model was equipped with a 4.5 kW electric motor. The model was additionally equipped with an electrical system to supply high-voltage nanosecond pulses from a FID 20-10 generator to rotating blades. The pulses had an amplitude of 20 kV and a frequency of 200 Hz to 2 kHz. Asymmetric plasma actuators (layout as in Fig. 57) were installed at the leading edge of the blades. Electrodes were spread along the entire length of the leading edge. The rotor blade span was 1860 mm, and the blade chord length was 60 mm. In all cases, the blades rotated at a frequency of ~18 Hz.
Model of a helicopter on the scales [241].
Figure 71a shows the dependence of the lift force of a rotating rotor at a fixed angle of attack on the actuator frequency. The almost linear increase in lift for the actuator frequency range 300–1500 Hz reflects the fact that different parts of the blades have different linear velocity and the optimal response frequency increases with increasing distance from the rotor axis. The outer parts of the blades create a larger lift, and an increase in the actuator frequency leads to an increase in the total lift, since the optimal point (\(F_{c}^{ + }\sim 1\)) shifts with an increase in the actuator frequency to the tips of the blades.
(a) Lift vs. actuator frequency [241]; angle of attack is α =20° and (b) lift vs. the angle of attack. \(F_{c}^{ + } = 0.57\) (1 kHz); \(F_{c}^{ + } = 1.14\) (2 kHz).
Figure 71b shows the results of measurements of the lift force in a static regime at various angles of attack in three cases: with the actuators turned off, at a discharge frequency f = 1 kHz (\(F_{c}^{ + } = 0.57\)), and at a discharge frequency f = 2 kHz (\(F_{c}^{ + } = 1.14\)). Without actuators, the maximum lift is achieved at α = 12°. A further increase in the angle of attack leads to flow separation on the blades and lift force reduction (Fig. 71b). When the actuator was turned on, a significant increase in lift was observed at higher angles of attack (α = 20°) compared to the maximum lift obtained with the actuators turned off: up to 7% increase for the actuator frequency \(F_{c}^{ + } = 0.57\) and up to 20% increase at \(F_{c}^{ + } = 1.14\).
At a discharge power of ~38 W (\(F_{c}^{ + } = 1.14\), f = 2 kHz), an increase in the integral lift was achieved by more than 20% at a constant motor power of 1500 W compared to the optimal blade configuration without actuators. These results show the high efficiency of using actuators for three-dimensional flows and open up the possibility of their use for real helicopter systems.
12 DE-ICING PLASMA SYSTEMS
The practical application of plasma systems to control the aircraft motion in the atmosphere sometimes encounters the objection that electric discharge systems can be unstable in the conditions of rain or snow. Indeed, as a result of the formation of a continuous thick water or ice layer on the electrode surface, it may happen that the discharge will not develop and the actuator will stop working. However, the formation of such a thick water film on the surface of a wing moving at high speed is impossible. The water will be carried away by the air stream, and individual drops and jets will not affect the actuator efficiency.
Ice formation on the wing surface is a more difficult issue. In this case, the ice layer can accumulate and block the formation of the plasma layer. Usually, de-icing of the wing and other structural elements of the aircraft is performed using heating elements built into the structure. It should be noted that the presence of a plasma actuator does not reduce the functionality of such devices. If the standard de-icing system of an airplane or helicopter can cope with ice formation, it will automatically clean up the actuator electrode system as well. However, plasma actuators are heat sources by themselves. It is interesting to check whether such actuators can simultaneously work as a de-icing system.
Compared to a conventional de-icing system based on heating the airfoil surface, a de-icing system based on plasma actuators can have significant advantages. First, plasma actuators initially heat up not the structural elements of the wing, but the air in the boundary layer; second, strong perturbations (shock waves) created by such actuators can lead to mechanical, rather than thermal, removal of emerging ice elements from the surface; third, such actuators do not require space inside the wing for their placement and are lightweight.
In [242, 243], the thermal characteristics of an ns-SDBD plasma on the surface of the airfoil were studied and the de-icing characteristics of such plasma actuators were estimated. A number of experiments were carried out to assess the effect of various environmental parameters on the efficiency of gas heating under the action of an ns-SDBD. Using a high-speed imaging system and infrared imaging with synchronization in time and spatial resolution, the transient thermal characteristics of the plasma above the wing surface and the de-icing characteristics of an ns-SDBD were studied. These characteristics were estimated under various icing conditions: frost, mixed conditions, and ice glaze. The influence of the velocity of the incoming air flow, the air temperature, and the angle of attack of the model on the icing rate was investigated. It was found that the de-icing characteristics of plasma actuators significantly improve with an increase in the discharge repetition rate, which is an obvious consequence of an increase in the mean power released by the discharge into the translational degrees of freedom of the gas.
Figure 72 shows a schematic of the model used in the ns-SDBD icing control experiment. The model was divided into two symmetrical halves, on which identical actuators were mounted. The actuators on one of the halves were connected to a source of nanosecond high-voltage pulses; the other half of the model served as a control sample. The temperature distribution over the wing surface was measured under icing conditions when the plasma actuator was operating at various frequencies, and it was shown that, at a high operating frequency of the actuator, the energy released by it is sufficient not only to heat the near-surface layer of air, but also to heat the surface itself by several degrees.
Schematic of the model and airfoil used in the experiment on icing control using an ns-SDBD [242].
Pulse heating of air in the boundary layer near the leading edge of the airfoil leads to the formation of shock waves, which contribute to the mechanical removal of ice from the airfoil surface. In addition, a warm layer forming near the surface prevents ice particles and water droplets from refreezing on the wing surface downstream (Fig. 73). It is clearly seen that, at a high actuator’s pulse repetition rate, practically no ice accretion on the surface occurs. In [244, 245], the results of [242, 243] were confirmed using the longitudinal arrangement of the electrodes of a nanosecond actuator, similar to that used in [212] to control the boundary layer separation in transonic regimes (Fig. 74). The results obtained in [242–245] show, first of all, a significant stability of the operation of ns-SDBD plasma actuators in the presence of a large amount of water and ice and snow particles in the incoming flow, as well as the prospects for the development of new plasma-assisted strategies of de-icing, specially designed to reduce the icing of aircraft in flight conditions.
Time evolution of the dynamic processes of ice accretion on the airfoil surface under icing conditions at U∞ = 40 m/s, liquid water flow rate 1.0 g/m3, and T∞ = –10°C [243]. The ns-SDBD actuator operated at a frequency of f = (a) 2, (b) 4, and (c) 6 kHz.
Images for 3 min (time is indicated on the frames) from the beginning of the dynamic de-icing process using a nanosecond plasma actuator under the following conditions: discharge frequency f = 6 kHz, voltage V = 7.7 kV, electrode length 0.484 m, liquid water flow rate Q = 0.5 g/m3, average droplet diameter d = 25 µm, T = –15°C, and U∞ = 65 m/s [244].
13 CONCLUSIONS
This review demonstrates the enormous potential for controlling high-speed gas flows by means of ultrafast local heating of the medium during the creation and decay of a highly nonequilibrium pulsed plasma. It was shown that such local heating makes it possible to control the configuration of shock waves in a supersonic flow, the shock wave–boundary layer interaction, and is effective both at low subsonic and supersonic velocities. The use of plasma makes it possible to control both static and dynamic flow separation at high angles of attack, including the reverse flow regime, which is typical of a retreating helicopter blade. Of considerable interest are recent works on the control of turbulent drag and laminar–turbulent transition.
The main factors for obtaining high efficiency of flow control using plasma actuators is their placement relative to key points of the airfoil and the flow. In particular, for controlling the motion of a supersonic object, the spreading of the profile of the generated perturbation along the trajectory of motion and its significant amplitude, which depends on the Mach number and the angle of inclination of the leading shock wave, are critical. Effective control of boundary layer separation by means of pulsed energy release is possible if the actuators are placed directly on the leading edge of the airfoil in front of the flow separation point. Controlling the dynamics of the mixing layer is most effective when the actuators are placed on the boundary or in the layer.
Another important aspect of plasma flow control is the actuator’s operating frequency. Numerous experiments have shown that effective flow control is highly dependent on the frequency of the action. In the case of separated flows, the most effective frequencies correspond to the Strouhal number on the order of unity. On the contrary, for de-icing systems, such a low frequency is ineffective due to the low mean power, and the required frequency range in this case is much higher. The control of supersonic motion leads to a noticeable redistribution of loads on the flying object, while the perturbation created by the discharge moves along its surface. Thus, to effectively influence the configuration of shock waves and the loads created by them, the range of Strouhal numbers should also be on the order of unity.
An important point is the actuator’s pulse energy. It should be noted that all considered cases do not imply a change in the global flow parameters (e.g., a change in the velocity of the flow as a whole or its heating) with the help of plasma. On the contrary, the discharge energy is always used pointwise, only to create either an inhomogeneity of the field of flow parameters or as an initiator of the instability development in the main flow or the layer. This approach does not require significant energy even to control a supersonic flow around objects with a high aerodynamic quality and makes possible an effective de-icing of aerodynamic surfaces, and, with a low power of the control action, effective control of the static and dynamic flow separation at high velocities and significantly supercritical angles of attack.
From such an analysis, it becomes obvious that the effective use of plasma actuators is determined by the ability to control the rate, position, and intensity of energy release in the plasma. This review considers the main mechanisms of the fast generation of a strongly nonequilibrium plasma in high-speed gas flows. As a rule, such mechanisms include pulsed discharges at high and ultrahigh overvoltage. A significant excess of the electric field over the threshold value allows fast heating of the electronic ensemble. With a constant direction of the electric field (e.g., in nanosecond pulsed discharges), this leads to the fast achievement of the ionization threshold by electrons and the efficient formation of a strongly nonequilibrium plasma. In the case of an alternating field, microwave or laser, the time between electron-molecule collisions and the time of changing the direction of the field, depending on the conditions, can become comparable. Under these conditions, for electrons to reach the ionization energy and avalanches to develop, a large number of cycles may be required, and the electric field must be much higher than in the case of a pulsed nanosecond discharge. It should be noted that, for any type of discharge, the key factor of its applicability for flow control due to pulsed localized energy release is the possibility of creating a relatively dense plasma with a typical specific energy deposition of 0.05–0.5 eV per molecule in the electronic degrees of freedom of the gas and ionization in a time shorter than the time of the gasdynamic expansion of the plasma region.
The requirement for the dominant direction of the discharge energy deposition to the excitation of high-energy states is dictated by the need for fast conversion of the excitation of the internal and chemical degrees of freedom of the gas into thermal energy, which can be used to flow control. Experiments have shown that the highest efficiency and rate of such energy relaxation in the sequence of events “application of an electric field–electron heating–excitation and ionization of molecules–thermalization of energy” is achieved precisely at high and ultrahigh electric fields, when the dominant type of gas excitation is the formation of electronically excited states of molecules and ionization. In this case, fast quenching of highly excited particles and plasma recombination lead to the formation of translationally hot atoms and molecules, which transfer their energy to the rest of the gas in several collisions. This situation is fundamentally different from excitation, e.g., of the vibrational degrees of freedom of molecules at moderate electric fields, when the relaxation of excitation and an increase in the gas temperature can take a long time from the viewpoint of gas dynamics.
In conclusion, let us mention the unsolved problems of plasma-assisted flow control. The first, of course, are the weather conditions. Despite the direct experimental demonstrations of the possibility to successfully operate for plasma actuators even under severe icing conditions, questions remain about the possible reduction in the effectiveness of such systems in the presence of heavy rain, snow, or dusty air. Another important aspect of the problem, which limits the possibilities of using plasma actuators, is the electromagnetic noise they create. As already noted, the most effective are pulsed systems that generate a highly excited plasma in a few to tens of nanoseconds. Since the efficiency of radiation of an electromagnetic signal by any conductor, as a rule, sharply increases with increasing frequency, an increase in the efficiency of plasma systems inevitably means an increase in electromagnetic interference created by them. In addition, the issues of stability of such systems under the action of atmospheric electricity have hardly been investigated. In the case of a laser pulse-initiated optical breakdown, the laser system can always be reliably shielded from the lightning current, but it is much more difficult to protect the electrodes of SDBD actuators and pulse voltage generators. The same group of unresolved issues includes the mass-dimensional and energy characteristics of plasma actuators. Despite their relatively low power consumption, the required range of supplied power can reach, depending on the size of the object, several kilowatts. For laser systems, due to the low coefficient of conversion of electricity to beam energy and then to plasma, the required power on board the aircraft can be even higher. In conclusion, let us mention a purely technological problem. The best characteristics in terms of wear resistance, chemical resistance, electrical insulation parameters, and their stability is exhibited by electrotechnical ceramics. However, such materials are brittle and their machining is difficult. Dielectric polymer films used in laboratory conditions (Kapton®, PVC, PTFE®) provide a unique dielectric strength of the layer, high chemical and physical stability, but have a noticeably lower wear resistance compared to ceramics, which imposes certain restrictions on their use in conditions of dusty flows.
Resolving these issues will open up completely new possibilities for ultrafast control of flows and high-speed objects by means of a highly nonequilibrium pulsed discharge plasma.
REFERENCES
P. Bletzinger, B. N. Ganguly, D. Van Wie, and A. Garscadden, J. Phys. D: Appl. Phys. 38, R33 (2005).
E. Moreau, J. Phys. D: Appl. Phys. 40, 605 (2007).
R. B. Miles, Plasma Flow Control, Fundamentals, Modeling, and Applications (Lecture Series Notes for Von Karman Institute Lectures) (Von Karman Institute for Fluid Dynamics, Sint-Genesius-Rode, 2011).
A. V. Boiko, A. V. Dovgal, Y. B. Zanin, and V. V. Kozlov, Termofiz. Aeromekh. 3 (1), 1 (1996).
A. M. Mhitaryan, S. D. Labinov, and V. Ya. Fridland, Some Problems of Aerodynamics and Electro-Hydrodynamics (Kiev. Inst. Inzh. Grazhdanskoi Aviats., Kiev, 1964), Vol. 1, p. 3 [in Russian].
A. M. Mhitaryan, V. S. Maksimov, V. Ya. Fridland, and S. D. Labinov, Inzh.-Fiz. Zh. 4 (9), 12 (1961).
A. I. Klimov, A. N. Koblov, G. I. Mishin, Yu. L. Serov, and I. P. Yavor, Sov. Tech. Phys. Lett. 8, 192 (1982).
J. R. Roth, Phys. Plasmas 10, 2117 (2003).
J. R. Roth, in IEEE Conference Record—Abstracts: 1998 IEEE International Conference on Plasma Science (IEEE Press, New York, 1998), p. 291.
J. R. Roth and X. Dai, in Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2006, Paper AIAA 2006-1203.
J. R. Roth, D. M. Sherman, and S. P. Wilkinson, in Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 1998, Paper AIAA 1998-0328.
J. R. Roth, D. M. Sherman, and S. P. Wilkinson, AIAA J. 38, 1166 (2000).
A. P. Bedin and G. I. Mishin, Tech. Phys. Lett. 21, 5 (1995).
D. Caruana, Plasma Phys. Control. Fusion 52, 124045 (2010).
L. Wang, Z. Luo, Z. Xia, B. Liu, and X. Deng, Sci. China: Technol. Sci. 55, 2225 (2012).
D. Knight, J. Propul. Power 24, 1153 (2008).
D. D. Knight, Energy Deposition for High-speed Flow Control (Cambridge University Press, Cambridge, 2019).
N. Zouzou, E. Moreau, and G. Touchard, J. Electrost. 64, 537 (2006).
F. O. Thomas, T. C. Corke, M. Iqbal, A. Kozlov, and D. Schatzman, AIAA J. 47, 2169 (2009).
T. C. Corke, C. L. Enloe, and S. P. Wilkinson, Annu. Rev. Fluid Mech. 42, 505 (2010).
T. C. Corke, Dielectric Barrier Discharge Plasma Actuators (Lecture Series Notes for Von Karman Institute Lectures) (Von Karman Institute for Fluid Dynamics, Sint-Genesius-Rode, 2011).
T. C. Corke, M. L. Post, and D. M. Orlov, Exp. Fluids 46, 1 (2009).
A. Russell, H. Zare-Behtash, and K. Kontis, J. Electrost. 80, 34 (2016).
I. V. Adamovich, S. B. Leonov, K. Frederickson, J. G. Zheng, Y. D. Cui, and B. C. Khoo, in Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, 2017, Paper AIAA 2017-1339.
M. Samimy, N. Webb, and A. Esfahani, J. Phys. D: Appl. Phys. 52, 354002 (2019).
S. B. Leonov, V. Petrishchev, and I. V. Adamovich, J. Phys. D: Appl. Phys. 47, 465201 (2014).
S. B. Leonov, I. V. Adamovich, and V. R. Soloviev, Plasma Sources Sci. Technol. 25, 063001 (2016).
A. Starikovskiy and N. Aleksandrov, in Aeronautics and Astronautics, Ed. by M. Mulder (IntechOpen, Rijeka, 2011), Ch. 3.
A. Starikovskiy, in Encyclopedia of Plasma Technology, Ed. by J. L. Shohet (CRC, Boca Raton, FL, 2016).
V. Yu. Baranov, V. M. Borisov, and Yu. Yu. Stepanov, Electric-Discharge Noble Gas Halide Excimer Lasers (Energoatomizdat, Moscow, 1988) [in Russian].
S. M. Starikovskaia and A. Yu. Starikovskiy, in Runaway Electrons Preionized Diffuse Discharges, Ed. by V. F. Tarasenko (Nova Science, New York, 2014), p. 373.
A. Yu. Starikovskii, A. A. Nikipelov, M. M. Nudnova, and D. V. Roupassov, Plasma Sources Sci. Technol. 18, 034015 (2009).
D. V. Roupassov, A. A. Nikipelov, M. M. Nudnova, and A. Yu. Starikovskii, AIAA J. 47, 168 (2009).
N. L. Aleksandrov, A. A. Kirpichnikov, S. V. Kindusheva, I. N. Kosarev, and A. Yu. Starikovskiy, in Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2007, Paper AIAA 2007-997.
D. V. Roupassov and A. Yu. Starikovskiy, IEEE Trans. Plasma Sci. 36, 1312 (2008).
N. B. Anikin, N. A. Zavialova, S. M. Starikovskaia, and A. Y. Starikovskiy, IEEE Trans. Plasma Sci. 36, 902 (2008).
A. Starikovskiy, M. Post, N. Tkach, and R. B. Miles, in Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, 2014, Paper AIAA 2014-0144.
A. Starikovskiy and R. B. Miles, in Proceedings of the 48th AIAA Plasmadynamics and Lasers Conference, Denver, CO, 2017, Paper AIAA 2017-4159.
A. Starikovskiy and R. B. Miles, in Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, 2013, Paper AIAA 2013-754.
A. Starikovskiy, K. Meehan, J. Williams, and R. B. Miles, in Proceedings of the 48th AIAA Plasmadynamics and Lasers Conference, Denver, CO, 2017, Paper AIAA 2017-3344.
K. Meehan, J. Williams, R. B. Miles, and A. Starikovskiy, in Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, 2017, Paper AIAA 2017-1110.
Yu. P. Raizer, Gas Discharge Physics (Nauka, Moscow, 1992; Springer, Berlin, 1997).
E. M. Bazelyan and Yu. P. Raizer, Spark Discharge (MFTI, Moscow, 1997; CRC, Boca Raton, 1998).
M. M. Nudnova, N. L. Aleksandrov, and A. Yu. Starikovskii, Plasma Phys. Rep. 36, 90 (2010).
I. N. Kosarev, V. I. Khorunzhenko, E. I. Mintoussov, P. N. Sagulenko, N. A. Popov, and S. M. Starikovskaia, Plasma Sources Sci. Technol. 21, 045012 (2012).
S. A. Stepanyan, V. R. Soloviev, and S. M. Stari-kovskaia, J. Phys. D: Appl. Phys. 47, 485201 (2014).
S. B. Leonov, I. V. Adamovich, and V. R. Soloviev, Plasma Sources Sci. Technol. 25, 063001 (2016).
M. Simeni Simeni, B. M. Goldberg, C. Zhang, K. Frederickson, W. R. Lempert, and I. V. Adamovich, J. Phys. D: Appl. Phys. 50, 184002 (2017).
M. Simeni Simeni, Y. Tang, K. Frederickson, and I. V. Adamovich, Plasma Sources Sci. Technol. 27, 104001 (2018).
B. Huang, C. Zhang, I. Adamovich, Yu. Akishev, and T. Shao, Plasma Sources Sci. Technol. 29, 044001 (2020).
K. Meehan, A. Starikovskiy, and R. B. Miles, in Proceedings of the 58th AIAA Science and Technical Forum and Exposition, Orlando, FL, 2020, Paper AIAA-2020-1747.
C. Zhang, B. Huang, Z. Luo, X. Che, P. Yan, and T. Shao, Plasma Sources Sci. Technol. 28, 064001 (2019).
A. Yu. Starikovskiy and S. Pancheshnyi, in Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, 2013, Paper AIAA 2013-902.
A. Starikovskiy, S. Gordon, M. Post, and R. Miles, in Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, 2014, Paper AIAA 2014-0329.
S. E. Gordon, A. Starikovskiy, and R. B. Miles, in Proceedings of the 44th AIAA Plasmadynamics and Lasers Conference, San Diego, CA, 2013, Paper AIAA 2013-2492.
M. V. Sokolova, V. V. Voevodin, Ju. I. Malakhov, N. L. Aleksandrov, E. M. Anokhin, and V. R. Soloviev, J. Phys. D: Appl. Phys. 52, 324001 (2019).
N. Benard, N. Zouzou, A. Claverie, J. Sotton, and E. Moreau, J. Appl. Phys. 111, 033303 (2012).
S. A. Stepanyan, A. Y. Starikovskiy, N. A. Popov, and S. M. Starikovskaia, Plasma Sources Sci. Technol. 23, 045003 (2014).
A. Shcherbanev, S. A. Stepanyan, S. M. Starikovskaia, A. Yu. Khomenko, and N. A. Popov, Plasma Sources Sci. Technol. 26, 02LT01 (2017).
S. A. Shcherbanev, Ch. Ding, S. M. Starikovskaia, and N. A. Popov, Plasma Sources Sci. Technol. 28, 065013 (2019).
A. A. Ponomarev and N. L. Aleksandrov, J. Phys. D: Appl. Phys. 53, 055203 (2020).
Y. Zhu, S. Shcherbanev, B. Baron, and S. Starikov-skaia, Plasma Sources Sci. Technol. 26, 125004 (2017).
V. R. Soloviev, E. M. Anokhin, and N. L. Aleksandrov, Plasma Sources Sci. Technol. 29, 035006 (2020).
V. R. Soloviev and V. M. Krivtsov, Plasma Sources Sci. Technol. 27, 114001 (2018).
H. Nishida, T. Nonomura, and T. Abe, J. Appl. Phys. 115, 133301 (2014).
V. R. Soloviev, Plasma Phys. Rep. 45, 264 (2019).
S. V. Pancheshnyi, D. A. Lacoste, A. Bourdon, and C. O. Laux, IEEE Trans. Plasma Sci. 34, 2478 (2006).
C. K. Kruger, C. O. Laux, L. Yu, D. Packan, and L. Pierrot, Pure Appl. Chem. 74, 337 (2002).
D. Z. Pai, G. D. Stancu, D. A. Lacoste, and C. O. Laux, Plasma Sources Sci. Technol. 18, 045030 (2009).
D. Z. Pai, D. A. Lacoste, and C. O. Laux, Plasma Sources Sci. Technol. 19, 065015 (2010).
D. Z. Pai, D. A. Lacoste, and C. O. Laux, J. Appl. Phys. 107, 093303 (2010).
D. L. Rusterholtz, D. A. Lacoste, G. D. Stancu, D. Z. Pai, and C. O. Laux, J. Phys. D: Appl. Phys. 46, 464010 (2013).
D. A. Xu, M. N. Shneider, D. A. Lacoste, and C. O. Laux, J. Phys. D: Appl. Phys. 47, 235202 (2014).
G. V. Naidis, J. Phys. D: Appl. Phys. 41, 234017 (2008).
M. Samimy, I. Adamovich, B. Webb, J. Kastner, J. Hileman, S. Keshav, and P. Palm, Exp. Fluids 37, 577 (2004).
Y. Kolesnichenko, V. Brovkin, O. Azarova, V. Grudnitsky, V. Lashkov, and I. Mashek, in Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2003, Paper AIAA 2003-0361.
K. Kourtzanidis, F. Rogier, and J.-P. Boeuf, J. Appl. Phys. 118, 103301 (2015).
S. C. Schaub, J. S. Hummelt, W. C. Guss, M. A. Shapiro, and R. J. Temkin, Phys. Plasmas 23, 083512 (2016).
Yu. P. Raizer, Laser-Induced Discharge Phenomena (Nauka, Moscow, 1974; Consultants Bureau, New York, 1977).
C. G. Morgan, Rep. Prog. Phys. 38, 621 (1975).
Laser-Induced Plasmas and Applications, Ed. by L. J. Radziemski and D. A. Cremers (Marcel Dekker, New York, 1989).
R. Kandala and G. V. Candler, in Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2005, Paper AIAA 2005-205.
M. Thiyagarajan and J. E. Scharer, IEEE Trans. Plasma Sci. 36, 2512 (2008).
M. Thiyagarajan and S. Thompson, J. Appl. Phys. 111, 073302 (2012).
A. P. Yalin, C. Dumitrache, N. Wilvert, S. Joshi, and M. N. Shneider, Phys. Plasmas 21, 103511 (2014).
C. Dumitrache, R. VanOsdol, C. M. Limbach, and A. P. Yalin, Sci. Rep. 7, 10239 (2017).
N. Glumac, G. Elliott, and M. Boguszko, in Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2005, Paper AIAA 2005-204.
C. Dumitrache, C. M. Limbach, and A. P. Yalin, Phys. Plasmas 23, 093515 (2016).
R. Mahamud, A. A. Tropina, R. B. Miles, and M. N. Shneider, Phys. Fluids 30, 106104 (2018).
A. Couairon and A. Mysyrowicz, in Springer Series in Chemical Physics, Ed. by A. W. Castelman, Jr., J. P. Toennies, and W. Zinth, Vol. 84: Progress in Ultrafast Intense Laser Science I, Ed. by K. Yamanouchi, S. L. Chin, P. Agostini, and G. Ferrante (Springer-Verlag, Berlin, Heidelberg, 2006), p. 235.
P.-Q. Elias, N. Severac, J.-M. Luyssen, J.-P. Tobeli, F. Lambert, R. Bur, A. Houard, A. Yves-Bernard, A. Sylvain, A. Mysyrowicz, and I. Doudet, in Proceedings of the 54th AIAA/SEA/ASEE Joint Propulsion Conference (AIAA Propulsion and Energy Forum), Cincinnati, OH, 2018, Paper AIAA 2018-4896.
N. L. Aleksandrov, S. B. Bodrov, M. V. Tsarev, A. A. Murzanev, Yu. A. Sergeev, Yu. A. Malkov, and A. N. Stepanov, Phys. Rev. E 94, 013204 (2016).
N. L. Aleksandrov, S. V. Kindusheva, A. A. Kirpichnikov, I. N. Kosarev, S. M. Starikovskaia, and A. Yu. Starikovskiy, J. Phys. D: Appl. Phys. 40, 4493 (2007).
N. L. Aleksandrov, S. V. Kindusheva, I. N. Kosarev, and A. Yu. Starikovskiy, J. Phys. D: Appl. Phys. 41, 215207 (2008).
V. L. Bychkov and A. V. Eletskii, in Plasma Chemistry, Ed. by B. M Smirnov (Energoatomizdat, Moscow, 1985), Vol. 12, p. 9 [in Russian].
N. L. Aleksandrov, E. M. Anokhin, S. V. Kindysheva, A. A. Kirpichnikov, I. N. Kosarev, M. M. Nudnova, S. M. Starikovskaia, and A. Yu. Starikovskii, Plasma Phys. Rep. 38, 179 (2012).
N. L. Aleksandrov, E. M. Anokhin, S. V. Kindysheva, A. A. Kirpichnikov, I. N. Kosarev, M. M. Nudnova, S. M. Starikovskaia, and A. Yu. Starikovskiy, J. Phys. D: Appl. Phys. 45, 255202 (2012).
M. J. McEwan and L. F. Phillips, Chemistry of the Atmosphere (Halsted, New York, 1975).
I. A. Kossyi, A. Yu. Kostinsky, A. A. Matveyev, and V. P. Silakov, Plasma Sources Sci. Technol. 1, 207 (1992).
M. Capitelli, C. M. Ferreira, B. F. Gordiets, and A. I. Osipov, Plasma Kinetics in Atmospheric Gases (Springer-Verlag, Berlin, 2000).
Yu. S. Akishev, A. A. Deryugin, V. B. Karal’nik, I. V. Kochetov, A. P. Napartovich, and N. I. Trushkin, Plasma Phys. Rep. 20, 511 (1994).
L. W. Sieck, J. T. Herron, and D. S. Green, Plasma Chem. Plasma Process. 20, 235 (2000).
I. A. Soloshenko, V. V. Tsiolko, S. S. Pogulay, A. G. Kalyuzhnaya, V. Yu. Bazhenov, and A. I. Shchedrin, Plasma Sources Sci. Technol. 18, 045019 (2009).
A. V. Filippov, I. N. Derbenev, N. A. Dyatko, S. A. Kurkin, G. B. Lopantseva, A. F. Pal’, and A. N. Starostin, J. Exp. Theor. Phys. 125, 246 (2017).
A. I. Florescu-Mitchell and J. B. A. Mitchell, Phys. Rep. 430, 277 (2006).
M. T. Leu, M. A. Biondi, and R. Johnsen, Phys. Rev. A: 7, 292 (1973).
C.-M. Huang, M. Whitaker, M. A. Biondi, and R. Johnsen, Phys. Rev. A: 18, 64 (1978).
R. Johnsen, J. Chem. Phys. 98, 5390 (1993).
M. A. Popov, I. V. Kochetov, A. Yu. Starikovskiy, and N. L. Aleksandrov, J. Phys. D: Appl. Phys. 51, 264003 (2018).
M. B. Någård, J. B. C. Pettersson, A. M. Derkatch, A. Al Khalili, A. Neau, S. Rosén, M. Larsson, J. Semaniak, H. Danared, A. Källberg, and F. Österdahl, J. Chem. Phys. 117, 5264 (2002).
J. Öjekull, P. U. Andersson, M. B. Någård, J. B. C. Pettersson, N. Marković, A. M. Derkatch, A. Neau, A. Al Khalili, S. Rosén, M. Larsson, J. Semaniak, H. Danared, A. Källberg, F. Österdahl, and M. af Ugglas, J. Chem. Phys. 127, 194301 (2007).
J. Öjekull, P. U. Andersson, J. B. C. Pettersson, N. Marković, R. D. Thomas, A. Al Khalili, A. Ehlerding, F. Österdahl, M. af Ugglas, M. Larsson, H. Danared, and A. Källberg, J. Chem. Phys. 128, 044311 (2007).
R. Johnsen, J. Phys.: Conf. Ser. 204, 012006 (2010).
B. M. Smirnov, Ions and Excited Atoms in Plasma (Atomizdat, Moscow, 1974) [in Russian].
L. M. Biberman, V. S. Vorob’ev, and I. T. Yakubov, Kinetics of Nonequilibrium Low-Temperature Plasmas (Nauka, Moscow, 1982; Consultants Bureau, New York, 1987).
E. M. Anokhin, M. A. Popov, I. V. Kochetov, N. L. Aleksandrov, and A. Yu. Starikovskii, Plasma Phys. Rep. 42, 59 (2016).
T. Kotrík, P. Dohnal, Š. Roučka, P. Jusko, R. Plašil, J. Glosík, and R. Johnsen, Phys. Rev. A: 83, 032720 (2011).
N. A. Dyatko, Yu. Z. Ionikh, N. B. Kolokolov, A. V. Meshchanov, and A. P. Napartovich, IEEE Trans. Plasma Sci. 31, 553 (2003).
N. A. Dyatko, I. V. Kochetov, and A. P. Napartovich, Plasma Phys. Rep. 28, 965 (2002).
N. L. Aleksandrov and E. M. Bazelyan, Plasma Sources Sci. Technol. 8, 285 (1999).
T. Huiskamp, A. J. M. Pemen, W. F. L. M. Hoeben, F. J. C. M. Beckers, and E. J. M. van Heesch, J. Phys. D: Appl. Phys. 46, 165202 (2013).
R. Ono and Y. Ishikawa, J. Phys. D: Appl. Phys. 51, 185204 (2018).
A. Komuro, S. Matsuyuki, and A. Ando, Plasma Sources Sci. Technol. 27, 105001 (2018).
A. Lo, A. Cessou, P. Boubert, and P. Vervisch, J. Phys. D: Appl. Phys. 47, 115201 (2014).
A. Lo, A. Cessou, and P. Vervisch, J. Phys. D: Appl. Phys. 47, 115202 (2014).
A. V. Klochko, S. M. Starikovskaia, Z. Xiong, and M. J. Kushner, J. Phys. D: Appl. Phys. 47, 365202 (2014).
N. A. Popov, Plasma Sources Sci. Technol. 25, 044003 (2016).
D. L. Rusterholtz, D. Z. Pai, G. D. Stancu, D. A. Lacoste, and C. O. Laux, in Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, 2012, Paper AIAA 2012-0509.
N. Aleksahdrov, E. Anokhin, S. Kindusheva, A. Kirpichnikov, I. Kosarev, M. Nudnova, S. Starikovskaia, and A. Starikovskiy, in Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, 2012, Paper AIAA 2012-511.
N. Aleksahdrov, S. Kindusheva, and A. Starikovskiy, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-1330.
N. Aleksandrov, S. Kindusheva, M. Nudnova, and A. Starikovskiy, in Proceedings of the 48th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2010, Paper AIAA 2010-0465.
N. L. Aleksandrov, A. A. Kirpichnikov, S. V. Kindusheva, I. N. Kosarev, and A. Yu. Starikovskiy, in Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2007, Paper AIAA 2007-0997.
N. L. Aleksandrov, S. V. Kindusheva, I. N. Kosarev, and A. Yu. Starikovskiy, in Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2009, Paper AIAA 2009-1048.
M. Nudnova, S. Kindusheva, N. Aleksahdrov, and A. Starikovskiy, in Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, 2012, Paper AIAA 2012-510.
A. S. Zarin, A. A. Kuzovnikov, and V. M. Shibkov, Freely Localized Microwave Discharge in Air (Neft’ i Gaz, Moscow, 1996) [in Russian].
N. A. Popov, Plasma Phys. Rep. 27, 886 (2001).
I. A. Znamenskaya, D. F. Latfullin, A. E. Lutskii, I. V. Mursenkova, and N. N. Sysoev, Tech. Phys. 52, 546 (2007).
T. V. Bazhenova, I. A. Znamenskaya, A. E. Lutskii, and I. V. Mursenkova, High Temp. 45, 523 (2007).
I. A. Znamenskaya, D. F. Latfullin, A. E. Lutskii, and I. V. Mursenkova, Tech. Phys. Lett. 36, 795 (2010).
E. M. Anokhin, S. M. Starikovskaia, and A. Yu. Starikovskiy, in Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2004, Paper AIAA 2004-674.
N. L. Aleksandrov, S. V. Kindusheva, M. M. Nudnova, and A. Yu. Starikovskiy, J. Phys. D: Appl. Phys. 43, 255201 (2010).
M. M. Nudnova, S. V. Kindysheva, N. L. Aleksandrov, and A. Yu. Starikovskiy, Philos. Trans. R. Soc., A 373, 20140330 (2015).
E. I. Mintoussov, J. Pendleton, F. G. Gerbault, N. A. Popov, and S. M. Starikovskaia, J. Phys. D: Appl. Phys. 44, 285202 (2011).
N. A. Popov, J. Phys. D: Appl. Phys. 44, 285201 (2011).
A. Flitti and S. Pancheshnyi, Eur. Phys. J.: Appl. Phys. 45, 21001 (2009).
Y. Zhu and S. Starikovskaia, Plasma Sources Sci. Technol. 27, 124007 (2018).
K. Oswatitsch, Report No. 90 (German Aerospace Center, Cologne, 1959).
M. N. Shneider, S. O. Macheret, S. H. Zaidi, I. G. Girgis, and R. B. Miles, J. Propul. Power 24, 900 (2008).
R. Meyer, P. Palm, E. Ploenjes, J. W. Rich, and I. V. Adamovich, AIAA J. 41, 465 (2003).
R. B. Miles, S. O. Macheret, L. Martinelli, R. Murray, M. Shneider, Yu. Z. Ionikh, J. Kline, and J. Fox, in Proceedings of the 32nd AIAA Plasmadynamics and Lasers Conference and 4th Weakly Ionized Gases Workshop, Anaheim, CA, 2001, Paper AIAA 2001-3062.
S. O. Macheret, Y. Z. Ionikh, N. V. Chernysheva, A. P. Yalin, L. Martinelli, and R. B. Miles, Phys. Fluids 13, 2693 (2001).
V. I. Khorunzhenko, D. V. Roupassov, and A. Yu. Starikovskiy, in Proceedings of the 38th AIAA/ASME/ SAE/ASEE Joint Propulsion Conference and Exhibit, Indianapolis, IN, 2002, Paper AIAA 2002-2497.
V. I. Khorunzhenko, D. V. Roupassov, and A. Yu. Starikovskiy, in Proceedings of the 11th AIAA/AAAF International Conference Space Planes and Hypersonic Systems and Technologies, Orleans, 2002, Paper AIAA 2002-5186.
V. I. Khorunzhenko, D. V. Roupassov, S. M. Stari-kovskaia, and A. Yu. Starikovskiy, in Proceedings of the 39th AIAA/ ASME/ SAE/ ASEE Joint Propulsion Conference and Exhibit, Huntsville, AL, 2003, Paper AIAA 2003-5048.
P.-Q. Elias, B. Chanetz, S. Larigaldie, and D. Packan, AIAA J. 45, 2237 (2007).
M. Nishihara, K. Takashima, J. W. Rich, and I. V. Adamovich, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-1144.
N. Bisek, J. Poggie, M. Nishihara, and I. V. Adamovich, in Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, 2012, Paper AIAA 2012-0186.
V. I. Artem’ev, V. I. Bergelson, I. V. Nemchinov, T. I. Orlova, V. A. Rybakov, V. A. Smirnov, and V. M. Khazins, Mat. Model. 1(8), 1 (1989).
H. Mark, J. Aeronaut. Sci. 24, 304 (1957).
W. Griffiths, J. Aeronaut. Sci. 23, 19 (1956).
A. M. Lashin and A. Yu. Starikovskiy, Tech. Phys. 40, 754 (1995).
A. M. Lashin and A. Yu. Starikovskiy, Teplofiz. Vys. Temp. 33, 1 (1995).
V. I. Artem’ev, V. I. Bergel’son, I. V. Nemchinov, T. I. Orlova, V. A. Smirnov, and V. M. Khazins, Fluid Dyn. 24, 779 (1989).
D. F. Opaits, D. V. Roupassov, S. M. Starikovskaia, and A. Yu. Starikovskiy, in Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2004, Paper AIAA 2004-1023.
O. Azarova, D. Knight, and Y. Kolesnichenko, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-1026.
R. Adelgren, G. Elliott, D. Knight, A. Zheltovodov, and T. Beutner, in Proceedings of the 39th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2001, Paper AIAA 2001-0885.
Yu. F. Kolesnichenko, V. G. Brovkin, D. V. Khmara, V. A. Lashkov, I. Ch. Mashek, and M. I. Ryvkin, in Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2003, Paper AIAA 2003-362.
J. S. Shang, AIAA J. 40, 1178 (2002).
E. Erdem, L. Yang, and K. Kontis, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-1027.
V. G. Brovkin, S. A. Afanas’ev, D. V. Khmara, and Yu. F. Kolesnichenko, in Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2006, Paper AIAA 2006-1459.
Yu. F. Kolesnichenko, V. G. Brovkin, D. V. Khmara, I. Ch. Mashek, V. A. Lashkov, and M. I. Ryvkin, in Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2006, Paper AIAA 2006-0792.
J. B. Michael, A. Dogariu, M. N. Shneider, and R. B. Miles, J. Appl. Phys. 108, 093308 (2010).
G. Emanuel, M. C. Cline, and K. H. Witte, in Proceedings of the 13th AIAA Fluid and Plasma Dynamics Conference, Snowmass, CO, 1980, Paper AIAA 80-1381.
A. Alberti, A. Munaf, C. Pantano, and M. Panesi, in Proceedings of the AIAA Aiation 2019 Forum, Dallas, TX, 2019, Paper AIAA 2019-2867.
P. Yu. Georgievskii and V. A. Levin, Mechanics: Modern Problems (Izd.-vo MGU, Moscow, 1987), p. 93 [in Russian].
A. Starikovskiy, C. Limbach, and R. B. Miles, in Proceedings of the 47th AIAA Plasmadynamics and Lasers Conference, Washington, D.C., 2016, Paper AIAA 2016-4308.
A. Starikovskiy, C. Limbach, and R. B. Miles, in Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, 2016, Paper AIAA 2016-0459.
A. P. Khamseh, R. M. Kiriakos, and E. P. DeMauro, in Proceedings of the 58th AIAA Science and Technical Forum and Exposition, Orlando, FL, 2020, Paper AIAA 2020-1059.
N. Kianvashrad and D. Knight, J. Phys. D: Appl. Phys. 52, 494005 (2019).
J.-H. Kim, M. Nishihara, S. Keshav, I. V. Adamovich, M. Samimy, S. V. Gorbatov, and F. V. Pliavaka, in Proceedings of the 40th Plasmadynamics and Lasers Conference, San Antonio, TX, 2009, Paper AIAA 2009-4071.
M. Samimy, M. Kearney-Fischer, J.-H. Kim, and A. Sinha, J. Propul. Power 28, 269 (2012).
D. R. Gonzalez, D. V. Gaitonde, and M. J. Lewis, in Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, 2015, Paper AIAA 2015-1037.
R. Ely and J. Little, in Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, 2013, Paper AIAA 2013-1012.
R. Ely and J. Little, in Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, 2013, Paper AIAA 2013-2753.
R. Lehmann, D. Akins, and J. Little, AIAA J. 54, 637 (2016).
A. Singh and J. Little, J. Phys. D: Appl. Phys. 53, 164004 (2020).
M. Samimy, J.-H. Kim, J. Kastner, I. Adamovich, and Y. Utkin, J. Fluid Mech. 578, 305 (2007).
C. S. Kalra, S. Zaidi, and R. B. Miles, in Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2008, Paper AIAA 2008-1092.
C. S. Kalra, M. N. Shneider, and R. B. Miles, in Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2008, Paper AIAA 2008-1095.
N. Webb, C. Clifford, and M. Samimy, in Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, HI, 2011, Paper AIAA 2011-3426.
N. Webb, C. Clifford, and M. Samimy, in Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, 2013, Paper AIAA 2013-0402.
K. Kinefuchi, A. Starikovskiy, and R. Miles, in Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, 2016, Paper AIAA 2016-5070.
K. Kinefuchi, A. Starikovskiy, and R. Miles, J. Propul. Power 34, 909 (2018).
K. Kinefuchi, A. Starikovskiy, and R. Miles, Phys. Fluids 30, 106105 (2018).
S. Grundmann and C. Tropea, Exp. Fluids 42, 653 (2007).
F. O. Thomas, T. C. Corke, A. Duong, S. Midya, and K. Yates, J. Phys. D: Appl. Phys. 52, 434001 (2019).
A. Duong, T. C. Corke, and F. O. Thomas, in Proceedings of the 58th AIAA Science and Technical Forum and Exposition, Orlando, FL, 2020, Paper AIAA 2020-0098.
H. Velkoff and J. Ketchman, AIAA J. 16, 1381 (1968).
A. Yabe, Y. Mori, and K. Hijikata, AIAA J. 16, 340 (1978).
L. Léger, E. Moreau, and G. Touchard, in Proceedings of the IEEE-IAS World Conference on Industrial Applications of Electrical Energy. Chicago, IL, 2001.
L. Léger, E. Moreau, G. Artana, and G. Touchard, J. Electrost. 51−52, 300 (2001).
M. Forte, J. Jolibois, E. Moreau, G. Touchard, and M. Cazalens, in Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, 2006, Paper AIAA 2006-2863.
K. Allegraud, O. Guaitella, and A. Rousseau, J. Phys. D: Appl. Phys. 40, 7698 (2007).
J. W. Gregory, C. L. Enloe, G. I. Font, and T. E. McLaughlin, in Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2007, Paper AIAA 2007-185.
T. Abe, Y. Takizawa, S. Sato, and N. Kimura, in Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2007, Paper AIAA 2007-187.
A. V. Likhanskii, M. N. Shneider, D. F. Opaits, R. B. Miles, and S. O. Macheret, in Proceedings of the 48th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2010, Paper AIAA 2010-470.
D. F. Opaits, D. V. Roupassov, S. M. Starikovskaia, A. Yu. Starikovskiy, I. N. Zavialov, and S. G. Saddoughi, in Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2005, Paper AIAA 2005-1180.
D. V. Roupassov, I. N. Zavyalov, A. Yu. Starikovskiy, and S. G. Saddoughi, in Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2006, Paper AIAA 2006-373.
M. P. Patel, T. T. Ng, S. Vasudevan, T. C. Corke, M. L. Post, T. E. McLaughlin, and C. F. Suchomel, in Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2007, Paper AIAA 2007-635.
A. A. Sidorenko, B. Yu. Zanin, B. V. Postnikov, A. D. Budovsky, A. Yu. Starikovskiy, D. V. Roupassov, I. N. Zavialov, N. D. Malmuth, P. Smereczniak, and J. S. Silkey, in Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2007, Paper AIAA 2007-941.
A. A. Sidorenko, A. D. Budovsky, A. V. Pushkarev, and A. A. Maslov, in Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2008, Paper AIAA 2008-373.
D. V. Roupassov, I. N. Zavyalov, A. Yu. Starikovskiy, and S. G. Saddoughi, in Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cincinnati, OH, 2007, Paper AIAA 2007-4530.
D. Roupassov, M. Nudnova, A. Nikipelov, and A. Starikovskiy, in Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2008, Paper AIAA 2008-1367.
A. Nikipelov, M. Nudnova, D. Roupassov, and A. Starikovskiy, in Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2009, Paper AIAA 2009-695.
G. Correale, I. B. Popov, A. E. Rakitin, A. Yu. Starikovskiy, S. J. Hulshoff, and L. L. M. Veldhuis, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-1079.
G. Correale, F. Avallone, and A. Y. Starikovskiy, J. Phys. D: Appl. Phys. 49, 505201 (2016).
M. Rios, M. Nudnova, S. Kindusheva, N. Aleksahdrov, and A. Starikovskiy, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-1275.
M. R. Visbal and D. V. Gaitonde, in Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, 2006, Paper AIAA 2006-505.
C. Rethmel, J. Little, K. Takashima, A. Sinha, I. Adamovich, and M. Samimy, in Proceedings of the 49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, 2011, Paper AIAA 2011-0487.
T. Unfer and J. P. Boeuf, J. Phys. D: Appl. Phys. 42, 194017 (2009).
J. Little, A. Singh, T. Ashcraft, and C. Durasiewicz, Plasma Sources Sci. Technol. 28, 014002 (2019).
I. V. Adamovich, S. B. Leonov, K. Frederickson, J. G. Zheng, Y. D. Cui, and B. C. Khoo, in Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, 2017, Paper AIAA 2017-1339.
A. Bright, N. Tichenor, K. Kremeyer, and R. Wlezien, AIAA J. 56, 1472 (2018).
A. Komuro, K. Takashima, K. Suzuki, S. Kanno, T. Nonomura, T. Kaneko, A. Ando, and K. Asai, Plasma Sources Sci. Technol. 27, 104005 (2018).
M. M. Nudnova and A. Yu. Starikovskiy, in Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, 2012, Paper AIAA 2012-407.
D. V. Gaitonde, M. Sahin, K. Shaler, B. Glaz, and S. P. G. Dinavahi, in Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, 2013, Paper AIAA 2013-1118.
Z. Chen, L. Hao, B. Zhang, H. Liang, and Y. Li, in Proceedings of the 43rd Fluid Dynamics Conference, San Diego, CA, 2013, Paper AIAA 2013-2743.
A. Marino, P. Catalano, C. Marongiu, P. Peschke, C. Hollenstein, and R. Donelli, in Proceedings of the 43rd Fluid Dynamics Conference, San Diego, CA, 2013, Paper AIAA 2013-2752.
P. Peschke, S. Goekce, P. Leyland, P. Ott, and Ch. Hollenstein, in Proceedings of the 44th AIAA Plasmadynamics and Lasers Conference, San Diego, CA, 2013, Paper AIAA 2013-2885.
I. Popov, A. Nikipelov, S. Pancheshnyi, G. Correale, S. Hulshoff, L. Veldhuis, S. Zaidi, and A. Starikovskiy, in Proceedings of the 51st AIAA Aerospace Sciences Meeting, Grapevine, TX, 2013, Paper AIAA 2013-572.
A. Starikovskiy, K. Meehan, J. Williams, and R. B. Miles, in Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, 2017, Paper AIAA 2017-1342.
J. G. Zheng, Y. D. Cui, Z. J. Zhao, J. Li, and B. C. Khoo, Phys. Rev. Fluids 1, 073501 (2016).
J. G. Zheng, Y. D. Cui, Z. J. Zhao, J. Li, and B. C. Khoo, AIAA J. 56, 2200 (2018).
Y. Iwasaki, T. Nonomura, K. Nankai, K. Asai, S. Kanno, K. Suzuki, A. Komuro, A. Ando, K. Takashima, T. Kaneko, H. Yasuda, K. Hayama, T. Tsujiuchi, T. Nakajima, and K. Nakakita, Energies 13, 1376 (2020).
A. G. Isfahani, N. Webb, and M. Samimy, in Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, 2017, Paper AIAA 2017-1577.
M. Frankhouser, K. Hird, S. Naigle, J. W. Gregory, and J. P. Bons, in Proceedings of the 46th AIAA Plasmadynamics and Lasers Conference, Dallas, TX, 2015, Paper AIAA 2015-2341.
A. Starikovskiy, J. Williams, and R. B. Miles, in Proceedings of the 48th AIAA Plasmadynamics and Lasers Conference, Denver, CO, 2017, Paper AIAA 2017-3342.
A. Starikovskiy, K. Meehan, and R. B. Miles, in Proceedings of the 56th AIAA Science and Technical Forum and Exposition, Kissimmee, FL, 2018, Paper AIAA 2018-0681.
A. Starikovskiy, K. Meehan, N. Persikov, and R. B. Miles, Plasma Sources Sci. Technol. 28, 054001 (2019).
N. Whiting, D. Castañeda, N. Webb, and M. Samimy, in Proceedings of the 58th AIAA Science and Technical Forum and Exposition, Orlando, FL, 2020, Paper AIAA 2020-1568.
A. Starikovskiy, N. Persikov, and R. B. Miles, in Proceedings of the 56th AIAA Science and Technical Forum and Exposition, Kissimmee, FL, 2018, Paper AIAA 2018-0936.
C. Kolbakir, Y. Liu, H. Hu, A. Starikovskiy, and R. B. Miles, in Proceedings of the 56th AIAA Science and Technical Forum and Exposition, Kissimmee, FL, 2018, Paper AIAA 2018-0164.
Y. Liu, C. Kolbakir, A. Starikovskiy, R. B. Miles, and H. Hu, Plasma Sources Sci. Technol. 28, 014001 (2019).
Y. Zhu, Y. Wu, B. Wei, H. Xu, H. Liang, M. Jia, H. Song, and Y. Li, J. Phys. D: Appl. Phys. 53, 145205 (2020).
B. Wei, Y. Wu, H. Liang, Y. Zhu, J. Chen, G. Zhao, H. Song, M. Jia, and H. Xu, Int. J. Heat Mass Transfer 138, 163 (2019).
Funding
This study was supported by the Russian Foundation for Basic Research, project no. 19-12-50047.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated by E. Chernokozhin
Rights and permissions
Open Access. This article is distributed under the terms of the Creative Commons Attribution 4.0 International License http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Starikovskiy, A.Y., Aleksandrov, N.L. Gasdynamic Flow Control by Ultrafast Local Heating in a Strongly Nonequilibrium Pulsed Plasma. Plasma Phys. Rep. 47, 148–209 (2021). https://doi.org/10.1134/S1063780X21020069
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1063780X21020069