Skip to main content
SpringerLink
Log in

On the Solution to One Problem of Magnetostatics for a Pipe with Inner Surface Defect

  • ELECTROMAGNETIC METHODS
  • Published:
Russian Journal of Nondestructive Testing Aims and scope Submit manuscript

Abstract

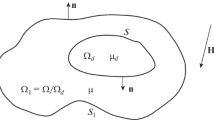
An algorithm has been developed and implemented for the numerical solution of a direct linear magnetostatics problem by calculating the resulting field of a pipe with a surface defect on its inner wall under the assumption that the perpendicular section of the pipe and the vector of intensity of the external magnetizing field remain unchanged along the pipe length axis. This has made it possible to take the two-dimensional integro-differential equation of magnetostatics as a basis. The algorithm is implemented in the FORTRAN programming language. The results are tested for reliability using problems solved exactly. Illustrative curves are constructed. The possibilities of applying the obtained calculation methodology to a class of problems that differ in some way in their formulation are indicated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.

Similar content being viewed by others

REFERENCES

  1. Zatsepin, N.N. and Shcherbinin, V.E., To the calculation of magnetostatic field of surface defects, Defektoskopiya, 1966, no. 5, pp. 50–59.

  2. Shcherbinin, V.E. and Zatsepin, N.N., On the calculation of the magnetostatic field of surface defects. II. Experimental verification of the main computational patterns, Defektoskopiya, 1966, no. 5, pp. 59–65.

  3. Krotov, L.N., Reconstruction of a media boundary based on the spatial distribution of stray magnetic fields. II. Definition and method of solving the inverse geometric problem of magnetostatics, Russ. J. Nondestr. Test., 2004, vol. 40, no. 6, pp. 385–390.

    Article  Google Scholar 

  4. Krotov, L.N., Reconstruction of a media Interface from the spatial distribution of a magnetic stray field: I. Analysis of the properties of the solution of the auxiliary direct problem (linear approximation), Russ. J. Nondestr. Test., 2004, vol. 40, no. 2, pp. 130–134.

    Article  Google Scholar 

  5. Dyakin, V.V., Kudryashova, O.V., and Rayevskii, V.Ya., Stray field of plate with a surface defect in a homogeneous external field, Russ. J. Nondestr. Test., 2018, no. 12, pp. 840–848.

  6. Khizhnyak, N.A., Integral’nye uravneniya makroskopicheskoi elektrodinamiki (Integral Equations of Macroscopic Electrodynamics), Kiev: Naukova Dumka, 1986.

  7. Dyakin, V.V., Matematicheskie osnovi klassicheskoi magnitostatiki (Mathematical Foundations of Classical Magnetostatics), Yekaterinburg: Ural Branch, Russ. Acad. Sci., 2016.

  8. Mikhlin, S.G., Kurs matematicheskoi fiziki (Course of Mathematical Physics), Moscow: Nauka, 1968.

  9. Gradshtein, I.S. and Ryzhik, I.M., Tablitsy integralov, summ, ryadov i proizvedenii (Tables of Integrals, Sums, Series, and Products), Moscow: GIFML, 1962.

  10. Forsythe, J., Malcolm, M., and Mouler, K., Computer Methods for Mathematical Computations, Hoboken: Prentice-Hall, 1977.

Download references

ACKNOWLEDGEMENTS

The authors thank A.V. Gapontsev for his help in setting the problem and interest in the results of its solution.

Funding

This work was carried out within the framework of the state assignment on topic “Quantum,” project no. AAAA-А18-118020190095-4.

Author information

Authors and Affiliations

  1. Mikheev Institute of Metal Physics, Ural Branch, Russian Academy of Sciences, 620108, Yekaterinburg, Russia

    V. V. Dyakin, O. V. Kudryashova & V. Ya. Rayevskii

Authors
  1. V. V. Dyakin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. V. Kudryashova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. Ya. Rayevskii
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. V. Kudryashova.

Ethics declarations

The authors declare that they have no conflicts of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dyakin, V.V., Kudryashova, O.V. & Rayevskii, V.Y. On the Solution to One Problem of Magnetostatics for a Pipe with Inner Surface Defect. Russ J Nondestruct Test 59, 204–214 (2023). https://doi.org/10.1134/S1061830923700274

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1061830923700274

Keywords:

Search

Navigation