Skip to main content
SpringerLink
Log in

Analysis of Guided Waves Dispersion and Acoustoelastic Effect in Stressed Waveguides by Eigenfrequency Method and Experimental Study

  • ACOUSTIC METHODS
  • Published:
Russian Journal of Nondestructive Testing Aims and scope Submit manuscript

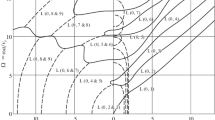
Abstract

On the basis of the effect of initial stress and acoustoelastic coefficients on the dispersion behavior of guided waves in stressed waveguides. a finite element method is presented to analyze the wave propagation in prestressed waveguides. The approach was based on the acoustoelastic theory to solve the eigenfrequency of prestressed waveguides, where wavenumbers and modes are distinguished by modal shape, and the solutions of the phase velocity and the group velocity were determined. The algorithm was applied to analyze the dispersion and acoustoelastic coefficients of a prestressed plate and an axisymmetric bar model. Obtained results were consistent with previous research, proving that the approach is useful for the analysis of dispersion and acoustoelastic effect in prestressed waveguides. The acoustoelastic effect of the longitudinal mode guided wave in the rod was experimentally studied according to on the method of eigenfrequency analysis. The results show that the trend of the experimental results is in good agreement with that of the eigenfrequency method. The detection frequency of L(0.1) mode is around 72 kHz, the error of L(0.2) mode is small in the range of 240–280 kHz, which is more suitable for acoustoelastic stress detection.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.

Similar content being viewed by others

REFERENCES

  1. Crecraft, D.I., Ultrasonic measurement of stress, Ultrasonics, 1968, no. 2, p. 117.

    Article  Google Scholar 

  2. Yu, F., Gupta, N., and Hoy, J., Nonintrusive pressure measurement based on ultrasonic waves, Insight, 2005, vol. 47, no. 5, pp. 285–288.

    Article  Google Scholar 

  3. Tanala, E., Bourse, G., Fremiot, M., et al., Determination of near surface residual stresses on welded joints using ultrasonic methods, NDT & E Int., 1995, vol. 28, no. 2, pp. 83–88.

    Article  CAS  Google Scholar 

  4. Hirao, M., Ogi, H., and Yasui, H., Contactless measurement of bolt axial stress using a shear wave electromagnetic acoustic transducer, NDT & E Int., 2001, vol. 34, no. 3, pp. 179–183.

    Article  CAS  Google Scholar 

  5. Chen, H.L.R., He, Y., and Ganga Rao, Measurement of prestress force in the rods of stressed timber bridges using stress waves, Mater. Eval., 1998, vol. 56, no. 8, pp. 977–981.

    CAS  Google Scholar 

  6. Kwun, H., Bartels, K.A., and Hanley, J.J., Effect of tensile loading on the properties of elastic wave in a strand, J. Acoust. Soc. Am., 1998, vol. 103, no. 6, pp. 3370–3375.

    Article  Google Scholar 

  7. Ozevin, D., Numerical and experimental demonstration of shear stress measurement at thick steel plates using acoustoelasticity, in Proc. SPIE Int. Soc. Opt. Eng., 2015, 9437.

  8. Ning, P. and Bond, L.J., Higher order acoustoelastic Lamb wave propagation in stressed plates, Acoust. Soc. Am., 2016, vol. 140, no. 5, pp. 3834–3843.

    Article  Google Scholar 

  9. Ellwood, R., Stratoudaki, T., Sharples, S.D., et al., Imaging textural variation in the acoustoelastic coefficient of aluminum using surface acoustic waves, Acoust. Soc. Am., 2015, vol. 138, 2811.

    Article  CAS  Google Scholar 

  10. Kwaśniewki, J., Dominikn, I., Lalik, K., and Holewa, K., Influence of acoustoelastic coefficient on wave time of flight in stress measurement in piezoelectric self excited system, Mech. Syst. Signal Process., 2016, vol. 78, pp. 143–155.

    Article  Google Scholar 

  11. Abbasi, Z. and Ozevin, D., Acoustoelastic coefficients in thick steel plates under normal and shear stresses, Exp. Mech., 2016, vol. 56, no. 9, pp. 1–17.

    Article  Google Scholar 

  12. Chen, F. and Wilcox, P.D., The effect of load on guided wave propagation, Ultrasonics, 2007, vol. 47, pp. 111–122.

    Article  Google Scholar 

  13. di Scalea, F.L., Rizzo, P., and Seible, F., Stress measurement and defect detection in steel strands by guided stress waves, J. Mater. Civ. Eng., 2003, vol. 15, no. 3, pp. 219–227.

    Article  Google Scholar 

  14. Chaki, S. and Bourse, G., Guided ultrasonic waves for nondestructive monitoring of the stress levels in prestressed steel strands, Ultrasonics, 2009, vol. 49, no. 2, pp. 162–171.

    Article  CAS  Google Scholar 

  15. Wang, D., Song, Z., Wu, Y., et al., Ultrasonic wave based pressure measurement in small diameter pipeline, Ultrasoni-cs, 2015, vol. 63, pp. 1–6.

    Article  CAS  Google Scholar 

  16. Yao, B., Hongliang, Z., Zhiyao, H., et al., Ultrasonic pressure measurement in pressure vessels, Rev. Sci. Instru-m., 2014, vol. 85, no. 12, 125002–125002-10.

    Article  Google Scholar 

  17. Duenwald, S., Kobayashi, H., Frisch, K., et al., Ultrasound echo is related to stress and strain in tendon, J. Biomech., 2011, vol. 44, pp. 424–429.

    Article  Google Scholar 

  18. Thurston, R.N. and Brugger, K., Third order elastic constants and the velocity of small amplitude elastic waves in homogeneously stressed media, Phys. Rev., 1964, vol. 133, no. 6A, pp. 1604–1610.

    Article  Google Scholar 

  19. Rizzo, P. and di Scalea, F.L., Effect of frequency on the acoustoelastic response of steel bars, Exp. Tech., 2003, vol. 27, no. 6, pp. 40–43.

    Article  Google Scholar 

  20. Dean, T., Zhenqing, L., and Pengfei, H., Optimal mode and frequency thickness of guided waves nondestructive testing in pipes, J. TongJi Univ., 2004, vol. 32, no. 5, pp. 696–700.

    Google Scholar 

  21. Washer, G.A., Green, R.E., and Pond, R.B., Jr., Velocity constants for ultrasonic stress measurement in prestressing tendons, Res. Nondestr. Eval., 2002, vol. 14, pp. 81–94.

    Article  Google Scholar 

  22. Rizzo, P., Health monitoring of tendons and stay cables for civil structures, PhD Thesis, San-Diego: Univ. California, 2004.

Download references

ACKNOWLEDGMENTS

This project was supported by National Natural Science Foundation of China (no. 11662013) and the China Scholarship Council (CSC).

Author information

Authors and Affiliations

  1. College of Mechanical and Electrical Engineering, Inner Mongolia Agricultural University, 010018, Hohhot, China

    Yingsi Wu, Fei Liu & Wenliang Du

  2. Department of Mechanical Engineering, University of Alberta, T6G 2G8, Edmonton, Alberta, Canada

    Xiaodong Wang

Authors
  1. Yingsi Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaodong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wenliang Du
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Yingsi Wu, Fei Liu, Xiaodong Wang or Wenliang Du.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yingsi Wu, Liu, F., Wang, X. et al. Analysis of Guided Waves Dispersion and Acoustoelastic Effect in Stressed Waveguides by Eigenfrequency Method and Experimental Study. Russ J Nondestruct Test 55, 817–826 (2019). https://doi.org/10.1134/S106183091911010X

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S106183091911010X

Keywords:

Search

Navigation