Abstract
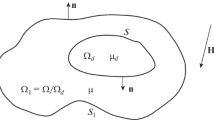
A method is proposed for solving the inverse problem of magnetostatics. The method has been investigated for metal-loss defects located on the side of a ferromagnetic plate opposite to magnetic transducers, without imposing any conditions on defect shape. The method is illustrated by numerical simulation. The ferromagnetic plate is magnetized in the direction of the abscissa axis; the dependence of the magnetic induction of metal on the applied external magnetic field corresponds to the linear segment of the magnetization curve. This configuration of defects and magnetizing system is typical, for example, of in-tube inspection problems. The problem is solved for the two-dimensional linear case. The applicability limits of the method are considered. The defects were simulated and the direct problem was solved using the FEMM software package. The program for constructing lines of force and solving the inverse problem of reconstructing magnetic field components has been written in the Scilab package of applied mathematical programs.
Similar content being viewed by others
References
Edens, B., Magnetic wall loss in plain English, Int. Pipe Insp. Assoc. Newsl., October 2005, pp. 112–114.
Dyakin, V.V., Matematicheskie osnovy klassicheskoi magnitostatiki (Mathematical Foundations of Classical Magnetostatics), Yekaterinburg: Ural Branch, Russ. Acad. Sci., 2016.
Krotov, L.N., Reconstruction of a media interface from the spatial distribution of a magnetic stray field: I. Analysis of the properties of the solution of the auxiliary direct problem (linear approximation), Russ. J. Nondestr. Test., 2004, vol. 40, no. 2, pp. 130–134.
Krotov, L.N., Reconstruction of a media boundary based on the spatial distribution of stray magnetic fields. II. Definition and method of solving the inverse geometric problem of magnetostatics, Russ. J. Nondestr. Test., 2004, vol. 40, no. 6, pp. 385–390.
Ramm, AG, Inverse Problems, Springer, 2005.
Alifanov, O.M., Artyukhin, E.A., and Rumyantsev, S.V., Ekstremal’nye metody resheniya nekorrektnykh zadach i ikh prilozheniya k obratnym zadacham teploobmena (Extremum Methods for Solving Ill-Posed Problems and Their Applications to Inverse Problems of Heat Transfer), Moscow: Nauka, 1988.
Khalileev, P.A., Patramanskii, B.V., Loskutov, V.E., Korzunin, G.S., and Shcherbinin, V.E., Detectability of defects in pipelines from different steel grades depending on their configuration, Russ. J. Nondestr. Test., 2000, vol. 36, no.8.
Zagidulin, R.V., Dyakin, V.V., Dudarev, M.S., and Shcherbinin, V.E., On the determination of the geometrical dimensions of a surface defect. Physical methods and devices for nondestructive testing, Tezisy Dokl. X Ural’skoi Nauchno-Tekh. Konf. (Proc. X Ural Sci. Tech. Conf.), Izhevsk, 1989.
Tikhonov, A.N. and Arsenin, V.Ya., Metody resheniya nekorrektnykh zadach (Methods for Solving Ill-Posed Problems), Moscow: Nauka, 1979.
Tikhonov, A.N., On the stability of inverse problems, Dokl. Akad. Nauk SSSR Mat. Fiz., 1943, vol. XXXIX, no. 5, pp. 195–198.
Phillips, D., A technique for the numerical solution of certain integral equations of the first kind, J. Assoc. Comp. Mash., 1962, no. 9, pp. 84–97.
Tikhonov, A.N., On the solution of ill-posed problems and the regularization method, Dokl. Akad. Nauk SSSR, 1963, vol. 151, no. 3, pp. 501–504.
Tikhonov, A.N. and Glazko, V.B., On the approximate solution of Fredholm integral equations of the first kind, Vychisl. Mat. Mat. Fiz., 1964, vol. 4, no. 3, pp. 564–571.
Hadamard, J., Sur les problèmes aux dérivées partielles et leur signification physique, Princeton Univ. Bull., 1902, pp. 49–52.
Kalitkin, N.N., Chislennye metody (Numerical Methods), St. Petersburg: BHV-Peterburg, 2011.
Verlan, A.F. and Sizikov, V.S., Integral’nye uravneniya: metody, algoritmy, programmy. Spravochnik (Integral Equations: Methods, Algorithms, Programs. A Reference Book), Kiev: Naukova Dumka, 1986.
Samarskii, A.A. and Vabishchevich, P.N., Chislennye metody resheniya obratnykh zadach matematicheskoi fiziki (Numerical Methods for Solving Inverse Problems of Mathematical Physics), Moscow: LKI, 2009.
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © Yu.L. Gobov, A.V. Nikitin, S.E. Popov, 2018, published in Defektoskopiya, 2018, No. 10, pp. 51–57.
Rights and permissions
About this article
Cite this article
Gobov, Y.L., Nikitin, A.V. & Popov, S.E. Solving the Inverse Geometric Problem of Magnetostatics for Corrosion Defects. Russ J Nondestruct Test 54, 726–732 (2018). https://doi.org/10.1134/S1061830918100042
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1061830918100042