Abstract
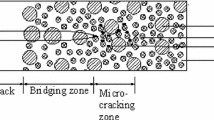
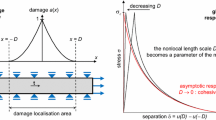
Based on the tenets of continuum micromechanics, a damage model is developed in the present work to investigate the effect of microcracking on the constitutive relations of cement based materials such as concrete. The model considers concrete as a two phase particulate composite consisting of coarse aggregates and mortar matrix. The microcracks are assumed to be present in the matrix material. Making use of Eshelby’s solution for equivalent inclusion, the stress and strain fields are evaluated at the mesoscale. A two step homogenization scheme is adopted to obtain the effective response of the composite. The crack density parameter is used as a damage variable in the formulation. Strain energy release rate, obtained from the micromechanical analysis, is used as the criterion for describing the propagation of microcracks. The effect of various mesoscopic parameters, such as aggregate content, elastic properties of the phases, microcrack density and fracture resistance of the matrix, on the overall behavior of concrete is demonstrated through a parametric study.
Similar content being viewed by others
References
Pensée, V., Kondo, D., and Dormieux, L., Micromechanical Analysis of Anisotropic Damage in Brittle Materials, J. Eng. Mech., 2002, vol. 128, no. 8, pp. 889–897.
Bažant, Z.P. and Planas, J., Fracture and Size Effect in Concrete and Other Quasibrittle Materials, Florida: CRC Press, 1997.
Shah, S.P., Swartz, S.E., and Ouyang, C., Fracture Mechanics of Concrete: Applications of Fracture Mechanics to Concrete, Rock and Other Quasi-Brittle Materials, New York: John Wiley & Sons, 1995.
Pensée, V. and Kondo, D., Micromechanics of Anisotropic Brittle Damage: Comparative Analysis between a Stress Based and a Strain Based Formulation, Mech. Mater., 2003, vol. 35, no. 8, pp. 747–761.
Zhu, Q.Z., Kondo, D., and Shao, J.F., Homogenization-Based Analysis of Anisotropic Damage in Brittle Materials with Unilateral Effect and Interactions between Microcracks, Int. J. Numer. Analyt. Meth. Geom., 2009, vol. 33, no. 6, pp. 749–772.
Zhu, Q.Z., Kondo, D., and Shao, J.F., Micromechanical Analysis of Coupling between Anisotropic Damage and Friction in Quasi Brittle Materials: Role of the Homogenization Scheme, Int. J. Solid. Struct., 2008, vol. 45, no. 5, pp. 1385–1405.
Zhu, Q.Z., Shao, J.F., and Kondo, D., A Micromechanics-Based Thermodynamic Formulation of Isotropic Damage with Unilateral and Friction Effects, Eur. J. Mech. A. Solid, 2011, vol. 30, no. 3, pp. 316–325.
Zhu, Q.Z. and Shao, J.F., A Refined Micromechanical Damage–Friction Model with Strength Prediction for Rock-Like Materials under Compression, Int. J. Solid. Struct., 2015, vol. 60, pp. 75–83.
Pichler, B., Hellmich, C.A., and Mang, H., A Combined Fracture-Micromechanics Model for Tensile Strain-Softening in Brittle Materials, Based on Propagation of Interacting Microcracks, Int. J. Numer. Analyt. Meth. Geom., 2007, vol. 31, no. 2, pp. 111–132.
Eshelby, J.D., The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems, Proc. R. Soc. Lond. A, 1957, vol. 241, no. 1226, pp. 376–396.
Nemat-Nasser, S. and Hori, M., Micromechanics: Overall Properties of Heterogeneous Materials, Amsterdam: North-Holland, 1993.
Budiansky, B. and O’Connell, R.J., Elastic Moduli of a Cracked Solid, Int. J. Solid. Struct., 1976, vol. 12, no. 2, pp. 81–97.
Bažant, P. and Oh, B.H., Efficient Numerical Integration on the Surface of a Sphere, Zeitschrift für Angewandte Mathematik und Mechanik (ZAMM), 1986, vol. 66, no. 1, pp. 37–49.
Mihai, I.C. and Jefferson, A.D., A Material Model for Cementitious Composite Materials with an Exterior Point Eshelby Microcrack Initiation Criterion, Int. J. Solid. Struct., 2011, vol. 48, no. 24, pp. 3312–3325.
Hordijk, D.A., Tensile and Tensile Fatigue Behaviour of Concrete; Experiments, Modelling and Analyses. V. 37, Heron: Stevin Laboratory and TNO Research, Delft, 1992.
Gopalaratnam, V.S. and Shah, S.P., Softening Response of Plain Concrete in Direct Tension, ACI J. Proc., 1985, vol. 82, no. 3, pp. 310–323.
Petersson, P.E., Fracture Energy of Concrete: Practical Performance and Experimental Results, Cement Concrete Res., 1980, vol. 10, no. 1, pp. 91–101.
Tasdemir, M.A. and Karihaloo, B.L., Effect of Aggregate Volume Fraction on the Fracture Parameters of Concrete: A Meso-Mechanical Approach, Mag. Concrete Res., 2001, vol. 53, no. 6, pp. 405–415.
Dhir, R.K. and Sangha, R.M., Development and Propagation of Microcracks in Plain Concrete, Matériaux et Construction, 1974, vol. 7, no. 1, pp. 17–23.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Dutta, S., Kishen, J.M.C. Micromechanical Damage Model for Plain Concrete Considering Propagation of Matrix Microcracks. Phys Mesomech 22, 96–106 (2019). https://doi.org/10.1134/S1029959919020024
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1029959919020024