Skip to main content
SpringerLink
Log in

A Potential-Based Smoothed Particle Hydrodynamics Approach for the Dynamic Failure Assessment of Compact and Granular Materials

  • Published:
Physical Mesomechanics Aims and scope Submit manuscript

Abstract

Computational simulation of solids has experienced a rapid development since the formulation of the finite element method. However a number of problems cannot be properly solved by using the finite element method because a severe mesh distortion in computations of Lagrangian scheme may arise for very large displacements, high speed impact, fragmentation, particulate solids, fluid-structure interaction, leading to lack of consistency between the numerical and the physical problem. The discretization of the problem domain with nodal points without any mesh connectivity would be useful to overcome this difficulty. Moreover the discrete nature of continuum matter—usually observed at the microscale—allows to adopt such a kind of discretization that is natural for granular materials and enables us to model very large deformations, handle damage—such as fracture, crushing, fragmentation, clustering—thanks to the variable interaction between particles.

In the context of meshless methods, smoothed particle hydrodynamics (SPH) is a meshfree particle method based on Lagrangian formulation that has been widely applied to different engineering fields. In the present paper a unified computational potential-based particle method for the mechanical simulation of continuum and granular materials under dynamic condition, is proposed and framed in the SPH-like approaches. The particleparticle and particle-boundary interaction is modelled through force functionals related to the nature of the material being analyzed (solid, granular,...); large geometrical changes of the mechanical system, such as fracture, clustering, granular flow can be easily modelled. Some examples are finally proposed and discussed to underline the potentiality of the approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a(r infl):

function of the influence radius of a particl

A ij , A 0, ij :

cross section area of the truss assumed beytween particles i and j and its reference value, respectively

b i :

body force component in the i-th direction

Cʹ:

tangent elastic tensor of the material

c(s):

function accounting for the no-penetration condition

d * :

equivalent diameter of two particles in contact

d i = 2r i :

diameter of the generic particle i

Eʹ(s), E 0 :

elastic modulus of a linear element that represents the material connecting the two particles i, j and corresponding reference value for s ≫ 0

E i :

elastic modulus of the generic particle i

\(\bar E\) :

equivalent Young modulus of the elastic contact between two particles

E tot(x) = Π(x):

total energy of the particle system

F ij (s):

generic force acting between a couple of particles at the effective distance s

F i, F d, F b, F e :

internal force, damping force, boundary and external force vectors, respectively

F tot, i :

vector of the total force acting on the particle i

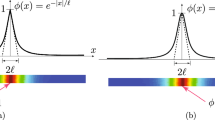
h :

smoothing length or support dimension

K(s):

stiffness of the particles bonding depending on their effective distance s

K n :

normal stiffness of the particle-boundary contact

m i , M :

mass of the particle i and mass matrix, respectively

n, t :

unit vectors normal and parallel to the tangential plane in the contact point between a generic particle and the boundary surface, respectively

P i :

force vector acting on particle i

q :

unit vector identifying the direction connecting the two particles centers

r :

distance between the centers of a couple of particles

\(\bar r\) :

average radius of a couple of particles

r infl :

radius of influence (or maximum interacting distance) of a particle r infl

r 0 :

distance between the centers of the particles at which F (r = r 0) → -∞

s, s e :

effective distance between particle surfaces and at the equilibrium state, respectively

sʹ = r - (d i /2 + d j/2):

distance between two particle surfaces

t, Δt :

time variable and time integration step amplitude, respectively

T n, T t :

particle-boundary contact surface forces normal and parallel to the tangential plane at the contact point, respectively

T t, ij :

tangential force between the colliding particles i, j

V p :

volume of the particle p

w :

displaced distance of one particle into another or into the contact surface

W (|x - x i |):

Kernel or smoothing function for the smoothed particle hydrodynamics method

x 0 :

position vector identifying the equilibrium state

x i , ẋ i , ẍ i :

position, velocity and acceleration vector of the particle i, respectively

x, ẋ, ẍ :

position, velocity and acceleration vector, respectively

α:

coefficient defining the maximum copenetration depth

ε ij (x i ):

strain tensor components at the point identified by x i

γ:

thickness of a soft layer added to the boundary surface in order to smooth the contact forces

δ(| x - x i |):

Dirac delta function placed at x i

\(\delta = \alpha \bar r\) :

maximum copenetration amount between two particles

σ ij :

stress tensor components

Φ(x), Φtot(x):

generic strain energy potential and potential of the particle system, respectively

λd :

damping coefficient

η:

viscosity coefficient

χ(w):

smoothing function for the force particle-boundary contact evaluation

μd :

coefficient of dynamic friction between particles and boundaries

μ md :

coefficient of dynamic friction between particles

ν i :

Poissons ratio of the generic particle i

ρ:

mass density.

References

  1. Clough, R.W., The Finite Element Method in Structural Mechanics, in Stress Analysis, Zienkiewicz, O.C. and Holister, G.S., Eds., London: Wiley, 1965, pp. 85–119.

    Google Scholar 

  2. Oden, J.T., An Introduction to the Mathematical Theory of Finite Elements, New York: Wiley, 1976.

    MATH  Google Scholar 

  3. Dow, J.O., Jones, M.S., and Harwood, S.A., A Generalized Finite Difference Method for Solid Mechanics, Num. Meth. Partial Diff Eqs., 1990, vol. 6, no. 2, pp. 137–152.

    Article  MATH  Google Scholar 

  4. Wrobel, L.C. and Aliabadi, M.H., The Boundary Element Method, Chichester: Wiley, 2002.

    Google Scholar 

  5. Belytschko, T., Krongauz, Y., Organ, D., Fleming, M., and Krysl, P., Meshless Methods: An Overview and Recent Developments, Comp. Meth. Appl. Mech. Engng., 1996, vol. 139, no. 1-4, pp. 3–47.

    Article  MATH  Google Scholar 

  6. Sukumar, N., Moran, B., and Belytschko, T., The Natural Element Method in Solid Mechanics, Int. J. Num. Meth. Engng., 1998, vol. 43, no. 5, pp. 839–887.

    Article  MATH  MathSciNet  Google Scholar 

  7. Lucy, L.B., A Numerical Approach to the Testing of the Fission Hypothesis, Astron. J., 1977, vol. 82, pp. 1013–1024.

    Article  ADS  Google Scholar 

  8. Gingold, R.A. and Monaghan, J.J., Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars, Mon. Not. R. Astron. Soc., 1977, vol. 181, pp. 375–389.

    Article  ADS  MATH  Google Scholar 

  9. Benz, W., Smooth Particle Hydrodynamics: A Review, in Numerical Modeling of Non-Linear Stellar Pulsation, Problems and Prospects, Buchler, J.R., Ed., Boston: Kluwer Academic, 1990.

    Google Scholar 

  10. Monaghan, J.J., Why Particle Methods Work. SIAM, J. Sci. Stat. Comput., 1982, vol. 3, no. 4, pp. 422–433.

    Article  MATH  MathSciNet  Google Scholar 

  11. Monaghan, J.J., Smoothed Particle Hydrodynamics, Annu. Rev. Astron. Astrophys., 1992, vol. 30, pp. 543–574.

    Article  ADS  Google Scholar 

  12. Monaghan, J.J., SPH Elastic Dynamics, Comp. Meth. Appl. Mech. Engng., 2001, vol. 190, pp. 6641–6662.

    Article  MATH  Google Scholar 

  13. Monaghan, J.J., Smoothed Particle Hydrodynamics, Rep. Prog. Phys., 2005, vol. 68, pp. 1703–1759.

    Article  ADS  MathSciNet  Google Scholar 

  14. Monaghan, J.J., Smoothed Particle Hydrodynamics and its Diverse Applications, Annu. Rev. Fluid Mech., 2012, vol. 44, pp. 323–346.

    Article  ADS  MathSciNet  Google Scholar 

  15. Li, S. and Liu, W.K., Meshfree and Particle Methods and Their Applications, Appl. Mech. Rev., 2002, vol. 55, no. 1, pp. 1–34.

    Article  ADS  Google Scholar 

  16. Bui, H.H., Fukagawa, R., Sako, K., and Ohno, S., Lagrangian Meshfree Particles Method (SPH) for Large Deformation and Failure Flows of Geomaterial Using Elastic-Plastic Soil Constitutive Model, Int. J. Num. An. Meth. Geomech., 2008, vol. 32, no. 12, pp. 1537–1570.

    Article  MATH  Google Scholar 

  17. Harthong, B., Jérier, J.-F., Dorémus, P., Imbault, D., and Donzé, F.-V., Modeling of High-Density Compaction of Granular Materials by the Discrete Element Method, Int. J. Solids Struct., 2009, vol. 46, pp. 3357–3364.

    Article  MATH  Google Scholar 

  18. Pana, W., Tartakovskya, A.M., and Monaghan, J.J., Smoothed Particle Hydrodynamics Non-Newtonian Model for Ice-Sheet and Ice-Shelf Dynamics, J. Comput. Phys., 2013, vol. 242, pp. 828–842.

    Article  ADS  MathSciNet  Google Scholar 

  19. Bessa, M.A., Foster, J.T., Belytschko, T., and Liu, W.K., A Meshfree Unification: Reproducing Kernel Peridynamics, Comput. Mech., 2014, vol. 53, no. 6, pp. 1251–1264.

    Article  MATH  MathSciNet  Google Scholar 

  20. Braun, M. and Fernandez-Saez, J., A New 2D Discrete Model Applied to Dynamic Crack Propagation in Brittle Materials, Int. J. Solids Struct., 2014, vol. 51, pp. 3787–3797.

    Article  Google Scholar 

  21. Curtin, W.A. and Miller, R.E., Atomistic/Continuum Coupling in Computational Materials Science, Model. Simul. Mater. Sci. Eng., 2003, vol. 11, pp. R33–R68.

    Article  ADS  Google Scholar 

  22. Liu, B., Huang, Y., Jiang, H., Qu, S., and Hwang, K.C., The Atomic-Scale Finite Element Method, Comp. Meth. Appl. Mech. Engng., 2004, vol. 193, pp. 1849–1864.

    Article  MATH  Google Scholar 

  23. Hoover, W.G., Computational Physics with Particles—Nonequilibrium Molecular Dynamics and Smooth Particle Applied Mechanics, Comput. Meth. Sci. Tech., 2007, vol. 13, pp. 83–93.

    Article  MathSciNet  Google Scholar 

  24. Cundall, P.A. and Strack, O.D.L., A Discrete Numerical Model for Granular Assemblies, Geotechnique, 1979, vol. 29, pp. 47–65.

    Article  Google Scholar 

  25. Oóate, E., Idelson, S.R., Del Pin, F., and Aubry, R., The Particle Finite Element Method. An Overview, Int. J. Comput. Meth., 2004, vol. 1, no. 2, pp. 267–307.

    Article  Google Scholar 

  26. Tavarez, F.A. and Plesha, M.E., Discrete Element Method for Modelling Solid and Particulate Materials, Int. J. Num. Meth. Engng., 2007, vol. 70, pp. 379–404.

    Article  MATH  Google Scholar 

  27. Particle-Based Methods: Fundamentals and Applications, Oóate, E. and Owen, R., Eds., Springer, 2011.

  28. De Gennes, P.G., Granular Matter: a Tentative View, Rev. Modern Phys., 1999, vol. 71, pp. S374–S382.

    Article  Google Scholar 

  29. D’Addetta, G.A., Kun, F., and Ramm, E., On the Application of a Discrete Model to the Fracture Process of Cohesive Granular Materials, Granular Matter., 2002, vol. 4, pp. 77–90.

    Article  MATH  Google Scholar 

  30. Rycroft, C.H., Kamrin, K., Bazant, M.Z., Assessing Continuum Postulates in Simulations of Granular Flow, J. Mech. Phys. Sol., 2009, vol. 57, pp. 828–839.

    Article  ADS  Google Scholar 

  31. Guzev, M.A. and Dmitriev, A.A., Bifurcational Behavior of Potential Energy in a Particle System, Phys. Mesomech., 2013, vol. 16, no. 4, pp. 287–293.

    Article  Google Scholar 

  32. Krivtsov, A., Molecular Dynamics Simulation of Impact Fracture in Polycrystalline Materials, Meccanica, 2003, vol. 38, pp. 61–70.

    Article  MATH  Google Scholar 

  33. Kuzkin, V.A., Krivtsov, A.M., Jones, R.E., and Zimmerman, J.A., Material Frame Representation of Equivalent Stress Tensor for Discrete Solids, Phys. Mesomech., 2015, vol. 18, no. 1, pp. 13–23.

    Article  Google Scholar 

  34. Obermayr, M., Dressler, K., Vrettos, C., and Eberhard, P., A Bonded-Particle Model for Cemented Sand, Comp. Geotechnics, 2013, vol. 49, pp. 299–313.

    Article  Google Scholar 

  35. Brilliantov, N., Spahn, F., Hertzsch, J., and Poshel, T., Model for Collision in Granular Gases, Phys. Rev E, 1996, vol. 53, pp. 5382–5392.

    Article  ADS  Google Scholar 

  36. Aubry, R., Idelsohn, S.R., and Onate, E., Particle Finite Element Method in Fluid Mechanics Including Thermal Convection-Diffusion, Comput. Struct., 2005, vol. 83, pp. 1459–1475.

    Article  Google Scholar 

  37. Morse, P.M., Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels, Phys. Rev., 1930, vol. 34, pp. 57–64.

    Article  ADS  Google Scholar 

  38. Liu, W.K., Jun, S., and Qian, D., Computational Nanomechanics of Materials, in Theoretical and Computational Nanotechnology, Rieth, M. and Schommers, W., Eds., Stevenson Ranch, CA: Am. Sci. Publ., 2005.

    Google Scholar 

  39. Brighenti, R. and Corbari, N., Dynamic Failure in Brittle Solids and Granular Matters: a Force Potential-Based Particle Method, J. Numer. Meth. Engng., 2015, doi 10.1002/nme.4998.

    Google Scholar 

  40. Verlet, L., Computer Experiments on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules, Phys. Rev., 1967, vol. 159, pp. 98–103.

    Article  ADS  Google Scholar 

  41. O’Sullivan, C. and Bray, J.D., Selecting a Suitable Time Step for Discrete Element Simulations that Use the Central Difference Time Integration Scheme, Engng. Comput., 2004, vol. 21, pp. 278–303.

    Article  MATH  Google Scholar 

  42. Lim, K-W., Krabbenhoft, K., and Andrade, J.E., A Contact Dynamics Approach to the Granular Element Method, Comp. Meth. Appl. Mech. Engng., 2014, vol. 268, pp. 557–573.

    Article  ADS  MATH  MathSciNet  Google Scholar 

  43. Coetzee, C.J., Discrete and Continuum Modelling of Soil Cutting, Comp. Part. Mech., 2014, vol. 1, no. 4, pp. 409–423.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Parma, Parma, 43100, Italy

    R. Brighenti & N. Corbari

Authors
  1. R. Brighenti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. Corbari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Brighenti.

Additional information

Original Text © R. Brighenti, N. Corbari, 2015, published in Fizicheskaya Mezomekhanika, 2015, Vol. 18, No. 5, pp. 124-136.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Brighenti, R., Corbari, N. A Potential-Based Smoothed Particle Hydrodynamics Approach for the Dynamic Failure Assessment of Compact and Granular Materials. Phys Mesomech 18, 402–415 (2015). https://doi.org/10.1134/S1029959915040128

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1029959915040128

Keywords

Search

Navigation