Skip to main content
SpringerLink
Log in

Influence of Monotonization on the Spectral Resolution of Bicompact Schemes in the Inviscid Taylor–Green Vortex Problem

  • MATHEMATICAL PHYSICS
  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

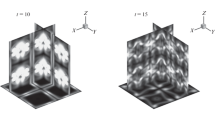
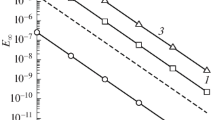
For the three-dimensional Euler equations, a locally one-dimensional bicompact scheme having the fourth order of approximation in space and the second order of approximation in time is considered. The scheme is used in the Taylor–Green vortex problem in an inviscid perfect gas to examine the degree to which a conservative limiting (monotonization) method applied to bicompact schemes affects their theoretically high spectral resolution. Two parallel computational algorithms for locally one-dimensional bicompact schemes are proposed. One of them is used for carrying out computations. It is shown that, in the case of monotonization, the chosen bicompact scheme resolves 70–85% of the kinetic energy spectrum of the fluid. The scheme is compared with high-order accurate WENO5 schemes in terms of the behavior of kinetic energy and enstrophy. It is demonstrated that the bicompact scheme has noticeably lower dissipation and more weakly suppresses medium-scale eddies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.

Similar content being viewed by others

REFERENCES

  1. J. C. Tannehill, D. A. Anderson, and R. H. Pletcher, Computational Fluid Mechanics and Heat Transfer (McGraw-Hill, New York, 1984).

    MATH  Google Scholar 

  2. S. Kawai and S. K. Lele, “Large-eddy simulation of jet mixing in supersonic crossflows,” AIAA J. 48 (9), 2063–2083 (2010).

    Article  Google Scholar 

  3. J. R. Bull and A. Jameson, “Simulation of the Taylor–Green vortex using high-order flux reconstruction schemes,” AIAA J. 53 (9), 2750–2761 (2015).

    Article  Google Scholar 

  4. P. Sagaut, Large Eddy Simulation for Incompressible Flows, 3rd ed. (Springer, Berlin, 2006).

  5. R. C. Moura, G. Mengaldo, J. Peiró, and S. J. Sherwin, “On the eddy-resolving capability of high-order discontinuous Galerkin approaches to implicit LES under-resolved DNS of Euler turbulence,” J. Comput. Phys. 330, 615–623 (2017).

    Article  MathSciNet  Google Scholar 

  6. D. Flad, A. Beck, and P. Guthke, “A large eddy simulation method for DGSEM using non-linearly optimized relaxation filters,” J. Comput. Phys. 408, 109303 (2020).

  7. D. Drikakis, C. Fureby, F. Grinstein, and D. Youngs, “Simulation of transition and turbulence decay in the Taylor–Green vortex,” J. Turbul. 8 (20), 1–12 (2007).

    Article  Google Scholar 

  8. X. Liu, S. Zhang, H. Zhang, and C.-W. Shu, “A new class of central compact schemes with spectral-like resolution I: Linear schemes,” J. Comput. Phys. 248, 235–256 (2013).

    Article  MathSciNet  Google Scholar 

  9. M. de la Llave Plata, V. Couaillier, and M.-C. Pape, “On the use of a high-order discontinuous Galerkin method for DNS and LES of wall-bounded turbulence,” Comput. Fluids 176, 320–337 (2018).

  10. G. Gassner and A. Beck, “On the accuracy of high-order discretizations for underresolved turbulence simulations,” Theor. Comput. Fluid. Dyn. 27, 221–237 (2013).

    Article  Google Scholar 

  11. L. T. Diosady and S. M. Murman, “DNS of flows over periodic hills using a discontinuous-Galerkin spectral-element method,” 44th AIAA Fluid Dynamics Conference (2014).

  12. G.-S. Jiang and C.-W. Shu, “Efficient implementation of weighted ENO schemes,” J. Comput. Phys. 126 (1), 202–228 (1996).

    Article  MathSciNet  Google Scholar 

  13. Z. Wang, J. Zhu, L. Tian, and N. Zhao, “A low dissipation finite difference nested multi-resolution WENO scheme for Euler/Navier–Stokes Equations,” J. Comput. Phys. 429, 110006 (2021).

  14. R. Borges, M. Carmona, B. Costa, and W. S. Don, “An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws,” J. Comput. Phys. 227 (6), 3191–3211 (2008).

    Article  MathSciNet  Google Scholar 

  15. V. M. Goloviznin, M. A. Zaitsev, S. A. Karabasov, and I. A. Korotkin, New CFD Algorithms for Multiprocessor Computer Systems (Mosk. Gos. Univ., Moscow, 2013) [in Russian].

    Google Scholar 

  16. V. F. Tishkin, V. A. Gasilov, N. V. Zmitrenko, et al., “Modern methods of mathematical modeling of the development of hydrodynamic instabilities and turbulent mixing,” Math. Models Comput. Simul. 13 (2), 311–327 (2021).

    Article  Google Scholar 

  17. K. Grimich, P. Cinnella, and A. Lerat, “Spectral properties of high-order residual-based compact schemes for unsteady compressible flows,” J. Comput. Phys. 252, 142–162 (2013).

    Article  MathSciNet  Google Scholar 

  18. A. I. Tolstykh, Compact Finite Difference Schemes and Application in Aerodynamic Problems (Nauka, Moscow, 1990) [in Russian].

    Google Scholar 

  19. A. I. Tolstykh, High Accuracy Compact and Multioperator Approximations for Partial Differential Equations (Nauka, Moscow, 2015) [in Russian].

    Google Scholar 

  20. M. D. Bragin and B. V. Rogov, “Minimal dissipation hybrid bicompact schemes for hyperbolic equations,” Comput. Math. Math. Phys. 56 (6), 947–961 (2016).

    Article  MathSciNet  Google Scholar 

  21. M. D. Bragin and B. V. Rogov, “On exact dimensional splitting for a multidimensional scalar quasilinear hyperbolic conservation law,” Dokl. Math. 94 (1), 382–386 (2016).

    Article  MathSciNet  Google Scholar 

  22. B. V. Rogov and M. D. Bragin, “On spectral-like resolution properties of fourth-order accurate symmetric bicompact schemes,” Dokl. Math. 96 (1), 140–144 (2017).

    Article  MathSciNet  Google Scholar 

  23. A. V. Chikitkin and B. V. Rogov, Preprint No. 177, IPM RAN (Keldysh Inst. of Applied Mathematics, Russian Academy of Sciences, Moscow, 2018).

  24. A. V. Chikitkin and B. V. Rogov, “Family of central bicompact schemes with spectral resolution property for hyperbolic equations,” Appl. Numer. Math. 142, 151–170 (2019).

    Article  MathSciNet  Google Scholar 

  25. B. V. Rogov, “Dispersive and dissipative properties of the fully discrete bicompact schemes of the fourth order of spatial approximation for hyperbolic equations,” Appl. Numer. Math. 139, 136–155 (2019).

    Article  MathSciNet  Google Scholar 

  26. M. D. Bragin and B. V. Rogov, “Conservative limiting method for high-order bicompact schemes as applied to systems of hyperbolic equations,” Appl. Numer. Math. 151, 229–245 (2020).

    Article  MathSciNet  Google Scholar 

  27. M. D. Bragin and B. V. Rogov, “Bicompact schemes for gas dynamics problems: Introducing complex domains using the free boundary method,” Komp’yut. Issled. Model. 12 (3), 487–504 (2020).

    Google Scholar 

  28. M. D. Bragin and B. V. Rogov, “High-order bicompact schemes for numerical modelling of multispecies multi-reaction gas flows,” Mat. Model. 32 (6), 21–36 (2020).

    MathSciNet  MATH  Google Scholar 

  29. M. E. Brachet, D. I. Meiron, S. A. Orszag, et al., “Small-scale structure of the Taylor–Green vortex,” J. Fluid Mech. 130, 411–452 (1983).

    Article  Google Scholar 

  30. R. Alexander, “Diagonally implicit Runge–Kutta methods for stiff O.D.E.'s,” SIAM J. Numer. Anal. 14 (6), 1006–1021 (1977).

    Article  MathSciNet  Google Scholar 

  31. G. I. Marchuk, Splitting Methods (Nauka, Moscow, 1988) [in Russian].

    Google Scholar 

  32. S. A. Lupin and M. A. Posypkin, Technologies of Parallel Programming (Infra-M, Moscow, 2011) [in Russian].

Download references

Funding

This work was supported by the Russian Science Foundation, project no. 21-11-00198.

Author information

Authors and Affiliations

  1. Federal Research Center Keldysh Institute of Applied Mathematics, Russian Academy of Sciences, 125047, Moscow, Russia

    M. D. Bragin

Authors
  1. M. D. Bragin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. D. Bragin.

Ethics declarations

The author declares that he has no conflicts of interest.

Additional information

To the blessed memory of B.V. Rogov

Translated by I. Ruzanova

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bragin, M.D. Influence of Monotonization on the Spectral Resolution of Bicompact Schemes in the Inviscid Taylor–Green Vortex Problem. Comput. Math. and Math. Phys. 62, 608–623 (2022). https://doi.org/10.1134/S0965542522040030

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542522040030

Keywords:

Search

Navigation