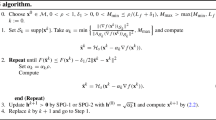Abstract
This paper describes a new efficient conjugate subgradient algorithm which minimizes a convex function containing a least squares fidelity term and an absolute value regularization term. This method is successfully applied to the inversion of ill-conditioned linear problems, in particular for computed tomography with the dictionary learning method. A comparison with other state-of-art methods shows a significant reduction of the number of iterations, which makes this algorithm appealing for practical use.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
F. Bach, R. Jenatton, J. Mairal, and G. Obozinski, “Optimization with sparsity-inducing penalties,” Foundations Trends Machine Learning 4 (1), 1–106 (2011).
A. N. Tikhonov, “On the stability of inverse problems,” Dokl. Akad. Nauk SSSR 5 (39), 195–198 (1943).
A. Chambolle and T. Pock, “A first-order primal-dual algorithm for convex problems with applications to imaging,” J. Math. Imaging Vision 40 (1), 120–145 (2011).
E. Y. Sidky, J. H. Jørgensen, and X. Pan, “Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle–Pock algorithm,” Phys. Med. Biol. 57 (10), 3065–3091 (2012).
P. L. Combettes and J.-C. Pesquet, “Proximal Splitting Methods in Signal Processing,” ArXiv e-prints, Dec. 2009.
R. Tibshirani, “Regression shrinkage and selection via the lasso,” J. R. Stat. Soc. Ser. B (Methodological) 58 (1), 267–288 (1996).
L. I. Rudin, S. Osher, and E. Fatemi, “Nonlinear total variation based noise removal algorithms,” Phys. D: Nonlinear Phenom. 60 (1–4), 259–268 (1992).
I. W. Selesnick and M. A. T. Figueiredo, “Signal restoration with overcomplete wavelet transforms: Comparison of analysis and synthesis priors,” Proc. SPIE 7446, Wavelets XIII, 74460D (September 4, 2009).
A. Beck and M. Teboulle, “Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems,” IEEE Trans. Image Process. 18, 2419–2434 (2009).
Y. Nesterov, “A method of solving a convex programming problem with convergence rate O(1/sqr(k)),” Sov. Math. Dokl. 27, 372–376 (1983).
S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Found. Trends Machine Learn. 3 (1), 1–122, (2011).
S. Boyd, L. Xiao, and A. Mutapcic, “Subgradient methods,” Notes for EE392o (Stanford Univ. 2003).
S. Bubeck, “Theory of convex optimization for machine learning,” arXiv:1405.4980 (2014).
A. Mirone and P. Paleo, “Python script: Csg.py.” https://github.com/pierrepaleo/csg
A. Mirone, E. Brun, and P. Coan, “A dictionary learning approach with overlap for the low dose computed tomography reconstruction and its vectorial application to differential phase tomography,” PLoS ONE 9 (12), e114325 (2014). doi 10.1371/journal.pone.0114325
E. J. Candés, J. K. Romberg, and T. Tao, “Stable signal recovery from incomplete and inaccurate measurements,” Commun. Pure Appl. Math. 59 (8), 1207–1223 (2006).
P. Paleo and A. Mirone, “Ring artifacts correction in compressed sensing tomographic reconstruction,” arXiv:1502.01480 (2015).
A. Mirone, E. Brun, E. Gouillart, P. Tafforeau, and J. Kieffer, “The PyHST2 hybrid distributed code for high speed tomographic reconstruction with iterative reconstruction and a priori knowledge capabilities,” Nuclear Instrum. Methods Phys. Res. Sect B: Beam Interactions Materials Atoms 324, 41–48 (2014).
Author information
Authors and Affiliations
Corresponding author
Additional information
The article is published in the original.
Rights and permissions
About this article
Cite this article
Mirone, A., Paleo, P. A conjugate subgradient algorithm with adaptive preconditioning for the least absolute shrinkage and selection operator minimization. Comput. Math. and Math. Phys. 57, 739–748 (2017). https://doi.org/10.1134/S0965542517040066
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0965542517040066