Skip to main content
SpringerLink
Log in

Effective averaging of stochastic radiative models based on Monte Carlo simulation

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

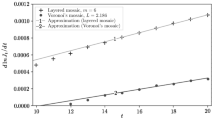
Based on the Monte Carlo simulation and probabilistic analysis, stochastic radiative models are effectively averaged; that is, deterministic models that reproduce the mean probabilities of particle passage through a stochastic medium are constructed. For this purpose, special algorithms for the double randomization and conjugate walk methods are developed. For the numerical simulation of stochastic media, homogeneous isotropic Voronoi and Poisson mosaic models are used. The parameters of the averaged models are estimated based on the properties of the exponential distribution and the renewal theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. A. Mikhailov, “Asymptotic estimates of the mean probability of radiative transfer through an exponentially correlated stochastic medium,” Izv. Atmos. Ocean. Phys. 48, 618–624 (2012).

    Article  Google Scholar 

  2. J. Serra, Image Analysis and Mathematical Morphology (Academic, London, 1982).

    MATH  Google Scholar 

  3. P. Switzer, “A random set process in the plane with a Markovian property,” Ann. Math. Statist. 36, 1859–1863 (1965).

    Article  MathSciNet  MATH  Google Scholar 

  4. E. N. Gilbert, “Random subdivisions of space into crystals,” Ann. Math. Statist., No. 33, 958–972 (1962).

    Article  MathSciNet  MATH  Google Scholar 

  5. A. Yu. Ambos and G. A. Mikhailov, “Statistical modelling of the exponentially correlated multivariate random field,” Rus. J. Num. Anal. Math. Model. 26 (3), 213–232 (2011).

    MathSciNet  MATH  Google Scholar 

  6. S. M. Prigarin, Numerical Simulation of Random Processes and Fields (Inst. of Computational Mathematics and Mathematical Geophysics, Siberian Branch, Russian Academy of Sciences, Novosibirsk, 2005) [in Russian].

    Google Scholar 

  7. W. A. Coleman, “Mathematical verification of a certain Monte Carlo sampling technique and applications of the technique to radiation transport problems,” Nucl. Sci. Eng. 32 (1), 76–81 (1968).

    Article  Google Scholar 

  8. G. Marchuk, G. Mikhailov, M. Nazaraliev, R. Darbinjan, B. Kargin, and B. Elepov, The Monte Carlo Methods in Atmospheric Optics (Nauka, Novosibirsk, 1976; Springer, Berlin, 1980).

    Google Scholar 

  9. G. A. Mikhailov, Optimization of weighted Monte Carlo methods (Nauka, Moscow, 1987; Springer, Berlin, 1992).

    Google Scholar 

  10. E. M. Feigel’son and L. D. Krasnokutskaya, Solar Radiation Fluxes and Clouds (Gidrometeoizdat, Leningrad, 1978) [in Russian].

    Google Scholar 

  11. W. Feller, An Introduction to Probability Theory and Its Applications (Wiley, New York, 1967; Mir, Moscow, 1967).

    MATH  Google Scholar 

  12. I. A. Ibragimov and Yu. V. Linnik, Independent and Stationary Related Quantities (Nauka, Moscow, 1965) [in Russian].

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Mathematics and Mathematical Geophysics, Siberian Branch, Russian Academy of Sciences, pr. Akademika Lavrent’eva 6, Novosibirsk, 630090, Russia

    A. Yu. Ambos & G. A. Mikhailov

Authors
  1. A. Yu. Ambos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. A. Mikhailov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Yu. Ambos.

Additional information

Original Russian Text © A.Yu. Ambos, G.A. Mikhailov, 2016, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2016, Vol. 56, No. 5, pp. 896–908.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ambos, A.Y., Mikhailov, G.A. Effective averaging of stochastic radiative models based on Monte Carlo simulation. Comput. Math. and Math. Phys. 56, 881–893 (2016). https://doi.org/10.1134/S0965542516050055

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542516050055

Keywords

Search

Navigation