Skip to main content
SpringerLink
Log in

Opening gaps in the spectrum of the water-wave problem in a periodic channel

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

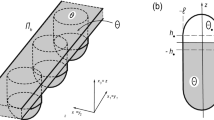
It is shown that the essential spectrum of a problem in the theory of linear water waves in a periodic channel can contain any prescribed number of gaps. One of such waveguides consists of a periodic family of identical ponds of unit size connected by narrow shallow channels. The effect of gap opening is achieved by decreasing a geometric parameter describing the size of these channels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. J. Stoker, Water Waves. The Mathematical Theory with Applications, Reprint of the 1957 Original (John Willey & Sons, Inc, New York, 1992).

    MATH  Google Scholar 

  2. N. Kuznetsov, V. Maz’ya, and B. Vainberg, Linear Water Waves (Cambridge University Press, Cambridge, 2002).

    Book  MATH  Google Scholar 

  3. D. A. Indeitsev, N. G. Kuznetsov, O. V. Motygin, and Yu. A. Mochalova, Localization of Linear Waves (SPb. Gos. Univ., St. Petersburg, 2007) [in Russian].

    Google Scholar 

  4. O. A. Ladyzhenskaya, The Boundary Value Problems of Mathematical Physics (Nauka, Moscow, 1973; Springer, New York, 1985).

    Google Scholar 

  5. S. A. Nazarov, “On Crowding of Point Spectrum on the Continuous One in Problems of Linear Water-Wave Theory,” Zapiski Nauchn. Seminarov POMI 348, 99–126 (2007).

    Google Scholar 

  6. S. A. Nazarov, “Concentration of Trapped Modes in Problems of the Linearized Theory of Water Waves,” Mat. Sb. 199 (12), 53–78 (2008).

    Google Scholar 

  7. M. Sh. Birman and M. Z. Solomyak, Spectral Theory ofSelf-Adjoint Operators in Hilbert Space (Leningr. Gos. Univ., Leningrad, 1980) [in Russian].

    Google Scholar 

  8. I. M. Gel’fand, “Expansion in Eigenfunctions of Equations with Periodic Coefficients,” Dokl. Akad. Nauk SSSR 73, 1117–1120 (1950).

    MATH  Google Scholar 

  9. P. A. Kuchment, “Floquet Theory for Partial Differential Equations,” Usp. Mat. Nauk 37, 3–52 (1982).

    MathSciNet  Google Scholar 

  10. S. A. Nazarov and B. A. Plamenevsky, Elliptic Problems in Domains with Piecewise Smooth Boundaries (Nauka, Moscow, 1991; W. de Gruyter, Berlin, 1994).

    Google Scholar 

  11. P. Kuchment, Floquet Theory for Partial Differential Equations (Birchäuser, Basel, 1993).

    MATH  Google Scholar 

  12. T. Kato, Perturbation Theory for Linear Operators (Springer, Berlin, 1966; Mir, Moscow, 1972).

    MATH  Google Scholar 

  13. M. Reed and B. Saimon, Methods of Modern Mathematical Physics, Vol. 4: Analysis of Operators (Academic, New York, 1972; Mir, Moscow, 1982).

    Google Scholar 

  14. M. M. Skriganov, “Geometric and Arithmetic Methods in the Spectral Theory of Multidimensional Periodic Operators,” in Tr. Mat. Inst. im. V.A. Steklova, Akad. Nauk SSSR (Nauka, Leningrad, 1985), Vol. 171.

    Google Scholar 

  15. V. A. Kondrat’ev, “Boundary Value Problems for Elliptic Equations in Domains with Conical or Corner Points,” Tr. Mos. Mat. Ob-Va 16, 219–292 (1963).

    Google Scholar 

  16. V. G. Maz’ya and B. A. Plamenevskii, “On the Coefficients in the Asymptotics of Solutions of Elliptic Boundary Value Problems in Domains with Conical Points,” Math. Nachr. 76, 29–60 (1977).

    Article  MATH  MathSciNet  Google Scholar 

  17. V. G. Maz’ya and B. A. Plamenevskii, “Estimates in Lp and H:O Classes and the Miranda-Agmon Maximum Principle for Solutions of Elliptic BVP in Domains with Singular Points on the Boundary,” Math. Nachr. 77, 25–82 (1977).

    Google Scholar 

  18. S. A. Nazarov, “A Polynomial Property of Self-Adjoint Elliptic Boundary Value Problems and an Algebraic Description of Their Attributes,” Usp. Mat. Nauk 54 (5), 77–142 (1999).

    Google Scholar 

  19. V. A. Kozlov, V. G. Maz’ya, and J. Rossmann, Elliptic Boundary Value Problems in Domains with Point Singularities (Amer. Math. Soc., Providence, 1997).

    MATH  Google Scholar 

  20. S. A. Nazarov, “Elliptic Boundary Value Problems with Periodic Coefficients in a Cylinder,” Izv. Akad. Nauk SSSR, Ser. Mat. 45 (1), 101–112 (1981).

    MATH  MathSciNet  Google Scholar 

  21. S. A. Nazarov, “Properties of Spectra of Boundary Value Problems in Cylindrical and Quasicylindrical Domain,” in Sobolev Spaces in Mathematics. Int. Mathematical Series, Vol. 9, pp. 261–309.

  22. I. Ts. Gokhberg and M. G. Krein, Introduction to the Theory of Linear Non-Self-Adjoint Operators (Nauka, Moscow, 1965; American Mathematical Society, Providence, R.I., 1969).

    Google Scholar 

  23. V. A. Kondrat’ev, “On the Smoothness of Solutions to the Dirichlet Problem for the Second-Order Elliptic Equation in a Neighborhood of an Edge,” Differ. Uravn. 6, 1831–1843 (1970).

    MATH  Google Scholar 

  24. V. A. Kondrat’ev, “Singularities of Solutions to the Dirichlet Problem for the Second-Order Elliptic Equation in a Neighborhood of an Edge,” Differ. Uravn. 13, 2026–2032 (1977).

    MATH  Google Scholar 

  25. V. G. Maz’ya and B. A. Plamenevskii, “On the Ellipticity of Boundary Value Problems in Domains with a Piece-wise Smooth Boundary,” in Proc. of the Symposium on Mechanics of Continua and Related Problems (Metsniereba, Tbilisi, 1973), Vol. 1, pp. 171–181 [in Russian].

    Google Scholar 

  26. S. A. Nazarov and B. A. Plamenevskii, “Neumann Problem for Self-Adjoint Elliptic Systems in a Domain with Piecewise Smooth Boundary,” Tr. Leningr. Mat. Ob-Va 1, 174–211 (1990).

    MATH  MathSciNet  Google Scholar 

  27. M. Dauge, “Elliptic Boundary Value Problems on Corner Domains. Smoothness and Asymptotics of Solutions,” Lect. Notes in Math., 1341 (Springer, Berlin, 1988).

  28. P. Grisvard, Singularities in Boundary Value Problems (Masson, Springer, Paris, 1992).

    MATH  Google Scholar 

  29. V. A. Nikishkin, “Singularities of Solutions to the Dirichlet Problem for the Second-Order Elliptic Equation in a Neighborhood of an Edge,” Vestn. Mosk. Univ., No. 2, 51–62 (1979).

    MathSciNet  Google Scholar 

  30. V. G. Maz’ya and J. Rossmann, “öber die Asymptotik der Lösungen elliptischer Randwertaufgaben in der Umgebung von Kanten,” Math. Nachr. 138, 27–53 (1988).

    Article  MATH  MathSciNet  Google Scholar 

  31. S. A. Nazarov and B. A. Plamenevskii, “Self-Adjoint Problems subject to Radiation Conditions on the Boundary Edges,” Algebra Analiz 4 (3), 196–225 (1992).

    MathSciNet  Google Scholar 

  32. S. A. Nazarov and B. A. Plamenevskii, “Generalized Green’s Formula for Elliptic Problems in Domains with Edges,” in Problems of Mathematical Analysis, No. 13 (SPb Gos. Univ., St. Petersburg, 1992), pp. 106–147 [in Russian].

    Google Scholar 

  33. S. A. Nazarov and B. A. Plamenevskii, “Self-Adjoint Elliptic Problems: Scattering Operators and Polarization on the Boundary Edges,” Algebra Analiz 6 (4), 157–186 (1994).

    MathSciNet  Google Scholar 

  34. S. A. Nazarov, “Self-adjoint Extensions of the Operator of the Dirichlet Problem in a Three-Dimensional Domain with an Edge,” Sib. Zh. Industr. Mat. 11 (1), 80–95 (2008).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Problems in Machine Science, Russian Academy of Sciences, Vasil’evskii Ostrov, Bol’shoipr. 61, St. Petersburg, 199178, Russia

    S. A. Nazarov

Authors
  1. S. A. Nazarov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. A. Nazarov.

Additional information

Original Russian Text © S.A. Nazarov, 2010, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2010, Vol. 50, No. 6, pp. 1092–1108.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nazarov, S.A. Opening gaps in the spectrum of the water-wave problem in a periodic channel. Comput. Math. and Math. Phys. 50, 1038–1054 (2010). https://doi.org/10.1134/S0965542510060102

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542510060102

Search

Navigation