Abstract
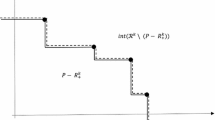
The problem of approximating the Pareto frontier (nondominated frontier) of the feasible set of criteria vectors in nonlinear multicriteria optimization problems is considered. The problem is solved by approximating the Edgeworth-Pareto hull (EPH), i.e., the maximum set with the same Pareto frontier as the original feasible set of criteria vectors. An EPH approximation method is studied that is based on the statistical accuracy estimation of the current approximation and on adaptive supplement of a metric net whose EPH approximates the desired set. The convergence of the method is proved, estimates for the convergence rate are obtained, and the efficiency of the method is studied in the case of a compact feasible set and continuous criteria functions. It is shown that the convergence rate of the method with respect to the number k of iterations is no lower than \( o\left( {k^{{1 \mathord{\left/ {\vphantom {1 {\overline {dm} Y}}} \right. \kern-\nulldelimiterspace} {\overline {dm} Y}}} } \right) \), where \( \overline {dm} Y \) is the upper metric dimension of the feasible set of criteria vectors.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
P. S. Krasnoshchekov, V. V. Morozov, and V. V. Fedorov, “Decomposition in Projection Problems,” Izv. Akad. Nauk, Ser. Tekh. Kibern., No. 2, 7–17 (1979).
Yu. G. Evtushenko and M. A. Potapov, “Numerical Methods for Multicriteria Problems,” Dokl. Akad. Nauk SSSR 291, 25–29 (1986).
R. Shtoier, Multiple Criteria Optimization: Theory, Computations, and Applications (Wiley, New York, 1986; Radio i Svyaz’, Moscow, 1992).
A. V. Lotov, V. A. Bushenkov, G. K. Kamenev, and O. L. Chernykh, Computer and Search for Balanced Tradeoff: The Feasible Goals Method (Nauka, Moscow, 1997) [in Russian].
K. Miettinen, Nonlinear Multiobjective Optimization (Kluwer, Boston, 1999).
A. V. Lotov, V. Bushenkov, and G. Kamenev, Feasible Goals Method: Search for Smart Decisions (Computing Center of the RAS, Moscow, 2001).
A. V. Lotov, V. Bushenkov, and G. K. Kamenev, Interactive Decision Maps: Approximation and Visualization of Pareto Frontier (Kluwer, Boston, 2004).
A. V. Lotov and I. I. Pospelova, Multicriteria Decision Making Problems (Maks, Moscow, 2008) [in Russian].
G. K. Kamenev, Optimal Adaptive Methods for Polyhedral Approximation of Convex Bodies (Vychisl. Tsentr Ross. Akad. Nauk, Moscow, 2007) [in Russian].
V. E. Berezkin, G. K. Kamenev, and A. V. Lotov, “Hybrid Adaptive Methods for Approximating a Nonconvex Multidimensional Pareto Frontier,” Zh. Vychisl. Mat. Mat. Fiz. 46, 2009–2023 (2006) [Comput. Math. Math. Phys. 46, 1918–1931 (2006)].
G. K. Kamenev and D. L. Kondrat’ev, “One Research Technique for Nonclosed Nonlinear Models,” Mat. Model., No. 3, 105–118 (1992).
G. K. Kamenev, “Approximation of Completely Bounded Sets by the Deep Holes Method,” Zh. Vychisl. Mat. Mat. Fiz. 41, 1751–1760 (2001) [Comput. Math. Math. Phys. 41, 1667–1675 (2001)].
A. N. Shiryaev, Probability (Nauka, Moscow, 1980) [in Russian].
A. N. Kolmogorov and V. M. Tikhomirov, “E-Entropy and ε-Capacity of Sets in Function Spaces,” Usp. Mat. Nauk 14(2), 3–86 (1959).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © G.K. Kamenev, 2009, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2009, Vol. 49, No. 12, pp. 2103–2113.
Rights and permissions
About this article
Cite this article
Kamenev, G.K. Study of an adaptive single-phase method for approximating the multidimensional Pareto frontier in nonlinear systems. Comput. Math. and Math. Phys. 49, 2006–2016 (2009). https://doi.org/10.1134/S0965542509120021
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0965542509120021