Skip to main content
SpringerLink
Log in

Concerning the features of deformation of a compliant coating by pressure pulsations in a turbulent boundary layer

  • Published:
Thermophysics and Aeromechanics Aims and scope

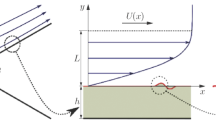
Abstract

Deformations of a compliant coating in a turbulent flow, measured previously and calculated in this work, are compared. The calculated spectral density of coating deformations at low frequencies (25–250 Hz) turned out to be almost two orders of magnitude higher than the measured one, and the rms value of the measured deformation was seven times lower than the calculated one. The transitional regime for stabilizing the forced coating oscillations under the action of a pressure wave is calculated. It is shown that the coating almost always works in the transition regime, without reaching the maximum deformation amplitudes that are characteristic of the steady state. It is concluded that it is necessary to use more complex boundary conditions that take into account the non-stationary character of the process because the amplitude of coating deformation varies in a complex way during the lifetime of organized structures moving in a turbulent boundary layer.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D.M. Bushnell, J.N. Hefner, and R.L. Ash, Effect of compliant wall motion on turbulent boundary layers, Phys. Fluids, 1977, Vol. 20, P. S31–S48.

    Article  ADS  Google Scholar 

  2. J.J. Riley, M. Gad-el-Hak, and R.W. Metcalfe, Compliant coatings, Ann. Rev. Fluid Mech., 1988, Vol. 20, P. 393–420.

    Article  ADS  Google Scholar 

  3. M. Gad-el-Hak, Drag reduction using compliant walls. Flow past highly compliant boundaries and in collapsible tubes, in: P.W. Carpenter, T.J. Pedley (Eds.), Fluid Mechanics and its Applications, 2003, Vol. 72, P. 191–229.

    Article  MathSciNet  Google Scholar 

  4. P.W. Carpenter and A.D. Garrad, The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part I. Tollmien-Schlichting instabilities, J. Fluid Mech., 1985, Vol. 155, P. 465–510.

    Article  ADS  Google Scholar 

  5. P.W. Carpenter and A.D. Garrad, The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part II. Flow-induced surface instabilities, J. Fluid Mech., 1986, Vol. 170, P. 199–232.

    Article  ADS  Google Scholar 

  6. K.S. Yeo, H.Z. Zhao, and B.C. Khoo, Turbulent boundary layer over a compliant surface — absolute and convective, J. Fluid Mech., 2001, Vol. 449, P. 141–168.

    Article  ADS  Google Scholar 

  7. T. Endo and R. Himeno, Direct numerical simulation of turbulent flow over a compliant surface, J. Turbulence, 2002, Vol. 3, P. 007–1–007–10.

    Article  ADS  Google Scholar 

  8. S. Xu, D. Rempfer, and J. Lumley, Turbulence over compliant surface: numerical simulation and analysis, J. Fluid Mech., 2003, Vol. 478, P. 11–34.

    Article  ADS  MathSciNet  Google Scholar 

  9. E. Kim and H. Choi, Space-time characteristics of a compliant wall in a turbulent channel flow, J. Fluid Mech., 2014, Vol. 756, P. 30–53.

    Article  ADS  MathSciNet  Google Scholar 

  10. M. Luhar, A.S. Sharma, and B.J. McKeon, A framework for studying the effect of compliant surfaces on wall turbulence, J. Fluid Mech., 2015, Vol. 768, P. 415–441.

    Article  ADS  MathSciNet  Google Scholar 

  11. M. Gad-el-Hak, The response of elastic and viscoelastic surfaces to a turbulent boundary layer, Trans. ASME J. Appl. Mech., 1986, Vol. 53, P. 206–212.

    Article  ADS  Google Scholar 

  12. D.E. Hess, R.A. Peattie, and W.H. Schwarz, A noninvasive method for the measurement of flow-induced surface displacement of a compliant surface, Exp. Fluids, 1993, Vol. 14, P. 78–84.

    Article  Google Scholar 

  13. P. Castellinu, M. Martarelli, and E.P. Tomasini, Laser Doppler vibrometry: development of advanced solutions answering to technology’s needs, Mech. Syst. Signal Process, 2006, Vol. 20, P. 1265–1285.

    Article  ADS  Google Scholar 

  14. T. Lee, M. Fisher, and W.H. Schwarz, The measurement of flow-induced surface displacement on a compliant surface by optical holographic interferometry, Exp. Fluids, 1993, Vol. 14, P. 159–168.

    Article  Google Scholar 

  15. C. Zhang, R. Miorini, and J. Katz, Integrating Mach-Zehnder interferometry with TPIV to measure the time-resolved deformation of a compliant wall along with the 3D velocity field in a turbulent channel flow, Exp. Fluids, 2015, Vol. 56, Iss. 11, P. 203–1–203–22.

    Article  Google Scholar 

  16. H.O.G. Benschop, A.J. Greidanus, R. Delfos, J. Westrweel, and W.-P. Breugem, Deformation of a linear viscoelastic compliant coating in a turbulent flow, J. Fluid Mech., 2019, Vol. 859, P. 613–658.

    Article  ADS  MathSciNet  Google Scholar 

  17. C. Zhang, J. Wang, W. Blake, and J. Katz, Deformation of a compliant wall in a turbulent channel flow, J. Fluid Mech., 2017, Vol. 823, P. 345–390.

    Article  ADS  MathSciNet  Google Scholar 

  18. V.M. Kulik, B.N. Semenov, A.V. Boiko, B. Seoudi, H.H. Chun, and I. Lee, Measurement of dynamic properties of viscoelastic materials, Experimental Mechanics, 2009, Vol. 49, P. 417–425.

    Article  Google Scholar 

  19. A.V. Boiko, V.M. Kulik, B. Seoudi, H.H. Chun, and I. Lee, Measurement method of complex viscoelastic material properties, Int. J. Solids and Structures, 2010, Vol. 47, No. 3–4, P. 374–382.

    Article  Google Scholar 

  20. V.M. Kulik, Forced oscillations of a layer of viscoelastic material under the action of a convective pressure wave, J. Appl. Mech. Tech. Phys., 2007, Vol. 48, P. 221–228.

    Article  ADS  Google Scholar 

  21. V.M. Kulik, Action of a turbulent flow on a hard compliant coating, Int. J. Heat and Fluid Flow, 2012, Vol. 33, P. 232–241.

    Article  MathSciNet  Google Scholar 

  22. P.R. Bandyopadhyay, C. Henoch, J.D. Hrubes, B.N. Semenov, A.I. Amirov, V.M. Kulik, A.G. Malyuga, K.-S. Choi, and M.P. Escudier, Experiments on the effects of aging on compliant coating drag reduction, Phys. Fluids, 2005, Vol. 17, No. 8, P. 085104-1–085104-9.

    Article  ADS  Google Scholar 

  23. V.M. Kulik, Aging of pliable coatings, J. Eng. Phys. Thermoph., 2000, Vol. 73, No. 5, P. 1065–1068.

    Article  Google Scholar 

  24. L.D. Landau and E.M. Lifshitz, Theory of Elasticity, 3rd Ed., Pergamon Press, Oxford, New York, 1986.

    MATH  Google Scholar 

  25. Yu.G. Blyudze and O.N. Dokuchaev, Measurements of velocity and pressure pulsations in turbulent boundary layers, Fluid Dynamics, 1969, No. 5, P. 118–122.

  26. V.M. Kulik, Deformation of viscoelastic coating in a turbulent flow, Thermophysics and Aeromechanics, 2009, Vol. 16, No. 1, P. 43–55.

    Article  ADS  Google Scholar 

  27. T.B. Benjamin, Effects of a flexible boundary on hydrodynamic stability, J. Fluid Mech., 1960, Vol. 9, P. 513–532.

    Article  ADS  MathSciNet  Google Scholar 

  28. M.T. Landahl, On the stability of laminar incompressible boundary layer over a flexible surface, J. Fluid Mech., 1962, Vol. 13, P. 609–632.

    Article  ADS  Google Scholar 

  29. B.N. Semenov, Analysis of deformation characteristics of viscoelastic coatings, Hydrodynamics and acoustics of the wall and free flows, IT SO AN SSSR, Novosibirsk, 1981, P. 57–76.

    Google Scholar 

  30. V.M. Kulik and S.L. Morozova, Response of a compliant coating to turbulent pressure pulsations, Thermophysics and Aeromechanics, 2001, Vol. 8, No 1, P. 55–70.

    Google Scholar 

  31. W.W. Willmarth, Structure of turbulence in boundary layers, Adv. Appl. Mech., 1975, Vol. 15, P. 159–254.

    Article  ADS  Google Scholar 

  32. G. Schewe, On the structure and resolution of wall-pressure fluctuations associated with turbulent boundary-layer flow, J. Fluid Mech., 1983, Vol. 134, P. 311–328.

    Article  ADS  Google Scholar 

  33. S.J. Russel, Measured wall pressure signatures of turbulence producing structures, Proc. Intern. Symp. Seawater Drag Reduction, Newport, RI, 1998, P. 63–71.

    Google Scholar 

  34. V.M. Kulik, I.S. Poguda, and B.N. Semenov, Experimental investigation of one-layer viscoelastic coatings action on turbulent friction and wall pressure pulsations, Recent Developments in Turbulence Management, Ed. K.-S. Choi, Kluwer, Dordrecht, 1991, P. 263–289.

    Chapter  Google Scholar 

  35. J.H. Duncan, The response of an incompressible, viscoelastic coating to pressure fluctuations in a turbulent boundary layer, J. Fluid Mech., 1986, Vol. 171, P. 339–363.

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kutateladze Institute of Thermophysics SB RAS, Novosibirsk, Russia

    V. M. Kulik

Authors
  1. V. M. Kulik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. M. Kulik.

Additional information

The work was carried out on the theme No. 20.1.3, section III of the Program of fundamental scientific research of state Academies for 2017–2020.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kulik, V.M. Concerning the features of deformation of a compliant coating by pressure pulsations in a turbulent boundary layer. Thermophys. Aeromech. 27, 71–80 (2020). https://doi.org/10.1134/S0869864320010060

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0869864320010060

Keywords

Search

Navigation