Skip to main content
SpringerLink
Log in

Symbolic calculations in studying the problem of three bodies with variable masses

  • Published:
Programming and Computer Software Aims and scope Submit manuscript

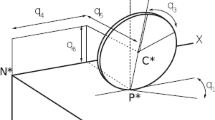
Abstract

The classical problem of three bodies with variable masses is considered in the case when the masses of all three bodies vary isotropically. Solutions to the equation of motion in terms of the osculating elements of the aperiodic quasi-conical motion and the secular perturbations of the orbital elements of the system are examined. An algorithm for calculating the secular part of the perturbing functions and derivation of the differential equations determining the secular perturbations of the orbital elements are discussed. All the relevant symbolic calculations are carried out using the Mathematica computer algebra system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Roy, A.E., Orbital Motion, Bristol: Hilger, 1978.

    MATH  Google Scholar 

  2. Bekov, A.A. and Omarov, T.B., The theory of orbits in non-stationary stellar systems, Astron. Astrophys. Trans., 2003, vol. 22, no. 2, pp. 145–153.

    Article  Google Scholar 

  3. Minglibaev, M.D., Dinamika gravitiruyushchikh tel s peremennymi massami i razmerami (Dynamics of Gravitating Bodies of Variable Masses and Sizes), Lambert Academic, 2012.

    Google Scholar 

  4. Radzievskii, V.V. and Gel’fgat, B.E., The restricted problem of two bodies of variable mass, Astron. Zh., 1957, vol. 34, no. 4, pp. 581–587.

    Google Scholar 

  5. Berković, L.M., Gylden-Meščerski problem, Celestial Mech., 1981, vol. 24, pp. 407–429.

    Article  MathSciNet  Google Scholar 

  6. Rahoma, W.A, Abd El-Salam, F.A., and Ahmed, M.K., Analytical treatment of the two body problem with slowly varying mass, J. Astrophys. Astron., 2009, vol. 30, no. 3–4, pp. 187–205.

    Article  Google Scholar 

  7. Singh, J. and Ishwar, B., Effect of perturbations on the location of equilibrium points in the restricted problem of three bodies with variable mass, Celestial Mech., 1984, vol. 32, pp. 297–305.

    Article  MATH  MathSciNet  Google Scholar 

  8. Luk’yanov, L.G., On partial solutions in the restricted three body problem with arbitrary varying masses, Astron. Zh., 1989, vol. 66, no. 2, pp. 385–392.

    MATH  MathSciNet  Google Scholar 

  9. Brumberg, V.A., Analiticheskie algoritmy v nebesnoi mekhanike (Analytical Techniques of Celestial Mechanics), Moscow: Nauka, 1980.

    Google Scholar 

  10. Wolfram, S., The Mathematica Book, New York: Wolfram Media, 1999, 4th ed.

    MATH  Google Scholar 

  11. Prokopenya, A.N., Reshenie fizicheskikh zadach s ispol’zovaniem sistemy Mathematica (Solving Physical Problems Using Mathematica Computer Algebra System), Brest: Brest Gos. Tekhn. Univ., 2005.

    Google Scholar 

  12. Charlier, C.L., Die Mechanik des Himmels, Berlin: 1927.

    MATH  Google Scholar 

  13. Markeev, A.P., Teoreticheskaya mekhanika (Theoretical Mechanics), Izhevsk: NITs RDKh, 2001.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Warsaw University of Life Sciences, ul. Novoursynovska 159, Warsaw, 02-776, Poland

    A. N. Prokopenya

  2. Innovation High School Collegium of Mazovia, ul. Sokolowska 161, Siedlce, 08-110, Poland

    A. N. Prokopenya

  3. Al-Farabi Kazakh National University, pr. al-Farabi 71, Almaty, 050040, Kazakhstan

    M. Zh. Minglibayev & G. M. Mayemerova

  4. Fesenkov Astrophysical Institute, Observatoriya 23, Almaty, 050020, Kazakhstan

    M. Zh. Minglibayev

Authors
  1. A. N. Prokopenya
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Zh. Minglibayev
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. M. Mayemerova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. N. Prokopenya.

Additional information

Original Russian Text © A.N. Prokopenya, M.Zh. Minglibayev, G.M. Mayemerova, 2014, published in Programmirovanie, 2014, Vol. 40, No. 2.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Prokopenya, A.N., Minglibayev, M.Z. & Mayemerova, G.M. Symbolic calculations in studying the problem of three bodies with variable masses. Program Comput Soft 40, 79–85 (2014). https://doi.org/10.1134/S036176881402008X

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S036176881402008X

Keywords

Search

Navigation