Skip to main content
SpringerLink
Log in

Solving the Problem of Groundwater Flow in an Inundated Massif with Vertical Drains

  • HYDROPHYSICAL PROCESSES
  • Published:
Water Resources Aims and scope Submit manuscript

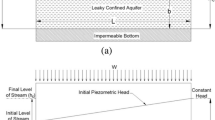
Abstract

The earlier solutions of the problem of groundwater flow in an inundated rock massif with vertically drains (drain trenches) are represented by extremely complex mathematical relationships in complex variables which make them difficult to use in applied problems. A new approximate-hydromechanical solution of the problem was obtained with the use of velocity hodograph and the presentation of model relationships in elementary functions, which coincides with the exact data in boundary points and which are in almost complete agreement (⪡1%) with the results of exact calculations by V.V. Vedernikov for special cases. For the first time, a picture of the field of full flow velocities was analytically constructed in the form of an isotach family for the given inundated massif with drains, showing the heterogeneous character of velocity distribution in it at the presence of water in the drain. Groundwater flow diagrams are also presented for boundary lines (in particular, in comparison with the case when there is no water in the drain), along with plots of flow functions and heads.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.

Similar content being viewed by others

REFERENCES

  1. Anakhaev, K.N., On determining elliptic Jacobi functions, Vestn. RUDN. Ser. Matem., Inform., Fizika. 2009, no. 2, pp. 90–95.

  2. Anakhaev, K.N., The calculation of potential flows, Dokl. Akad. Nauk, 2005, vol. 401, no. 3, pp. 337–341.

    Google Scholar 

  3. Anakhaev, K.N., A rigorous solution of the problem of free filtration from watercourses by semi-inverse method, Prikl. Gidromekh., Kiev, 2008, vol. 10 (82), no. 1, pp. 80–85.

  4. Bronshtein, I.N. and Semendyaev, K.A., Spravochnik po matematike (Reference Book on Mathematics), Moscow: Nauka, 1980.

  5. Vedernikov, V.V., Teoriya fil’tratsii i ee primenenie v oblasti irrigatsii i drenazha (Theory of Flow in Porous Media and Its Application to Irrigation and Drainage), Moscow; Leningrad: Gosstroiizdat, 1939.

  6. Dvait, G.B., Tablitsy integralov i drugie matematicheskie formuly (Tables of Integrals and Other Mathematical Formulas), Moscow: Nauka, 1977.

  7. Lavrik, V.I. and Savenkov, V.N., Spravochnik po konformnym otobrazheniyam (Reference Book on Conformal Transformations), Kiev: Nauk. dumka, 1970.

  8. Miln-Tomson, L., Elliptic integrals, Spravochnik po spetsial’nym funktsiyam (Reference Book on Special Functions), Abramovits, M. and Stigan, I., Eds., Moscow: Nauka, 1979, pp. 401–441.

    Google Scholar 

  9. Miln-Thomson, L., Elliptic functions Jacobi theta-function, Spravochnik po spetsial’nym funktsiyam (Reference Book on Special Functions), Abramovits, M. and Stigan, I., Eds., Moscow: Nauka, 1979, pp. 380–440.

    Google Scholar 

  10. Nel’son-Skornyakov, F.B., Fil’tratsiya v odnorodnoi srede (Water Flow in a Homogeneous Medium), Moscow: Sovetskaya nauka, 1949.

  11. Pavlovskii, N.N. Sobranie sochinenii (Collected Works), vol. 2, Dvizhenie gruntovykh vod (Subsoil Water Motion), Moscow; Leningrad: Izd. AN SSSR, 1956.

  12. Fil’chakov, P.F., Spravochnik po vysshei matematike (Reference Book on Higher Mathematics), Kiev.: Nauk. dumka, 1973.

  13. Anakhaev, K.N., A contribution to calculation of the mathematical pendulum, Doklady Physics, 2014, vol. 59, no. 11, pp. 528–533.

    Article  Google Scholar 

  14. Anakhaev, K.N., Calculation of free seepage from watercourses with curvilinear profiles, Water Resour., 2007, vol. 34, no. 3, pp. 295–300.

    Article  Google Scholar 

  15. Donat, J., Die Wirkung der Dranungen, Wasserkraft und Wasserwirtschaft, 1936, no. 31, pp. 90–94.

Download references

Funding

The study was carried out under the subjects of Governmental Orders to IAMA KBSC RAS (122041800015-8) and WPI RAS (FMWZ-2022-0001).

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics and Automation, Kabardin-Balkar Scientific Center, Russian Academy of Sciences (IAMA KBSC RAS), 360000, Nal’chik, KBR, Russia

    K. N. Anakhaev

  2. Water Problems Institute, Russian Academy of Sciences (WPI RAS), 119333, Moscow, Russia

    K. N. Anakhaev, V. V. Belikov & N. M. Borisova

  3. Russian University of Transport (RUT (MIIT)), 127994, Moscow, Russia

    Kh. K. Anakhaeva

Authors
  1. K. N. Anakhaev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. V. Belikov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kh. K. Anakhaeva
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. N. M. Borisova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. M. Borisova.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Anakhaev, K.N., Belikov, V.V., Anakhaeva, K.K. et al. Solving the Problem of Groundwater Flow in an Inundated Massif with Vertical Drains. Water Resour 50, 392–399 (2023). https://doi.org/10.1134/S0097807823030028

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0097807823030028

Keywords:

Search

Navigation