Skip to main content
SpringerLink
Log in

On Graphs in Which Neighborhoods of Vertices Are Strongly Regular with Parameters (85,14,3,2) or (325,54,3,10)

  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

Abstract

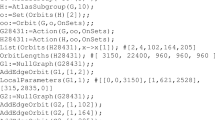
J. Koolen posed the problem of studying distance-regular graphs in which neighborhoods of vertices are strongly regular graphs with nonprincipal eigenvalue at most t for a given positive integer t. This problem was solved earlier for t = 3. In the case t = 4, the problem was reduced to studying graphs in which neighborhoods of vertices have parameters (352,26,0,2), (352,36,0,4), (243,22,1,2), (729,112,1,20), (204,28,2,4), (232,33,2,5), (676,108,2,20), (85,14,3,2), or (325,54,3,10). In the present paper, we prove that a distance-regular graph in which neighborhoods of vertices are strongly regular with parameters (85, 14, 3, 2) or (325, 54, 3, 10) has intersection array {85, 70, 1; 1, 14, 85} or {325, 270, 1; 1, 54, 325}. In addition, we find possible automorphisms of a graph with intersection array {85, 70, 1; 1, 14, 85}.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. A. Makhnev and D. V. Paduchikh, “Distance regular graphs in which local subgraphs are strongly regular graphs with the second eigenvalue at most 3,” Dokl. Math. 92 (2), 568–571 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  2. A. A. Makhnev, “Strongly regular graphs with nonprincipal eigenvalue 4 and their extensions,” Izv. Gomel. Gos. Univ. 84 (3), 84–85 (2014).

    MathSciNet  Google Scholar 

  3. A. A. Makhnev and D. V. Paduchikh, “On extensions of strongly regular graphs with eigenvalue 4,” Trudy Inst. Mat. Mekh. UrO RAN 21 (3), 233–255 (2015).

    MathSciNet  MATH  Google Scholar 

  4. A. A. Makhnev and D. V. Paduchikh, “An automorphism group of a distance-regular graph with intersection array {24, 21, 3; 1, 3, 18},” Algebra Logic 51 (4), 319–332 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  5. A. L. Gavrilyuk and A. A. Makhnev, “On automorphisms of distance-regular graphs with intersection array {56, 45, 1; 1, 9, 56},” Dokl. Math. 81 (3), 439–442 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  6. D. V. Paduchikh, “On the automorphisms of the strongly regular graph with parameters (85,14,3,2),” Discrete Math. Appl. 19 (1), 89–111 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  7. A. V. Zavarnitsine, “Finite simple groups with narrow prime spectrum,” Sib. Electron. Math. Rep. 6, 1–12 (2009).

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kabardino-Balkarian State University, Nalchik, Kabardino-Balkar Republic, 360004, Russia

    M. M. Isakova & A. A. Tokbaeva

  2. Krasovskii Institute of Mathematics and Mechanics, Ural Branch of the Russian Academy of Sciences, Yekaterinburg, 620990, Russia

    A. A. Makhnev

  3. Ural Federal University, Yekaterinburg, 620002, Russia

    A. A. Makhnev

Authors
  1. M. M. Isakova
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. A. Makhnev
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. A. Tokbaeva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. M. Isakova.

Additional information

Original Russian Text © M.M. Isakova, A.A.Makhnev, A.A. Tokbaeva, 2016, published in Trudy Instituta Matematiki i Mekhaniki UrO RAN, 2016, Vol. 22, No. 3.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Isakova, M.M., Makhnev, A.A. & Tokbaeva, A.A. On Graphs in Which Neighborhoods of Vertices Are Strongly Regular with Parameters (85,14,3,2) or (325,54,3,10). Proc. Steklov Inst. Math. 299 (Suppl 1), 68–74 (2017). https://doi.org/10.1134/S0081543817090097

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543817090097

Keywords

Search

Navigation