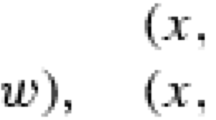Skip to main content
SpringerLink
Log in

Plane rational quartics and K3 surfaces

  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

Abstract

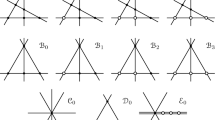
We study actions of the symmetric group S4 on K3 surfaces X that satisfy the following condition: there exists an equivariant birational contraction \(\bar r:X \to \bar X\) to a K3 surface \(\bar X\) with ADE singularities such that the quotient space \(\bar X\) /S4 is isomorphic to P2. We prove that up to smooth equivariant deformations there exist exactly 15 such actions of the group S4 on K3 surfaces, and that these actions are realized as actions of the Galois groups on the Galoisations \(\bar X\) of the dualizing coverings of the plane which are associated with plane rational quartics without A 4, A 6, and E 6 singularities as their singular points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. Ballico and A. Hefez, “On the Galois group associated to a generically étale morphism, ” Commun. Algebra 14 (5), 899–909 (1986).

    Article  MathSciNet  MATH  Google Scholar 

  2. H. Cartan, “Quotient d’un espace analytique par un groupe d’automorphismes, ” in Algebraic Geometry and Topology: A Symposium in Honor of S. Lefschetz, Princeton, 1954 (Princeton Univ. Press, Princeton, NJ, 1957), pp. 90–102.

    Google Scholar 

  3. F. Catanese, “Automorphisms of rational double points and moduli spaces of surfaces of general type, ” Compos. Math. 61 (1), 81–102 (1987).

    MathSciNet  MATH  Google Scholar 

  4. Vik. S. Kulikov, “Hurwitz curves, ” Usp. Mat. Nauk 62 (6), 3–86 (2007) [Russ. Math. Surv. 62, 1043–1119 (2007)].

    Article  MathSciNet  MATH  Google Scholar 

  5. Vik. S. Kulikov, “A remark on classical Pluecker’s formulae,” arXiv: 1101.5042 [math.AG].

  6. Vik. S. Kulikov, “Dualizing coverings of the plane, ” Izv. Ross. Akad. Nauk, Ser. Mat. 79 (5), 163–192 (2015) [Izv. Mat. 79, 1013–1042 (2015)].

    Article  MathSciNet  Google Scholar 

  7. D. Mumford, “The topology of normal singularities of an algebraic surface and a criterion for simplicity, ” Publ. Math., Inst. Hautes Étud. Sci. 9, 5–22 (1961).

    Article  MathSciNet  MATH  Google Scholar 

  8. S. Nakano, “On the inverse of monoidal transformation, ” Publ. Res. Inst. Math. Sci., Kyoto Univ. 6 (3), 483–502 (1971).

    Article  MathSciNet  MATH  Google Scholar 

  9. V. V. Nikulin, “Finite automorphism groups of Kähler K3 surfaces, ” Tr. Mosk. Mat. Obshch. 38, 75–137 (1979) [Trans. Moscow Math. Soc. 2, 71–135 (1980)].

    MathSciNet  MATH  Google Scholar 

  10. V. V. Nikulin, “Degenerations of Kählerian K3 surfaces with finite symplectic automorphism groups, ” Izv. Ross. Akad. Nauk, Ser. Mat. 79 (4), 103–158 (2015) [Izv. Mat. 79, 740–794 (2015)].

    Article  MathSciNet  MATH  Google Scholar 

  11. I. R. Shafarevich et al., AlgebraicSurfaces (Nauka, Moscow, 1965), Tr. Mat. Inst. im. V.A. Steklova, Akad. Nauk SSSR 75 [Proc. Steklov Inst. Math. 75 (1967)].

    Google Scholar 

  12. G. C. Shephard and J. A. Todd, “Finite unitary reflection groups, ” Can. J. Math. 6, 274–304 (1954).

    Article  MathSciNet  MATH  Google Scholar 

  13. K. Stein, “Analytische Zerlegungen komplexer Räume, ” Math. Ann. 132, 63–93 (1956).

    Article  MathSciNet  MATH  Google Scholar 

  14. J. M. Wahl, “Equisingular deformations of plane algebroid curves, ” Trans. Am. Math. Soc. 193, 143–170 (1974).

    Article  MathSciNet  MATH  Google Scholar 

  15. C. T. C. Wall, “Duality of singular plane curves, ” J. London Math. Soc., Ser.2, 50 (2), 265–275 (1994).

    Article  MathSciNet  MATH  Google Scholar 

  16. C. T. C. Wall, “Geometry of quartic curves, ” Math. Proc. Cambridge Philos. Soc. 117 (3), 415–423 (1995).

    Article  MathSciNet  MATH  Google Scholar 

  17. U. Whitcher, “Symplectic automorphisms and Picard group of a K3 surface, ” Commun. Algebra 39 (4), 1427–1440 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  18. G. Xiao, “Galois covers between K3 surfaces, ” Ann. Inst. Fourier 46 (1), 73–88 (1996).

    Article  MathSciNet  MATH  Google Scholar 

  19. O. Zariski, “Studies in equisingularity. I: Equivalent singularities of plane algebroid curves, ” Am. J. Math. 87, 507–536 (1965).

    Article  MathSciNet  MATH  Google Scholar 

  20. O. Zariski, “Studies in equisingularity. II: Equisingularity in codimension 1 (and characteristic zero), ” Am. J. Math. 87, 972–1006 (1965).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Steklov Mathematical Institute of Russian Academy of Sciences, ul. Gubkina 8, Moscow, 119991, Russia

    Vik. S. Kulikov

Authors
  1. Vik. S. Kulikov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vik. S. Kulikov.

Additional information

Original Russian Text © Vik.S. Kulikov, 2016, published in Trudy Matematicheskogo Instituta imeni V.A. Steklova, 2016, Vol. 294, pp. 105–140.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kulikov, V.S. Plane rational quartics and K3 surfaces. Proc. Steklov Inst. Math. 294, 95–128 (2016). https://doi.org/10.1134/S0081543816060079

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543816060079

Search

Navigation