Skip to main content
SpringerLink
Log in

Coupled-mode flutter of an elastic plate in a gas flow with a boundary layer

  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

Abstract

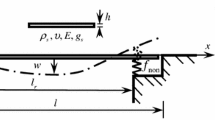
The stability of an elastic plate in a supersonic gas flow is considered in the presence of a boundary layer formed on the surface of the plate. The problem is solved in two statements. In the first statement, the plate is of large but finite length, and a coupled-mode type of flutter is examined (the effect of the boundary layer on another, single-mode, type of flutter has been studied earlier). In the second statement, the plate is assumed to be infinite, and the character of its instability (absolute or convective) is analyzed. In both cases, the instability is determined by a branch point of the roots of the dispersion equation, and the mathematical analysis is the same. It is proved that instability in a uniform gas flow is weakened by a boundary layer but cannot be suppressed completely, while in the case of a stable plate in a uniform flow the boundary layer leads to the destabilization of the plate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P. W. Carpenter and A. D. Garrad, “The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1: Tollmien-Schlichting instabilities,” J. Fluid Mech. 155, 465–510 (1985).

    Article  MATH  Google Scholar 

  2. P. W. Carpenter and A. D. Garrad, “The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 2: Flow-induced surface instabilities,” J. Fluid Mech. 170, 199–232 (1986).

    Article  MATH  Google Scholar 

  3. I. V. Savenkov, “The suppression of the growth of nonlinear wave packets by the elasticity of the surface around which flow occurs,” Zh. Vychisl. Mat. Mat. Fiz. 35(1), 95–103 (1995) [Comput. Math. Math. Phys. 35, 73–79 (1995)].

    MathSciNet  Google Scholar 

  4. O. Wiplier and U. Ehrenstein, “On the absolute instability in a boundary-layer flow with compliant coatings,” Eur. J. Mech. B: Fluids 20(1), 127–144 (2001).

    Article  Google Scholar 

  5. J. Miles, “Stability of inviscid shear flow over a flexible boundary,” J. Fluid Mech. 434, 371–378 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  6. V. V. Vedeneev, “Flutter of a wide strip plate in a supersonic gas flow,” Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 5, 155–169 (2005) [Fluid Dyn. 40, 805–817 (2005)].

    Google Scholar 

  7. A. G. Kulikovskii, “On the stability of homogeneous states,” Prikl. Mat. Mekh. 30(1), 148–153 (1966) [J. Appl. Math. Mech. 30, 180–187 (1966)].

    Google Scholar 

  8. A. G. Kulikovskii, “The global instability of uniform flows in non-one-dimensional regions,” Prikl. Mat. Mekh. vn70(2), 257–263 (2006) [J. Appl. Math. Mech. 70, 229–234 (2006)].

    MathSciNet  Google Scholar 

  9. V. V. Vedeneev, “Panel flutter at low supersonic speeds,” J. Fluids Struct. 29, 79–96 (2012).

    Article  Google Scholar 

  10. V. V. Vedeneev, S. V. Guvernyuk, A. F. Zubkov, and M. E. Kolotnikov, “Experimental investigation of single-mode panel flutter in supersonic gas flow,” Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 2, 161–175 (2010) [Fluid Dyn. 45, 312–324 (2010)].

    Google Scholar 

  11. E. H. Dowell, “Generalized aerodynamic forces on a flexible plate undergoing transient motion in a shear flow with an application to panel flutter,” AIAA J. 9(5), 834–841 (1971).

    Article  Google Scholar 

  12. E. H. Dowell, “Aerodynamic boundary layer effects on flutter and damping of plates,” J. Aircr. 10(12), 734–738 (1973).

    Article  Google Scholar 

  13. A. Hashimoto, T. Aoyama, and Y. Nakamura, “Effects of turbulent boundary layer on panel flutter,” AIAA J. 47(12), 2785–2791 (2009).

    Article  Google Scholar 

  14. L. Muhlstein, Jr., P. A. Gaspers, Jr., and D. W. Riddle, “An experimental study of the influence of the turbulent boundary layer on panel flutter,” NASA TN D-4486 (Ames Res. Center, NASA, Moffett Field, CA, 1968).

    Google Scholar 

  15. P. A. Gaspers, Jr., L. Muhlstein, Jr., and D. N. Petroff, “Further results on the influence of the turbulent boundary layer on panel flutter,” NASA TN D-5798 (Ames Res. Center, NASA, Moffett Field, CA, 1970).

    Google Scholar 

  16. V. V. Vedeneev, “Single-mode plate flutter taking the boundary layer into account,” Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, No. 3, 147–160 (2012) [Fluid Dyn. 47, 417–429 (2012)].

    Google Scholar 

  17. S. A. Gaponov and A. A. Maslov, Development of Perturbations in Compressible Flows (Nauka, Novosibirsk, 1980) [in Russian].

    Google Scholar 

  18. P. G. Drazin and W. H. Reid, Hydrodynamic Stability (Cambridge Univ. Press, Cambridge, 2004).

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mechanics and Mathematics, Moscow State University, Moscow, 119991, Russia

    V. V. Vedeneev

Authors
  1. V. V. Vedeneev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Vedeneev.

Additional information

Original Russian Text © V.V. Vedeneev, 2013, published in Trudy Matematicheskogo Instituta imeni V.A. Steklova, 2013, Vol. 281, pp. 149–161.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vedeneev, V.V. Coupled-mode flutter of an elastic plate in a gas flow with a boundary layer. Proc. Steklov Inst. Math. 281, 140–152 (2013). https://doi.org/10.1134/S0081543813040123

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543813040123

Keywords

Search

Navigation