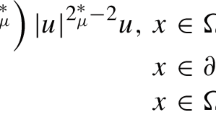Abstract
The aim of this paper is to establish sufficient conditions of the finite time blow-up in solutions of the homogeneous Dirichlet problem for the anisotropic parabolic equations with variable nonlinearity \( u_t = \sum\nolimits_{i = 1}^n {D_i (a_i (x,t)|D_i u|^{p^i (x) - 2} D_i u) + \sum\nolimits_{i = 1}^K {b_i (x,t)|u|^{\sigma _i (x,t) - 2} u} } \) . Two different cases are studied. In the first case a i ≡ a i (x), p i ≡ 2, σ i ≡ σ i (x, t), and b i (x, t) ≥ 0. We show that in this case every solution corresponding to a “large” initial function blows up in finite time if there exists at least one j for which min σ j (x, t) > 2 and either b j > 0, or b j (x, t) ≥ 0 and Σπ b −ρ(t) j (x, t) dx < ∞ with some σ(t) > 0 depending on σ j . In the case of the quasilinear equation with the exponents p i and σ i depending only on x, we show that the solutions may blow up if min σ i ≥ max p i , b i ≥ 0, and there exists at least one j for which min σ j > max p j and b j > 0. We extend these results to a semilinear equation with nonlocal forcing terms and quasilinear equations which combine the absorption (b i ≤ 0) and reaction terms.
Similar content being viewed by others
References
R. Aboulaich, D. Meskine, and A. Souissi, “New Diffusion Models in Image Processing,” Comput. Math. Appl. 56, 874–882 (2008).
E. Acerbi and G. Mingione, “Regularity Results for Stationary Electro-rheological Fluids,” Arch. Ration. Mech. Anal. 164, 213–259 (2002).
E. Acerbi, G. Mingione, and G. Seregin, “Regularity Results for Parabolic Systems Related to a Class of Non-Newtonian Fluids,” Ann. Inst. Henri Poincaré, Anal. Non Linéaire 21(1), 25–60 (2004).
Yu. A. Alkhutov, S. N. Antontsev, and V. V. Zhikov, “Parabolic Equations with Variable Order of Nonlinearity,” in Zb. Prats’ Inst. Mat., Nats. Akad. Nauk Ukr. (Inst. Mat., Nats. Akad. Nauk Ukr., Kyiv, 2009), Vol. 6 (1), pp. 23–50 [in Russian].
S. Antontsev, M. Chipot, and Y. Xie, “Uniqueness Results for Equations of the p(x)-Laplacian Type,” Adv. Math. Sci. Appl. 17, 287–304 (2007).
S. N. Antontsev and J. F. Rodrigues, “On Stationary Thermo-rheological Viscous Flows,” Ann. Univ. Ferrara, Sez. 7, Sci. Mat. 52, 19–36 (2006).
S. Antontsev and S. Shmarev, “Elliptic Equations and Systems with Nonstandard Growth Conditions: Existence, Uniqueness and Localization Properties of Solutions,” Nonlinear Anal., Theory Methods Appl. 65, 728–761 (2006).
S. Antontsev and S. Shmarev, “Elliptic Equations with Anisotropic Nonlinearity and Nonstandard Growth Conditions,” in Handbook of Differential Equations. Stationary Partial Differential Equations (Elsevier, Amsterdam, 2006), Vol. 3, pp. 1–100.
S. Antontsev and S. Shmarev, “Parabolic Equations with Anisotropic Nonstandard Growth Conditions,” in Free Boundary Problems. Theory and Applications (Birkhäuser, Basel, 2007), Int. Ser. Numer. Math. 154, pp. 33–44.
S. Antontsev and S. Shmarev, “Extinction of Solutions of Parabolic Equations with Variable Anisotropic Nonlinearities,” Tr. Mat. Inst. im. V.A. Steklova, Ross. Akad. Nauk 261, 16–25 (2008) [Proc. Steklov Inst. Math. 261, 11–21 (2008)].
S. Antontsev and S. Shmarev, “Anisotropic Parabolic Equations with Variable Nonlinearity,” Publ. Mat. 53(2), 355–399 (2009).
S. Antontsev and S. Shmarev, “Localization of Solutions of Anisotropic Parabolic Equations,” Nonlinear Anal., Theory Methods Appl. 71(12), e725–e737 (2009).
S. Antontsev and S. Shmarev, “Vanishing Solutions of Anisotropic Parabolic Equations with Variable Nonlinearity,” J. Math. Anal. Appl. 361(2), 371–391 (2010).
S. Antontsev and S. Shmarev, “Blow-up of Solutions to Parabolic Equations with Nonstandard Growth Conditions,” J. Comput. Appl. Math. 234(9), 2633–2645 (2010).
S. Antontsev and V. Zhikov, “Hihger Integrability for Parabolic Equations of p(x, t)-Laplacian Type,” Adv. Diff. Eqns. 10(9), 1053–1080 (2005).
Y. Chen, S. Levine, and M. Rao, “Variable Exponent, Linear Growth Functionals in Image Restoration,” SIAM J. Appl. Math. 66, 1383–1406 (2006).
H. Fujita, “On the Blowing up of Solutions of the Cauchy Problem for u t = Δu+u 1+α,” J. Fac. Sci. Univ. Tokyo, Sect. IA 13, 109–124 (1966).
H. Fujita, “On Some Nonexistence and Nonuniqueness Theorems for Nonlinear Parabolic Equations,” in Nonlinear Functional Analysis: Proc. Symp. Pure Math., Chicago, 1968 (Am. Math. Soc., Providence, RI, 1970), Part 1, Proc. Symp. Pure Math. 18, pp. 105–113.
V. A. Galaktionov and S. I. Pohozaev, “Blow-up and Critical Exponents for Parabolic Equations with Nondivergent Operators: Dual Porous Medium and Thin Film Operators,” J. Evol. Eqns. 6, 45–69 (2006).
V. A. Galaktionov and J. L. Vázquez, A Stability Technique for Evolution Partial Differential Equations: A Dynamical Systems Approach (Birkhäuser, Boston, 2004), Prog. Nonlinear Diff. Eqns. Appl. 56.
S. Kaplan, “On the Growth of Solutions of Quasi-linear Parabolic Equations,” Commun. Pure Appl. Math. 16, 305–330 (1963).
S. Levine, Y. Chen, and J. Stanich, “Image Restoration via Nonstandard Diffusion,” Tech. Rep. no. 04-01 (Dept. Math. Comput. Sci., Duquesne Univ., Pittsburgh, 2004).
E. Mitidieri and S. I. Pohozaev, “Nonexistence of Weak Solutions for Some Degenerate Elliptic and Parabolic Problems on ℝn,” J. Evol. Eqns. 1, 189–220 (2001).
J. P. Pinasco, “Blow-up for Parabolic and Hyperbolic Problems with Variable Exponents,” Nonlinear Anal., Theory Methods Appl. 71(3–4), 1094–1099 (2009).
S. I. Pohozaev and A. Tesei, “Blow-up of Nonnegative Solutions to Quasilinear Parabolic Inequalities,” Atti Accad. Naz. Lincei, Cl. Sci. Fis. Mat. Nat., Ser. 9, Rend. Lincei, Mat. Appl. 11(2), 99–109 (2000).
S. I. Pokhozhaev and A. Tesei, “Critical Exponents for the Absence of Solutions for Systems of Quasilinear Parabolic Inequalities,” Diff. Uravn. 37(4), 521–528 (2001) [Diff. Eqns. 37, 551–558 (2001)].
K. R. Rajagopal and M. Růžička, “Mathematical Modeling of Electrorheological Materials,” Contin. Mech. Thermodyn. 13, 59–78 (2001).
M. Růžička, Electrorheological Fluids: Modeling and Mathematical Theory (Springer, Berlin, 2000), Lect. Notes Math. 1748.
A. A. Samarskii, V. A. Galaktionov, S. P. Kurdyumov, and A. P. Mikhailov, Blow-up in Quasilinear Parabolic Equations (W. de Gruyter, Berlin, 1995).
M. Tsutsumi, “Existence and Nonexistence of Global Solutions for Nonlinear Parabolic Equations,” Publ. Res. Inst. Math. Sci., Kyoto Univ. 8, 211–229 (1972).
M. Tsutsumi, “Existence and Nonexistence of Global Solutions of the First Boundary Value Problem for a Certain Quasilinear Parabolic Equation,” Funkc. Ekvacioj 17, 13–24 (1974).
V. V. Zhikov, “On Lavrentiev’s Effect,” Dokl. Akad. Nauk 345(1), 10–14 (1995) [Dokl. Math. 52 (3), 325–329 (1995)].
V. V. Zhikov, “On Lavrentiev’s Phenomenon,” Russ. J. Math. Phys. 3(2), 249–269 (1995).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Antontsev, S., Shmarev, S. On the blow-up of solutions to anisotropic parabolic equations with variable nonlinearity. Proc. Steklov Inst. Math. 270, 27–42 (2010). https://doi.org/10.1134/S008154381003003X
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S008154381003003X