Abstract
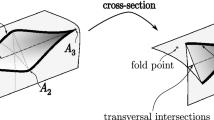
With any stable map from a 3-manifold to ℝ3, we associate a graph with weights in its vertices and edges. These graphs are A-invariants from a global viewpoint. We study their properties and show that any tree with zero weights in its vertices and aleatory weights in its edges can be the graph of a stable map from S 3 to ℝ3.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
V. I. Arnold, “Smooth Functions Statistics,” Funct. Anal. Other Math. 1(2), 125–133 (2006).
V. I. Arnol’d, “Statistics and Classification of Topologies of Periodic Functions and Trigonometric Polynomials,” Tr. Inst. Mat. Mekh., Ural. Otd. Ross. Akad. Nauk 12(1) (2006) [Proc. Steklov Inst. Math., Suppl. 1, S13–S23 (2006)].
V. I. Arnold, “Topological Classification of Morse Functions and Generalisations of Hilbert’s 16th Problem,” Math. Phys. Anal. Geom. 10, 227–236 (2007).
K. A. de Rezende and R. D. Franzosa, “Lyapunov Graphs and Flows on Surfaces,” Trans. Am. Math. Soc. 340(2), 767–784 (1993).
J. Franks, “Nonsingular Smale Flows on S 3,” Topology 24, 265–282 (1985).
M. Golubitsky and V. Guillemin, Stable Mappings and Their Singularities (Springer, New York, 1973), Grad. Texts Math. 14.
D. Hacon, C. Mendes de Jesus, and M. C. Romero Fuster, “Fold Maps from the Sphere to the Plane,” Exp. Math. 15(4), 491–497 (2006).
D. Hacon, C. Mendes de Jesus, and M. C. Romero Fuster, “Stable Maps from Surfaces to the Plane with Prescribed Branching Data,” Topol. Appl. 154(1), 166–175 (2007).
D. Hacon, C. Mendes de Jesus, and M. C. Romero Fuster, “Topological Invariants of Stable Maps from a Surface to the Plane from a Global Viewpoint,” in Real and Complex Singularities (M. Dekker, New York, 2003), Lect. Notes Pure Appl. Math. 232, pp. 227–235.
L. I. Nicolaescu, “Morse Functions Statistics,” Funct. Anal. Other Math. 1(1), 97–103 (2006).
I. Nikolaev, “Graphs and Flows on Surfaces,” Ergodic Theory Dyn. Syst. 18(1), 207–220 (1998).
R. Oset Sinha and M. C. Romero Fuster, “First Order Semi-local Invariants for Stable Maps from 3-Manifolds to ℝ3,” Preprint (Univ. València, 2007).
M. M. Peixoto, “On the Classification of Flows on 2-Manifolds,” in Dynamical Systems: Proc. Sympos. Univ. Bahia, Salvador, 1971 (Acad. Press, New York, 1973), pp. 389–419.
V. Vassiliev, Complements of Discriminants of Smooth Maps: Topology and Applications (Am. Math. Soc., Providence, RI, 1992).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mendes de Jesus, C., Oset Sinha, R. & Romero Fuster, M.C. Global topological invariants of stable maps from 3-manifolds to ℝ3 . Proc. Steklov Inst. Math. 267, 205–216 (2009). https://doi.org/10.1134/S0081543809040178
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0081543809040178