Skip to main content
SpringerLink
Log in

Optimization of the motion in a resistant medium of a body with a movable internal mass

  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

Abstract

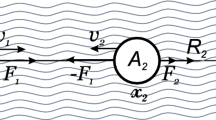
The motion, in a resistant medium, of a system consisting of a rigid body and movable internal mass is considered. The external medium acts on the body by a force that piecewise linearly depends on its speed. The class of periodic motions of the internal mass for which the speed of this mass relative to the body is piecewise constant is studied. It is shown that, under certain conditions, the forward movement of the whole system in the medium is possible. The average speed of this movement over a period is determined. Optimal parameters of the motion of the internal mass for which the average speed of the system movement is maximal are found.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. F. L. Chernousko, Dokl. Akad. Nauk 405(1), 56 (2005).

    Google Scholar 

  2. F. L. Chernousko, in Proceedings of Intern. Seminar on Control Theory and Theory of Generalized Solutions of Hamilton-Jacobi Equations, Ekaterinburg, June 22–26, 2005 (Ekaterinburg, Izd. UrO RNA, 2006), Vol. 1, pp. 55–66.

    Google Scholar 

  3. H. Li, K. Furuta, and F. L. Chernousko, in: Proceedings of Intern. Conf. on Physics and Control, St. Petersburg, Russia, 2003, pp. 15–17.

Download references

Author information

Authors and Affiliations

  1. Institute for Problems in Mechanics, the Russian Academy of Sciences, pr. Vernadskogo 101-1, Moscow, 119526, Russia

    F. L. Chernousko

Authors
  1. F. L. Chernousko
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Original Russian Text © F.L. Chernousko, 2006, published in Trudy Instituta Matematiki i Mekhaniki UrO RAN, 2006, Vol. 12, No. 1.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chernousko, F.L. Optimization of the motion in a resistant medium of a body with a movable internal mass. Proc. Steklov Inst. Math. 253 (Suppl 1), S76–S82 (2006). https://doi.org/10.1134/S0081543806050063

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543806050063

Keywords

Search

Navigation