Skip to main content
SpringerLink
Log in

Mathematical Modeling of Swirled Nonisothermic Flow of Two-Phase Media over Permeable Surfaces

  • American-Russian Chemical Engineering Scientific School “Modeling and Optimization of Chemical Engineering Processes and Systems” May 23–25, 2016 (Kazan National Research Technological University)
  • Published:
Theoretical Foundations of Chemical Engineering Aims and scope Submit manuscript

Abstract

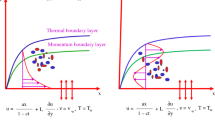
A mathematical model has been developed for the swirled nonisothermal flow of two-phase medium with a free surface along the inner wall of a permeable surface of revolution. Two types of flows have been considered, i.e., flows on rotating nozzles and on fixed circular surfaces of rotation when the medium is fed tangentially. Equations of the conservation of mechanics of heterogeneous media have been solved by the method of surfaces of equal consumption. The results of numerical calculations of flows for a conic surface have been presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Intensifikatsiya teplo-i massoobmena v energetike (Intensification of Heat and Mass Transfer in Power Engineering), Kuzma-Kichta, Yu.A., Ed., Moscow: TsNIIATOMINFORM, 2003.

  2. Shul'man, Z.P. and Baikov, V.I., Reodinamika i teplomassoobmen v plenochnykh techeniyakh (Rheodynamics and Heat and Mass Transfer in Film Flows), Minsk: Nauka i Tekhnika, 1979.

    Google Scholar 

  3. Kholpanov, L.P. and Shkadov, V.Ya., Gidrodinamika i teplomassoobmen s poverkhnost’yu razdela (Interfacial Hydrodynamics and Heat and Mass Transfer), Moscow: Nauka, 1990.

    Google Scholar 

  4. Ibyatov, R.I., Kholpanov, L.P., and Murtazin, T.S., Mathematical simulation of a twisted flow in a cylindrical-conical hydrocyclone, Heat Transfer Res., 2010, vol. 41, no. 1, pp. 41–57. doi 10.1615/HeatTransRes. v41.i1.40

    Article  Google Scholar 

  5. Ibyatov, R.I. and Murtazin, T.Sh., Calculation of the motion of a non-Newtonian dispersion medium in a cylinder-conic hydrocyclone, Vestn. Kazan. Gos. Agrar. Univ., 2010, no. 2 (16), p.102.

    Google Scholar 

  6. Ibyatov, R.I. and Sirazeva, D.F., Calculation of swirling nonisothermal flow of the layer of a two-phase non-Newtonian medium over a conic surface, Vestn. Kazan. Gos. Agrar. Univ., 2016, no. 2 (40), p.68.

    Article  Google Scholar 

  7. Babak, V.N., Babak, T.B., and Kholpanov, L.P., Simultaneous heat and momentum transfer in twophase film systems at low pressure, Theor. Found. Chem. Eng., 2003, vol. 37, no. 4, pp. 313–324. doi 10.1023/A:1025021532405

    Article  CAS  Google Scholar 

  8. Numerical Methods in Fluid Dynamics, Wirz, H.J. and Smolderen, J.J., Eds., Von Karman Institute for Fluid Dynamics Lecture Series, vol. 87, Washington, DC: Hemisphere, 1978.

  9. Roache, P.J., Computational Fluid Dynamics, Albuquerque, N.M.: Hermosa, 1976.

    Google Scholar 

  10. Ibyatov, R.I., Kholpanov, L.P., Akhmadiev, F.G., and Fazylzyanov, R.R., Mathematical modeling of flows of heterogeneous media over rotating permeable surfaces, Theor. Found. Chem. Eng., 2003, vol. 37, no. 5, pp. 447–459. doi 10.1023/A:1026086424153

    Article  CAS  Google Scholar 

  11. Kholpanov, L.P. and Ibyatov, R.I., Simulation of the hydrodynamics of multiphase heterogeneous media in a centrifugal field, Theor. Found. Chem. Eng., 2009, vol. 43, no. 5, pp. 629–641. doi 10.1134/S0040579509050054

    Article  CAS  Google Scholar 

  12. Eroshenko, V.M. and Zaichik, L.I., Gidrodinamika i teplomassoobmen na pronitsaemykh poverkhnostyakh (Hydrodynamics and Heat and Mass Transfer on Permeable Surfaces), Moscow: Nauka, 1984.

    Google Scholar 

  13. Melamed, L.E., Filippov, G.A., and Tropkina, A.I., Fragmentation method of hydrodynamic and thermal analysis of structured systems, Izv. Vyssh. Uchebn. Zaved., Probl. Energ., 2011, no. 3, p.3.

    Google Scholar 

  14. Nigmatulin, R.I., Dinamika mnogofaznykh sred (Dynamics of Multiphase Media), Moscow: Nauka, 1987, part1.

    Google Scholar 

  15. Buevich, Yu.A. and Korneev, Yu.A., Effective thermal conductivity of disperse media at small Peclet number, J. Eng. Phys., 1976, vol. 31, no. 4, pp. 1141–1145. doi 10.1007/BF00861059

    Article  Google Scholar 

  16. Ibyatov, R.I., Kholpanov, L.P., Akhmadiev, F.G., and Fazylzyanov, R.R., Mathematical modeling of phase separation of a multiphase medium, Theor. Found. Chem. Eng., 2006, vol. 40, no. 4, pp. 339–348. doi 10.1134/S0040579506040026

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kazan State Agrarian University, Kazan, 420015 Tatarstan, Russia

    R. I. Ibyatov

Authors
  1. R. I. Ibyatov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. I. Ibyatov.

Additional information

Original Russian Text © R.I. Ibyatov, 2017, published in Teoreticheskie Osnovy Khimicheskoi Tekhnologii, 2017, Vol. 51, No. 6, pp. 649–658.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ibyatov, R.I. Mathematical Modeling of Swirled Nonisothermic Flow of Two-Phase Media over Permeable Surfaces. Theor Found Chem Eng 51, 992–1001 (2017). https://doi.org/10.1134/S0040579517060070

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040579517060070

Keywords

Search

Navigation