Skip to main content
SpringerLink
Log in

Inverse Scattering Transform and Soliton Classification of Higher-Order Nonlinear Schrödinger-Maxwell-Bloch Equations

  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

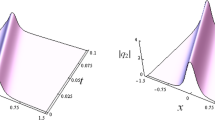
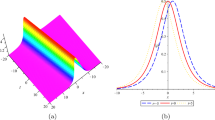
We investigate higher-order nonlinear Schrödinger-Maxwell-Bloch equations using the Riemann-Hilbert method. We perform a spectral analysis of the Lax pair and construct a Riemann-Hilbert problem according to the spectral analysis. As a result, we obtain three types of multisoliton solutions. Based on the analytic solution and with a choice of corresponding parameter values, we obtain solutions of the breather type and a bell-shaped solution and find an interesting phenomenon of the collision of two soliton solutions. We hope that these results can be useful in modeling the wave propagation of a nonlinear optical field in an erbium-doped fiber medium.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. P. Agrawal, Nonlinear Fiber Optics, Acad. Press, New York (2001).

    MATH  Google Scholar 

  2. A. Hasegawa and Y. Kodama, Solitons in Optical Communications, Oxford Univ. Press, Oxford (1995).

    MATH  Google Scholar 

  3. V. E. Zakharov and A. B. Shabat, “Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media,” Sov. Phys. JETP, 34, 62–69 (1972).

    ADS  MathSciNet  Google Scholar 

  4. A. Hasegawa and F. D. Tappert, “Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers: I. Anomalous dispersion,” Appl. Math. Lett., 23, 142–144 (1973).

    ADS  Google Scholar 

  5. K. Porsezian and K. Nakkeeran, “Optical solitons in presence of Kerr dispersion and self-frequency shift,” Phys. Rev. Lett., 76, 3955–3958 (1996); Erratum, 78, 3227 (1997).

    ADS  Google Scholar 

  6. Y. S. Kivshar and G. P. Agrawal, Optical Solitons: From Fibers to Photonic Crystals, Elsevier, New York (2003).

    Google Scholar 

  7. S.-F. Tian and T.-T. Zhang, “Long-time asymptotic behavior for the Gerdjikov-Ivanov type of derivative nonlinear Schrödinger equation with time-periodic boundary condition,” Proc. AMS, 146, 1713–1729 (2018).

    MATH  Google Scholar 

  8. S.-F. Tian, “Initial-boundary value problems for the general coupled nonlinear Schrödinger equation on the interval via the Fokas method,” J. Differ. Equ., 262, 506–558 (2017).

    ADS  MATH  Google Scholar 

  9. S.-F. Tian, “The mixed coupled nonlinear Schrödinger equation on the half-line via the Fokas method,” Proc. Roy. Soc. London Ser. A, 472, 20160588 (2016).

    ADS  MATH  Google Scholar 

  10. W.-Q. Peng, S.-F. Tian, and T.-T. Zhang, “Dynamics of breather waves and higher-order rogue waves in a coupled nonlinear Schrödinger equation,” Europhys. Lett., 123, 50005 (2018).

    ADS  Google Scholar 

  11. D. Guo, S.-F. Tian, T.-T. Zhang, and J. Li, “Modulation instability analysis and soliton solutions of an integrable coupled nonlinear Schrödinger system,” Nonlinear Dyn., 94, 2749–2761 (2018).

    Google Scholar 

  12. K. Nakkeeran, K. Porsezian, P. S. Sundaram, and A. Mahalingam, “Optical solitons in N-coupled higher order nonlinear Schrödinger equations,” Phys. Rev. Lett., 80, 1425–1428 (1998).

    ADS  Google Scholar 

  13. D.-S. Wang, S. Yin, Y. Tian, and Y. Liu, “Integrability and bright soliton solutions to the coupled nonlinear Schrödinger equation with higher-order effects,” Appl. Math. Comput., 229, 296–309 (2014).

    MathSciNet  MATH  Google Scholar 

  14. L.-L. Feng and T.-T. Zhang, “Breather wave, rogue wave, and solitary wave solutions of a coupled nonlinear Schrödinger equation,” Appl. Math. Lett., 78, 133–140 (2018).

    MathSciNet  MATH  Google Scholar 

  15. R. Hirota and J. Satsuma, “Soliton solutions of a coupled Korteweg-de Vries equation,” Phys. Lett. A, 85, 407–408 (1981).

    ADS  MathSciNet  Google Scholar 

  16. S.-F. Tian, “Initial-boundary value problems for the coupled modified Korteweg-de Vries equation on the interval,” Commun. Pure Appl. Anal., 17, 923–957 (2018).

    MathSciNet  MATH  Google Scholar 

  17. S.-F. Tian, “Initial-boundary value problems of the coupled modified Korteweg-de Vries equation on the half-line via the Fokas method,” J. Phys. A: Math. Theor., 50, 395204 (2017).

    MathSciNet  MATH  Google Scholar 

  18. J. Wu and X. Geng, “Inverse scattering transform and soliton classification of the coupled modified Kortewegde Vries equation,” Commun. Nonlinear Sci. Numer. Simul., 53, 83–93 (2017).

    ADS  MathSciNet  Google Scholar 

  19. J. K. Yang and D. J. Kaup, “Squared eigenfunctions for the Sasa-Satsuma equation,” J. Math. Phys., 50, 023504 (2009); arXiv:0902.1210v1 [nlin.SI] (2009).

    ADS  MathSciNet  MATH  Google Scholar 

  20. J. Xu and E. Fan, “The unified transform method for the Sasa-Satsuma equation on the half-line,” Proc. Roy. Soc. London Ser. A, 469, 20130068 (2013).

    ADS  MathSciNet  MATH  Google Scholar 

  21. X. Geng and J. Wu, “Riemann-Hilbert approach and N-soliton solutions for a generalized Sasa-Satsuma equation,” Wave Motion, 60, 62–72 (2016).

    MathSciNet  MATH  Google Scholar 

  22. D. J. Kedziora, A. Ankiewicz, and N. Akhmediev, “Second-order nonlinear Schrödinger equation breather solutions in the degenerate and rogue wave limits,” Phys. Rev. E, 85, 066601 (2012).

    ADS  Google Scholar 

  23. K. Nakkeeran and K. Porsezian, “Solitons in an erbium-doped nonlinear fibre medium with stimulated inelastic scattering,” J. Phys. A: Mat. Gen., 28, 3817–3823 (1995).

    ADS  MathSciNet  MATH  Google Scholar 

  24. K. Nakkeeran and K. Porsezian, “Coexistence of a self-induced transparency soliton and a higher order nonlinear Schrödinger soliton in an erbium doped fiber,” Opt. Commun., 123, 169–174 (1996).

    ADS  Google Scholar 

  25. K. Nakkeeran, “Optical solitons in erbium doped fibers with higher order effects,” Phys. Lett. A, 275, 415–418 (2000).

    ADS  MATH  Google Scholar 

  26. K. Nakkeeran, “Optical solitons in erbium-doped fibres with higher-order effects and pumping,” J. Phys. A., 33, 4377–4382 (2000).

    ADS  MathSciNet  MATH  Google Scholar 

  27. R. Guo and H.-Q. Hao, “Breathers and localized solitons for the Hirota-Maxwell-Bloch system on constant backgrounds in erbium doped fibers,” Ann. Phys., 344, 10–16 (2014).

    ADS  MATH  Google Scholar 

  28. K. Porsezian, A. Mahalingam, and P. Shanmugha Sundaram, “Integrability aspects of NLS-MB system with variable dispersion and nonlinear effects,” Chaos, Solitons and Fractals, 12, 1137–1143 (2001).

    ADS  MATH  Google Scholar 

  29. Y.-S. Xue, B. Tian, W.-B. Ai, M. Li, and P. Wang, “Integrability and optical solitons in a generalized variable-coefficient coupled Hirota-Maxwell-Bloch system in fiber optics,” Opt. Laser Technol., 48, 153–159 (2013).

    ADS  Google Scholar 

  30. M. J. Ablowitz and A. S. Fokas, Complex Variables: Introduction and Applications, Cambridge Univ. Press, Cambridge (2003).

    MATH  Google Scholar 

  31. M. J. Ablowitz and P. A. Clarkson, Solitons, Nonlinear Evolution Equations, and Inverse Scattering (London Math. Soc. Lect. Note Ser., Vol. 149), Cambridge Univ. Press, Cambridge (1991).

    MATH  Google Scholar 

  32. L. A. Takhtajan and L. D. Faddeev, Hamiltonian Approach to the Theory of Solitons [in Russian], Nauka, Moscow (1986)

    Google Scholar 

  33. English transl.: L. D. Faddeev and L. A. Takhtajan, Hamiltonian Methods in the Theory of Solitons, Springer, Berlin (1987).

    MATH  Google Scholar 

  34. J. Yang, Nonlinear Waves in Integrable and Nonintegrable Systems (Math. Model. Comput., Vol. 16), SIAM, Philadelphia (2010).

    MATH  Google Scholar 

  35. V. S. Shchesnovich and J. Yang, “General soliton matrices in the Riemann-Hilbert problem for integrable nonlinear equations,” J. Math. Phys., 44, 4604–4639 (2003); arXiv:nlin/0306027v1 (2003).

    ADS  MathSciNet  MATH  Google Scholar 

  36. D.-S. Wang, D.-J. Zhang, and J. Yang, “Integrable properties of the general coupled nonlinear Schrödinger equations,” J. Math. Phys., 51, 023510 (2010).

    ADS  MathSciNet  MATH  Google Scholar 

  37. B. Guo and L. Ling, “Riemann-Hilbert approach and N-soliton formula for coupled derivative Schrödinger equation,” J. Math. Phys., 53, 073506 (2012).

    ADS  MathSciNet  MATH  Google Scholar 

  38. J. J. Yang, S. F. Tian, W. Q. Peng, and T. T. Zhang, “The N-coupled higher-order nonlinear Schrödinger equation: Riemann-Hilbert problem and multi-soliton solutions,” Math. Meth. Appl. Sci., 43, 2458–2472 (2020).

    Google Scholar 

  39. J. Xu and E. Fan, “Long-time asymptotics for the Fokas-Lenells equation with decaying initial value problem: Without solitons,” J. Differ. Equ., 259, 1098–1148 (2015).

    ADS  MathSciNet  MATH  Google Scholar 

  40. Z. Yan, “An initial-boundary value problem for the integrable spin-1 Gross-Pitaevskii equations with a 4×4 Lax pair on the half-line,” Chaos, 27, 053117 (2017); arXiv:1704.08534v1 [nlin.SI] (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  41. J.-P. Wu and X.-G. Geng, “Inverse scattering transform of the coupled Sasa-Satsuma equation by Riemann-Hilbert approach,” Commun. Theor. Phys., 67, 527–534 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  42. W.-X. Ma, “Riemann-Hilbert problems and N-soliton solutions for a coupled mKdV system,” J. Geom. Phys., 132, 45–54 (2018).

    ADS  MathSciNet  MATH  Google Scholar 

  43. A. V. Mikhailov and V. Yu. Novokshenov, “The Riemann-Hilbert problem for analytic description of the DM solitons,” Theor. Math. Phys., 137, 1723–1732 (2003).

    MATH  Google Scholar 

  44. A. R. Its and N. A. Slavnov, “On the Riemann-Hilbert approach to asymptotic analysis of the correlation functions of the quantum nonlinear Schrödinger equation: Interacting fermion case,” Theor. Math. Phys., 119, 541–593 (1999).

    MATH  Google Scholar 

  45. Y. Zhang, Y. Cheng, and J. He, “Riemann-Hilbert method and N-soliton for two-component Gerdjikov-Ivanov equation,” J. Nonliner Math. Phys., 24, 210–223 (2017).

    MathSciNet  MATH  Google Scholar 

  46. A. P. Fordy and P. P. Kulish, “Nonlinear Schrödinger equations and simple Lie algebras,” Commun. Math. Phys., 89, 427–443 (1983).

    ADS  MATH  Google Scholar 

  47. V. S. Gerdjikov, “Basic aspects of soliton theory,” in: Geometry, Integrability, and Quantization (Sts. Constantine and Elena, Bulgaria, 3–10 June 2004, I. M. Mladenov and A. C. Hirshfeld, eds.), Bulgarian Acad. Sci., Sofia (2005), pp. 78–25.

    Google Scholar 

  48. V. E. Zakharov, S. V. Manakov, S. P. Novikov, and L. I. Pitaevskii, Theory of Solitons: The Inverse Scattering Method [in Russian], Nauka, Moscow (1980); English transl., Plenum Press (Consultants Bureau), New York (1984).

    MATH  Google Scholar 

  49. V. E. Zakharov and A. B. Shabat, “Integration of nonlinear equations of mathematical physics by the method of inverse scattering: II,” Funct. Anal. Appl., 13, No. 3, 166–174 (1979).

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors thank the editor and the referees for their valuable comments and suggestions.

Author information

Authors and Affiliations

  1. School of Mathematics and Institute of Mathematical Physics, China University of Mining and Technology, Xuzhou, China

    Zhi-Qiang Li, Shou-Fu Tian, Wei-Qi Peng & Jin-Jie Yang

Authors
  1. Zhi-Qiang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shou-Fu Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei-Qi Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jin-Jie Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shou-Fu Tian.

Additional information

Conflicts of interest

The authors declare no conflicts of interest.

This research was supported by the Postgraduate Research and Practice of Educational Reform for Graduate students in CUMT (Grant No. 2019YJSJG046), the Natural Science Foundation of Jiangsu Province (Grant No. BK20181351), the Six Talent Peaks Project in Jiangsu Province (Grant No. JY-059), the Qinglan Project of Jiangsu Province of China, the National Natural Science Foundation of China (Grant No. 11975306), the Fundamental Research Fund for the Central Universities (Grant Nos. 2019ZDPY07 and 2019QNA35), and the General Financial Grant from the China Postdoctoral Science Foundation (Grant Nos. 2015M570498 and 2017T100413).

Prepared from an English manuscript submitted by the authors; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, Vol. 203, No. 3, pp. 323–341, June, 2020.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, ZQ., Tian, SF., Peng, WQ. et al. Inverse Scattering Transform and Soliton Classification of Higher-Order Nonlinear Schrödinger-Maxwell-Bloch Equations. Theor Math Phys 203, 709–725 (2020). https://doi.org/10.1134/S004057792006001X

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S004057792006001X

Keywords

Search

Navigation