Abstract
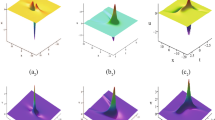
Nonlinear generalizations of integrable equations in one dimension, such as the Korteweg–de Vries and Boussinesq equations with p-power nonlinearities, arise in many physical applications and are interesting from the analytic standpoint because of their critical behavior. We study analogous nonlinear p-power generalizations of the integrable Kadomtsev–Petviashvili and Boussinesq equations in two dimensions. For all p ≠ 0, we present a Hamiltonian formulation of these two generalized equations. We derive all Lie symmetries including those that exist for special powers p ≠ 0. We use Noether’s theorem to obtain conservation laws arising from the variational Lie symmetries. Finally, we obtain explicit line soliton solutions for all powers p > 0 and discuss some of their properties.
Similar content being viewed by others
References
M. J. Ablowitz and H. Segur, “On the evolution of packets of water waves,” J. Fluid Mech., 92, 691–715 (1979).
B. B. Kadomstev and V. I. Petviashvili, “On the stability of waves in weakly dispersive media,” Sov. Phys. Dokl., 15, 539–541 (1970).
V. Veerakumar and M. Daniel, “Modified Kadomtsev–Petviashvili (MKP) equation and electromagnetic soliton,” Math. Comput. Simulation, 62, 163–169 (2003).
J. Satsuma, “N-soliton solution of the two-dimensional Korteweg–deVries equation,” J. Phys. Soc. Japan, 40, 286–290 (1976).
J. Satsuma and M. J. Ablowitz, “Two-dimensional lumps in nonlinear dispersive systems,” J. Math. Phys., 20, 1496–1503 (1979).
S. V. Manakov, V. E. Zakharov, L. A. Bordag, A. R. Its, and V. B. Matveev, “Two-dimensional solitons of the Kadomtsev–Petviashvili equation and their interaction,” Phys. Lett. A, 63, 205–206 (1977).
F. Gesztesy, H. Holden, E. Saab, and B. Simon, “Explicit construction of solutions of the modified Kadomtsev–Petviashvili equation,” J. Funct. Anal., 98, 211–228 (1991).
B. G. Konopel’chenko and V. G. Dubrovsky, “Inverse spectral transform for the modified Kadomtsev–Petviashvili equation,” Stud. Appl. Math., 86, 219–268 (1992).
T. Tao, “Why are solitons stable?” Bull. Amer. Math. Soc., n.s., 46, 1–33 (2009).
L. V. Bogdanov and V. E. Zakharov, “The Boussinesq equation revisited,” Phys. D, 165, 137–162 (2002).
G. E. Falkovich, M. D. Spector, and S. K. Turitsyn, “Destruction of stationary solutions and collapse in the nonlinear string equation,” Phys. Lett. A, 99, 271–274 (1983).
R. Naz, Z. Ali, and I. Naeem, “Reductions and new exact solutions of ZK, Gardner KP, and modified KP equations via generalized double reduction theorem,” Abstr. Appl. Anal., 2013, 340564 (2013).
W. Rui, P. Zhao, and Y. Zhang, “Invariant solutions and conservation laws of the (2+1)-dimensional Boussinesq equation,” Abstr. Appl. Anal., 2014, 840405 (2014).
A. R. Adem, C. M. Khalique, and A. Biswas, “Solutions of Kadomtsev–Petviashvili equation with power law nonlinearity in 1+3 dimensions,” Math. Meth. Appl. Sci., 34, 532–543 (2010).
P. J. Olver, Applications of Lie Groups to Differential Equations, Springer, New York (1993).
G. W. Bluman, A. F. Cheviakov, and S. C. Anco, Applications of Symmetry Methods to Partial Differential Equations (Appl. Math. Sci., Vol. 168), Springer, New York (2010).
S. C. Anco and G. Bluman, “Direct construction method for conservation laws of partial differential equations: Part II. General treatment,” Eur. J. Appl. Math., 13, 567–585 (2002).
L. A. Dickey, “On Hamiltonian and Lagrangian formalisms for the KP-hierarchy of integrable equations,” Ann. Acad. Sci. (N. Y.), 491, 131–148 (1987).
S. C. Anco, E. Recio, M. Gandarias, and M. Bruzón, “A nonlinear generalization of the Camassa–Holm equation with peakon solutions,” in: Dynamical Systems, Differential Equations, and Applications (Proc. 10th AIMS Conf., M. de Leon, W. Feng, Z. Feng, J. Lopez-Gomez, X. Lu, J. M. Martell, J. Parcet, D. Peralta-Salas, and W. Ruan, eds.), AIMS, Madrid, Spain (2015), pp. 29–37.
S. Y. Lou, “Symmetries of the Kadomtsev–Petviashvili equation,” J. Phys. A: Math. Gen., 26, 4387–4394 (1993).
S. C. Anco, “Generalization of Noether’s theorem in modern form to non-variational partial differential equations,” in: Recent Progress and Modern Challenges in Applied Mathematics, Modeling, and Computational Science (Fields Inst. Commun., Vol. 79), Springer, New York (2017), pp. 119–182.
T. Wolf, “A comparison of four approaches to the calculation of conservation laws,” Eur. J. Appl. Math., 13, 129–152 (2002).
S. C. Anco and A. Kara, “Symmetry-invariant conservation laws of partial differential equations,” Eur. J. Appl. Math., 29, 78–117 (2017).
I. S. O’Keir and E. J. Parkes, “The derivation of a modified Kadomtsev–Petviashvili equation and the stability of its solutions,” Phys. Scr., 55, 135–142 (1997).
M. Matsukawa, S. Watanaba, and H. Tanaca, “Soliton solutions of generalized 2D Boussinesq equation with quadratic and cubic nonlinearity,” J. Phys. Soc. Japan, 58, 827–830 (1989).
Author information
Authors and Affiliations
Corresponding author
Additional information
Prepared from an English manuscript submitted by the authors; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, Vol. 197, No. 1, pp. 3–23, October, 2018.
Rights and permissions
About this article
Cite this article
Anco, S.C., Gandarias, M.L. & Recio, E. Conservation Laws, Symmetries, and Line Soliton Solutions of Generalized KP and Boussinesq Equations with p-Power Nonlinearities in Two Dimensions. Theor Math Phys 197, 1393–1411 (2018). https://doi.org/10.1134/S004057791810001X
Published:
Issue Date:
DOI: https://doi.org/10.1134/S004057791810001X