Skip to main content
SpringerLink
Log in

The method of uniqueness and the optical conductivity of graphene: New application of a powerful technique for multiloop calculations

  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

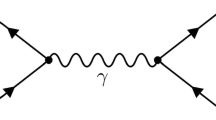
We briefly review the uniqueness method, which is a powerful technique for calculating multiloop Feynman diagrams in theories with conformal symmetries. We use the method in the momentum space and show its effectiveness in calculating a two-loop massless propagator Feynman diagram with a noninteger index on the central line. We use the obtained result to compute the optical conductivity of graphene at the infrared Lorentz-invariant fixed point. We analyze the effect of counterterms and compare with the nonrelativistic limit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. N. Vasil’ev, Yu. M. Pis’mak, and Yu. R. Khonkonen, “1/n Expansion: Calculation of the exponents η and v in the order 1/n2 for arbitrary number,” Theor. Math. Phys., 47, 465–475 (1981).

    Article  Google Scholar 

  2. K. G. Chetyrkin and F. V. Tkachov, “Integration by parts: The algorithm to calculate ß-functions in 4 loops,” Nucl. Phys. B, 192, 159–204 (1981)

    Article  ADS  Google Scholar 

  3. F. V. Tkachov, “A theorem on analytical calculability of 4-loop renormalization group functions,” Phys. Lett. B, 100, 65–68 (1981).

    Article  ADS  MathSciNet  Google Scholar 

  4. S. Laporta, “High-precision calculation of multiloop Feynman integrals by difference equations,” Internat. J. Modern Phys. A, 15, 5087–5159 (2000).

    ADS  MathSciNet  MATH  Google Scholar 

  5. K. G. Chetyrkin, A. L. Kataev, and F. V. Tkachov, “New approach to evaluation of multiloop Feynman integrals: The Gegenbauer polynomial x-space technique,” Nucl. Phys. B, 174, 345–377 (1980).

    Article  ADS  MathSciNet  Google Scholar 

  6. A. V. Kotikov, “The Gegenbauer polynomial technique: The evaluation of a class of Feynman diagrams,” Phys. Lett. B, 375, 240–248 (1996).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. M. D’Eramo, L. Pelitti, and G. Parisi, “Theoretical predictions for critical exponents at the η-point of Bose liquids,” Lett. Nuovo Cimento, 2, 878–880 (1971).

    Article  Google Scholar 

  8. N. I. Usyukina, “Calculation of many-loop diagrams of perturbation theory,” Theor. Math. Phys., 54, 78–81 (1983).

    Article  Google Scholar 

  9. D. I. Kazakov, “Calculation of Feynman diagrams by the ‘Uniqueness’ method,” Theor. Math. Phys., 58, 223–230 (1984).

    Article  Google Scholar 

  10. D. I. Kazakov, “Many-loop calculations: The uniqueness method and functional equations,” Theor. Math. Phys., 62, 84–89 (1985)

    Article  Google Scholar 

  11. D. I. Kazakov, “The method of uniqueness, a new powerful technique for multiloop calculations,” Phys. Lett. B, 133, 406–410 (1983).

    Article  ADS  Google Scholar 

  12. D. I. Kazakov, “Analytical methods for multiloop calculations: Two lectures on the method of uniqueness,” Preprint JINR E2-84-410, Joint Inst. Nucl. Res., Dubna (1984).

    Google Scholar 

  13. A. G. Grozin, “Massless two-loop self-energy diagram: Historical review,” Internat. J. Modern Phys. A, 27, 1230018 (2012).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. D. J. Broadhurst, “Exploiting the 1, 440-fold symmetry of the master two-loop diagram,” Z. Phys. C: Part. Fields, 32, 249–253 (1986).

    Article  Google Scholar 

  15. D. T. Barfoot and D. J. Broadhurst, “Z2×S6 symmetry of the two-loop diagram,” Z. Phys. C, 41, 81–85 (1988).

    Article  MathSciNet  Google Scholar 

  16. J. A. Gracey, “On the evaluation of massless Feynman diagrams by the method of uniqueness,” Phys. Lett. B, 277, 469–473 (1992).

    Article  ADS  MathSciNet  Google Scholar 

  17. N. A. Kivel, A. S. Stepanenko, and A. N. Vasil’ev, “On the calculation of 2+e RG functions in the Gross–Neveu model from large-N expansions of critical exponents,” Nucl. Phys. B, 424, 619–627 (1994)

    Article  ADS  Google Scholar 

  18. A. N. Vasil’ev, S. E. Derkachev, N. A. Kivel’, and A. S. Stepanenko, “The 1/n expansion in the Gross–Neveu model: Conformal bootstrap calculation of the index η in order 1/n3,” Theor. Math. Phys., 94, 127–136 (1993); arXiv:hep-th/ 9302034v2 (1993).

    Article  Google Scholar 

  19. D. J. Broadhurst, J. A. Gracey, and D. Kreimer, “Beyond the triangle and uniqueness relations: Non-zeta counterterms at large N from positive knots,” Z. Phys. C, 75, 559–574 (1997).

    Article  MathSciNet  Google Scholar 

  20. D. J. Broadhurst and A. V. Kotikov, “Compact analytical form for non-zeta terms in critical exponents at order 1/N3,” Phys. Lett. B, 441, 345–353 (1998).

    Article  ADS  Google Scholar 

  21. D. J. Broadhurst, “Where do the tedious products of’ s come from?” Nucl. Phys. Proc. Suppl., 116, 432–436 (2003).

    Article  ADS  MATH  Google Scholar 

  22. I. Bierenbaum and S. Weinzierl, “The massless two-loop two-point function,” Eur. Phys. J. C, 32, 67–78 (2003).

    Article  ADS  MATH  Google Scholar 

  23. A. V. Kotikov and S. Teber, “Note on an application of the method of uniqueness to reduced quantum electrodynamics,” Phys. Rev. D, 87, 087701 (2013).

    Article  ADS  Google Scholar 

  24. A. V. Kotikov and S. Teber, “Two-loop fermion self-energy in reduced quantum electrodynamics and application to the ultrarelativistic limit of graphene,” Phys. Rev. D, 89, 065038 (2014).

    Article  ADS  Google Scholar 

  25. S. Teber, “Electromagnetic current correlations in reduced quantum electrodynamics,” Phys. Rev. D, 86, 025005 (2012).

    Article  ADS  Google Scholar 

  26. J. González, F. Guinea, and M. A. H. Vozmediano, “Non-Fermi liquid behavior of electrons in the half-filled honeycomb lattice (A renormalization group approach),” Nucl. Phys. B, 424, 595–618 (1994).

    Article  ADS  Google Scholar 

  27. D. C. Elias, R. V. Gorbachev, A. S. Mayorov, S. V. Morozov, A. A. Zhukov, P. Blake, L. A. Ponomarenko, I. V. Grigorieva, K. S. Novoselov, F. Guinea, and A. K. Geim, “Dirac cones reshaped by interaction effects in suspended graphene,” Nature Phys., 7, 701–704 (2011).

    Article  ADS  Google Scholar 

  28. E. V. Gorbar, V. P. Gusynin, and V. A. Miransky, “Dynamical chiral symmetry breaking on a brane in reduced QED,” Phys. Rev. D, 64, 105028 (2001).

    Article  ADS  Google Scholar 

  29. E. C. Marino, “Quantum electrodynamics of particles on a plane and the Chern–Simons theory,” Nucl. Phys. B, 408, 551–564 (1993)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  30. N. Dorey and N. E. Mavromatos, “QED3 and two-dimensional superconductivity without parity violation,” Nucl. Phys. B, 386, 614–680 (1992)

    Article  ADS  Google Scholar 

  31. A. Kovner and B. Rosenstein, “Kosterlitz–Thouless mechanism of two-dimensional superconductivity,” Phys. Rev. B, 42, 4748–4751 (1990).

    Article  ADS  Google Scholar 

  32. A. W. W. Ludwig, M. P. A. Fisher, R. Shankar, and G. Grinstein, “Integer quantum Hall transition: An alternative approach and exact results,” Phys. Rev. B, 50, 7526–7552 (1994).

    Article  ADS  Google Scholar 

  33. E. G. Mishchenko, “Minimal conductivity in graphene: Interaction corrections and ultraviolet anomaly,” Europhys. Lett., 83, 17005 (2008).

    Article  ADS  Google Scholar 

  34. I. F. Herbut, V. Juričić, and O. Vafek, “Coulomb interaction, ripples, and the minimal conductivity of graphene,” Phys. Rev. Lett., 100, 046403 (2008)

    Article  ADS  Google Scholar 

  35. D. E. Sheehy and J. Schmalian, “Optical transparency of graphene as determined by the fine-structure constant,” Phys. Rev. B, 80, 193411 (2009)

    Article  ADS  Google Scholar 

  36. V. Juričić, O. Vafek, and I. F. Herbut, “Conductivity of interacting massless Dirac particles in graphene: Collisionless regime,” Phys. Rev. B, 82, 235402 (2010)

    Article  ADS  Google Scholar 

  37. F. de Juan, A. G. Grushin, and M. A. H. Vozmediano, “Renormalization of Coulomb interaction in graphene: Determining observable quantities,” Phys. Rev. B, 82, 125409 (2010)

    Article  ADS  Google Scholar 

  38. S. H. Abedinpour, G. Vignale, A. Principi, M. Polini, W-K. Tse, and A. H. MacDonald, “Drude weight, plasmon dispersion, and ac conductivity in doped graphene sheets,” Phys. Rev. B, 84, 045429 (2011)

    Article  ADS  Google Scholar 

  39. I. Sodemann and M. M. Fogler, “Interaction corrections to the polarization function of graphene,” Phys. Rev. B, 86, 115408 (2012)

    Article  ADS  Google Scholar 

  40. B. Rosenstein, M. Lewkowicz, and T. Maniv, “Chiral anomaly and strength of the electron-electron interaction in graphene,” Phys. Rev. Lett., 110, 066602 (2013)

    Article  ADS  Google Scholar 

  41. G. Gazzola, A. L. Cherchiglia, L. A. Cabral, M. C. Nemes, and M. Sampaio, “Conductivity of Coulomb interacting massless Dirac particles in graphene: Regularization-dependent parameters and symmetry constraints,” Europhys. Lett., 104, 27002 (2013);arXiv:1305.6334v3 [cond-mat.mes-hall] (2013)

    Article  ADS  Google Scholar 

  42. J. Link, P. P. Orth, D. E. Sheehy, and J. Schmalian, “Universal collisionless transport of graphene,” Phys. Rev. B, 93, 235447 (2016);arXiv:1511.05984v1 [cond-mat.str-el] (2015).

    Article  ADS  Google Scholar 

  43. S. Teber and A. V. Kotikov, “Interaction corrections to the minimal conductivity of graphene via dimensional regularization,” Europhys. Lett., 107, 57001 (2014).

    Article  ADS  Google Scholar 

  44. A. Giuliani, V. Mastropietro, and M. Porta, “Absence of interaction corrections in the optical conductivity of graphene,” Phys. Rev. B, 83, 195401 (2011).

    Article  ADS  Google Scholar 

  45. I. F. Herbut and V. Mastropietro, “Universal conductivity of graphene in the ultrarelativistic regime,” Phys. Rev. B, 87, 205445 (2013).

    Article  ADS  Google Scholar 

  46. K. F. Mak, M. Y. Sfeir, Y. Wu, C. H. Lui, J. A. Misewich, and T. F. Heinz, “Measurement of the optical conductivity of graphene,” Phys. Rev. Lett., 101, 196405 (2008)

    Article  ADS  Google Scholar 

  47. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres, and A. K. Geim, “Fine structure constant defines visual transparency of graphene,” Science, 320, 1308 (2008).

    Article  ADS  Google Scholar 

  48. N. M. R. Peres, “The transport properties of graphene: An introduction,” Rev. Modern Phys., 82, 2673–2700 (2010).

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Université Pierre et Marie Curie, Sorbonne Universités, Paris, France

    S. Teber

  2. Laboratoire de Physique Théorique et Hautes Energies, CNRS, Université Pierre et Marie Curie (Paris 6), Paris, France

    S. Teber

  3. Bogoliubov Laboratory of Theoretical Physics, Joint Institute for Nuclear Research, Dubna, Moscow Oblast, Russia

    A. V. Kotikov

Authors
  1. S. Teber
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. V. Kotikov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Teber.

Additional information

The research of A. V. Kotikov was supported by the Russian Foundation for Basic Research (Grant No. 16-02-00790_a).

[The original English version of this paper presented at the conference and submitted to the journal is available at https://arxiv.org/abs/1602.01962.]

Translated from Teoreticheskaya i Matematicheskaya Fizika, Vol. 190, No. 3, pp. 519–532, March, 2017.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Teber, S., Kotikov, A.V. The method of uniqueness and the optical conductivity of graphene: New application of a powerful technique for multiloop calculations. Theor Math Phys 190, 446–457 (2017). https://doi.org/10.1134/S004057791703014X

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S004057791703014X

Keywords

Search

Navigation