Abstract
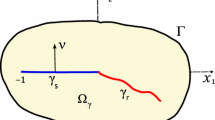
Under study are the boundary value problems that describe the equilibria of two-dimensional elastic bodies with thin weakly curved inclusions in the presence of delamination, which means that there is a crack between the inclusions and an elastic body. Some inequality-type nonlinear boundary conditions are imposed on the crack faces that exclude mutual penetration. This puts the problems into the class of those with unknown contact area. We assume that the inclusions have a contact point, find boundary conditions at the junction point, and justify passage to infinity with respect to the rigidity parameter of the thin inclusion. In particular, we obtain and analyze limit models.
Similar content being viewed by others
References
Khludnev A. M.,Elasticity Problems in Nonsmooth Domains [Russian], Fizmatlit, Moscow (2010).
Khludnev A. M. and Kovtunenko V. A.,Analysis of Cracks in Solids, WIT Press, Southampton and Boston (2000).
Kovtunenko V. A. and Leugering G., “A shape-topological control problem for nonlinear crack-defect interaction: the anti-plane variational model,” SIAM J. Control Optim., vol. 54, no. 3, 1329–1351 (2016).
Knees D. and Mielke A., “Energy release rate for cracks in finite-strain elasticity,” Math. Methods Appl. Sci., vol. 31, no. 5, 501–518 (2008).
Knees D. and Schroder A., “Global spatial regularity for elasticity models with cracks, contact and other nonsmooth constraints,” Math. Methods Appl. Sci., vol. 35, no. 15, 1859–1884 (2012).
Lazarev N. P. and Rudoy E. M., “Shape sensitivity analysis of Timoshenko’s plate with a crack under the nonpenetration condition,” Z. Angew. Math. Mech., vol. 94, no. 9, 730–739 (2014).
Rudoy E. M., “Asymptotics of the energy functional for a fourth-order mixed boundary value problem in a domain with a cut,” Sib. Math. J., vol. 50, no. 2, 341–354 (2009).
Khludnev A. M. and Leugering G. R., “On Timoshenko thin elastic inclusions inside elastic bodies,” Math. Mech. Solids, vol. 20, no. 5, 495–511 (2015).
Rudoy E. M., “Asymptotic behavior of the energy functional for a three-dimensional body with a rigid inclusion and a crack,” J. Appl. Mech. Tech. Phys., vol. 52, no. 2, 252–263 (2011).
Rudoy E. M., “Shape derivative of the energy functional in a problem for a thin rigid inclusion in an elastic body,” Z. Angew. Math. Phys., vol. 66, no. 4, 1923–1937 (2015).
Khludnev A. M., “A weakly curved inclusion in an elastic body with separation,” Mechanics of Solids, vol. 50, no. 5, 591–601 (2015).
Shcherbakov V. V., “On an optimal control problem for the shape of thin inclusions in elastic bodies,” J. Appl. Ind. Math., vol. 7, no. 3, 435–443 (2013).
Shcherbakov V. V., “Choosing an optimal shape of thin rigid inclusions in elastic bodies,” J. Appl. Mech. Tech. Phys., vol. 56, no. 2, 321–329 (2015).
Lazarev N. P., “Shape sensitivity analysis of the energy integrals for the Timoshenko-type plate containing a crack on the boundary of a rigid inclusion,” Z. Angew. Math. Phys., vol. 66, no. 4, 2025–2040 (2015).
Le Dret H., “Modeling of the junction between two rods,” J. Math. Pures Appl., vol. 68, 365–397 (1989).
Le Dret H., “Modeling of a folded plate,” Computational Mechanics, vol. 5, no. 6, 401–416 (1990).
Ciarlet P. G., Le Dret H., and Nzengwa R., “Junctions between three dimensional and two dimensional linearly elastic structures,” J. Math. Pures Appl., vol. 68, no. 3, 261–295 (1989).
Titeux I. and Sanchez-Palencia E., “Junction of thin plates,” Eur. J. Mech. A Solids, vol. 19, no. 3, 377–400 (2000).
Gaudiello A. and Zappale E., “Junction in a thin multidomain for a fourth order problem,” Math. Models Methods Appl. Sci., vol. 16, no. 12, 1887–1918 (2006).
Gaudiello A., Monneau R., Mossino J., Mura F., and Sili A., “Junction of elastic plates and beams,” ESAIM Control Optim. Calc. Var., vol. 13, no. 3, 419–457 (2007).
Neustroeva N. V. and Lazarev N. P., “The junction problem for Euler–Bernoulli and Timoshenko elastic beams,” Sib. Èlektron. Mat. Izv., vol. 13, 26–37 (2016).
Bogan Yu. A., “On the Samarskii–Andreev transmission conditions in the theory of elastic beams,” Math. Notes, vol. 92, no. 5, 606–611 (2012).
Khludnev A. M., Faella L., and Popova T. S., “Junction problem for rigid and Timoshenko elastic inclusions in elastic bodies,” Math. Mech. Solids, vol. 22, no. 4, 737–750 (2017).
Faella L. and Khludnev A. M., “Junction problem for elastic and rigid inclusions in elastic bodies,” Math. Methods Appl. Sci., vol. 39, no. 12, 3381–3390 (2016).
Khludnev A. M. and Popova T. S., “Junction problem for rigid and semi-rigid inclusions in elastic bodies,” Arch. Appl. Mech., vol. 86, no. 9, 1565–1577 (2016).
Khludnev A. M. and Popova T. S., “Junction problem for Euler–Bernoulli and Timoshenko elastic inclusions in elastic bodies,” Quart. Appl. Math., vol. 74, no. 4, 705–718 (2016).
Khludnev A. M. and Popova T. S., “On the mechanical interplay between Timoshenko and semirigid inclusions embedded in elastic bodies,” Z. Angew. Math. Mech., vol. 97, no. 11, 1406–1417 (2017).
Khludnev A. M. and Popova T. S., “Semirigid inclusions in elastic bodies: Mechanical interplay and optimal control,” Comput. Math. Appl., vol. 77, no. 1, 253–262 (2019).
Volmir A. S.,The Nonlinear Dynamics of Plates and Shells [Russian], Nauka, Moscow (1972).
Funding
The work is supported by the Mathematical Center in Akademgorodok under Agreement no. 075–15–2019–1613 with the Ministry of Science and Higher Education of the Russian Federation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Khludnev, A.M., Popova, T.S. The Junction Problem for Two Weakly Curved Inclusions in an Elastic Body. Sib Math J 61, 743–754 (2020). https://doi.org/10.1134/S003744662004014X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S003744662004014X