Tolerance of continuous-variables quantum key distribution to the noise in state preparation

Abstract

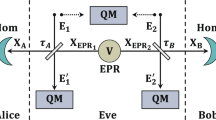
We address the applicability of the continuous-variables quantum key distribution in the realistic conditions of noisy preparation, channel loss and detection noise and investigate the possibility to increase its tolerance to the state preparation noise. The two types of preparation noise, either phase-sensitive or phase-insensitive excess noise, are considered in the assumption of optimal attacks performed by an eavesdropper within the setup based on the entangled source and either homodyne or heterodyne measurements. We show that preparation noise is destructive for the secure channel upon even low noise variances in the conditions of channel loss, while detection noise just decreases the key rate. We propose the method of sender-side attenuation to suppress the preparation noise in the entanglements-based scheme and show that it enables the secure key transmission upon arbitrary high preparation noise of both types and any pure channel loss against both individual and collective attacks.