Skip to main content
SpringerLink
Log in

Flow of a thixotropic fluid over an exponentially stretching sheet with heat transfer

  • Published:
Journal of Applied Mechanics and Technical Physics Aims and scope

Abstract

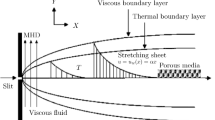
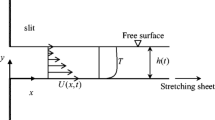
This article addresses the boundary layer flow of a thixotropic fluid past an exponentially stretching sheet with heat transfer. The governing partial differential equations are reduced to an ordinary differential equation whose solution is found by the homotopy analysis method. The numerical values of the skin friction coefficient and Nusselt number are compared with available data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Wang and W. C. Tan, “Stability Analysis of Soret-Driven Double-Diffusive Convection of Maxwell Fluid in a Porous Medium,” Int. J. Heat Fluid Flow 32, 88–94 (2011).

    Article  Google Scholar 

  2. M. Pakdemirli, T. Hayat, M. Yürüsoy, et al., “Perturbation Analysis of a Modified Second Grade Fluid over a Porous Plate,” Nonlinear Anal.: Real World Appl. 12, 1774–1785 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  3. M. Jamil and C. Fetecau, “Some Exact Solutions for Rotating Flows of a Generalized Burgers’ Fluid in Cylindrical Domains,” J. Non-Newtonian Fluid Mech. 165, 1700–1712 (2010).

    Article  MATH  Google Scholar 

  4. T. Hayat, S. A. Shehzad, M. Qasim, and S. Obaidat, “Steady Flow of Maxwell Fluid with Convective Boundary Conditions,” Z. Naturforsch. Ser. A 66a, 417–422 (2011).

    Article  ADS  Google Scholar 

  5. M. M. Rashidi, S. A. M. Pour, and S. Abbasbandy, “Analytic Approximate Solutions for Heat Transfer of a Micropolar Fluid through a Porous Medium with Radiation,” Comm. Nonlinear Sci. Numer. Simulat. 16, 1874–1889 (2011).

    Article  ADS  Google Scholar 

  6. M. A. A. Mahmoud and A. M. Megahed, “Effects of Viscous Dissipation and Heat Generation (Absorption) in a Thermal Boundary Layer of a Non-Newtonian Fluid over a Continuously Moving Permeable Flat Plate,” J. Appl. Mech. Tech. Phys. 50 (5), 819–825 (2009).

    Article  ADS  MATH  Google Scholar 

  7. S. Sadeqi, N. Khabazi, and K. Sadeghy, “Blasius Flow of Thixotropic Fluids: A Numerical Study,” Comm. Nonlinear Sci. Numer. Simulat. 16, 711–721 (2011).

    Article  ADS  Google Scholar 

  8. B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces. 1. Boundary Layer Equations for Two Dimensional and Axisymmetric Flow,” AIChE. J. 7, 26–28 (1961).

    Article  Google Scholar 

  9. L. J. Crane, “Flow Past a Stretching Plate,” Z. Angew. Math. Phys. 21, 645–647 (1970).

    Article  Google Scholar 

  10. G. M. A. Rahman, “Thermal-Diffusion and MHD for Soret and Dufour’s Effects on Hiemenz Flow and Mass Transfer of Fluid Flow through Porous Medium onto a Stretching Surface,” Physica B 405, 2560–2569 (2010).

    Article  ADS  Google Scholar 

  11. T. Fang, J. Zhang, and S. Yao, “A New Family of Unsteady Boundary Layers over a Stretching Surface,” Appl. Math. Comput. 217, 3747–3755 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  12. A. Ahmad and S. Asghar, “Flow of a Second Grade Fluid over a Sheet Stretching with Arbitrary Velocities Subject to a Transverse Magnetic Field,” Appl. Math. Lett. 24, 1905–1909 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  13. B. Yao and J. Chen, “Series Solution to the Falkner–Skan Equation with Stretching Boundary,” Appl. Math. Comput. 208, 156–164 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  14. A. A. Joneidi, G. Domairry, and M. Babaelahi, “Analytical Treatment of MHD Free Convective Flow and Mass Transfer over a Stretching Sheet with Chemical Reaction,” J. Taiwan Inst. Chem. Eng. 41, 35–43 (2010).

    Article  MATH  Google Scholar 

  15. R. Kandasamy, and I. Hashim, “Effect of Chemical Reaction, Heat and Mass Transfer on Nonlinear Boundary Layer Past a Porous Shrinking Sheet in the Presence of Suction,” Nuclear Eng. Design 240, 933–939 (2010).

    Article  Google Scholar 

  16. T. Hayat, M. Qasim, and Z. Abbas, “Radiation and Mass Transfer Effects on the Magnetohydrodynamic Unsteady Flow Induced by a Stretching Sheet,” Z. Naturforsch., Ser. A 64, 231–239 (2010).

    ADS  Google Scholar 

  17. T. Hayat, S. A. Shehzad, and M. Qasim, “Mixed Convection Flow of a Micropolar Fluid with Radiation and Chemical Reaction,” Int. J. Numer. Methods Fluids 67, 2375–2387 (2011).

    MathSciNet  MATH  Google Scholar 

  18. R. Md. Kasmani, I. Muhaimin, and R. Kandasamy, “Laminar Boundary Layer Flow of a Nanofluid along a Wedge in the Presence of Suction/Injection,” J. Appl. Mech. Tech. Phys. 54 (3), 377–384 (2013).

    Article  ADS  MATH  Google Scholar 

  19. P. S. Gupta and A. S. Gupta, “Heat and Mass Transfer on a Stretching Sheet with Suction and Blowing,” Canad. J. Chem. Eng. 55, 744–746 (1977).

    Article  Google Scholar 

  20. E. M. A. Elbashbeshy, “Heat Transfer over an Exponentially Stretching Continuous Surface with Suction,” Arch. Mech. 53, 643–651 (2001).

    MATH  Google Scholar 

  21. M. K. Partha, P. V. S. N.Murthy, and G. P. Rajasekhar, “Effects of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface,” Heat Mass Transfer 41, 360–366 (2005).

    Article  ADS  Google Scholar 

  22. M. Sajid and T. Hayat, “Influence of Thermal Radiation on the Boundary Layer Flow Due to an Exponentially Stretching Sheet,” Int. Comm. Heat Mass Transfer 35, 347–356 (2008).

    Article  Google Scholar 

  23. S. K. Khan, “Boundary Layer Viscoelastic Fluid Flow over an Exponentially Stretching Sheet,” Int. J. Appl. Mech. Eng. 11, 321–335 (2006).

    MATH  Google Scholar 

  24. S. K. Khan and E. Sanjayanand, “Viscoelastic Boundary Layer Flow and Heat Transfer over an Exponential Stretching Sheet,” Int. J. Heat Mass Transfer 48, 1534–1542 (2005).

    Article  MATH  Google Scholar 

  25. B. Bidin and R. Nazar, “Numerical Solution of the Boundary Layer Flow over an Exponentially Stretching Sheet with Thermal Radiation,” Europ. J. Sci. Res. 33, 710–717 (2009).

    Google Scholar 

  26. D. Pal, “Mixed Convection Heat Transfer in the Boundary Layers on an Exponentially Stretching Surface with Magnetic Field,” Appl. Math. Comput. 217, 2356–2369 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  27. B. Sahoo and S. Poncet, “Flow and Heat Transfer of a Third Grade Fluid Past an Exponentially Stretching Sheet with Partial Slip Boundary Condition,” Int. J. Heat Mass Transfer 54, 5010–5019 (2011).

    Article  MATH  Google Scholar 

  28. S. Mukhopadhyay, M. Golam Arif, and M. Wazed Ali, “Effects of Partial Slip on Chemically Reactive Solute Transfer in the Boundary Layer Flow over an Exponentially Stretching Sheet with Suction/Blowing,” J. Appl. Mech. Tech. Phys. 54 (6), 928–936 (2013).

    Article  ADS  Google Scholar 

  29. S. J. Liao, Beyond Perturbation: Introduction to Homotopy Analysis Method (Chapman and Hall–CRC Press, Boca Raton, 2003).

    Book  Google Scholar 

  30. M. M. Rashidi and S. A. M. Pour, “Analytic Approximate Solutions for Unsteady Boundary-Layer Flow and Heat Transfer due to a Stretching Sheet by Homotopy Analysis Method,” Nonlinear Anal. Model. Control. 15, 83–95 (2010).

    MathSciNet  MATH  Google Scholar 

  31. R. Kandasamy and I. Muhaimin, “Homotopy Analysis Method for Thermophoretic Particle Deposition Effect on Magnetohydrodynamic Mixed Convective Heat and Mass Transfer Past a Porous Wedge in the Presence of Suction,” J. Appl. Mech. Tech. Phys. 51, (2), 249–260 (2010).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. H. Tabaei, M. A. Moghimi, A. Kimiaeifar, and M. A. Moghimi, “Homotopy Analysis and Differential Quadrature Solution of the Problem of Free-Convective Magnetohydrodynamic Flow over a Stretching Sheet with the Hall Effect and Mass Transfer Taken into Account,” J. Appl. Mech. Tech. Phys. 52 (4), 624–636 (2011).

    Article  ADS  MATH  Google Scholar 

  33. Z. Ziabakhsh, G. Domairry, H. Bararnia, and H. Babazadeh, “Analytical Solution of Flow and Diffusion of Chemically Reactive Species over a Nonlinearly Stretching Sheet Immersed in a Porous Medium,” J. Taiwan Inst. Chem. Eng. 41, 22–28 (2010).

    Article  Google Scholar 

  34. M. Turkyilmazoglu, “Solution of the Thomas–Fermi Equation with a Convergent Approach,” Comm. Nonlinear Sci. Numer. Simulat. 17, 4097–4103 (2012).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. S. Abbasbandy and A. Shirzadi, “Homotopy Analysis Method for a Nonlinear Chemistry Problem,” Studies Nonlinear Sci. 1, 127–132 (2010).

    MATH  Google Scholar 

  36. S. A. Shehzad, A. Alsaedi, and T. Hayat, “Hydromagnetic Steady Flow of Maxwell Fluid over a Bidirectional Stretching Surface with Prescribed Surface Temperature and Prescribed Surface Heat Flux,” Plos One 8, e68139 (2013).

    Article  ADS  Google Scholar 

  37. T. Hayat, M. Waqas, S. A. Shehzad, and A. Alsaedi, “Mixed Convection Radiative Flow of Maxwell Fluid Near a Stagnation Point with Convective Condition,” J. Mech. 29, 403–409 (2013).

    Article  Google Scholar 

  38. F. E. Alsaadi, S. A. Shehzad, T. Hayat, and S. J. Monaquel, “Soret and Dufour Effects on the Unsteady Mixed Convection Flow over a Stretching Surface,” J. Mech. 29, 623–632 (2013).

    Article  Google Scholar 

  39. A. Moradi, H. Ahmadikia, T. Hayat, and A. Alsaedi, “On Mixed Convection Radiation Interaction about an Inclined Plate through a Porous Medium,” Int. J. Thermal Sci. 64, 129–136 (2013).

    Article  Google Scholar 

  40. S. Sadri and M. Babaelahi, “Analysis of Laminar Boundary Layer Flow over a Flat Plate with Injection or Suction,” J. Appl. Mech. Tech. Phys. 54 (1), 59–67 (2013).

    Article  ADS  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, COMSATS Institute of Information Technology, Sahiwal, 57000, Pakistan

    S. A. Shehzad

  2. Department of Mathematics, Quaid-i-Azam University 45320, Islamabad, 44000, Pakistan

    T. Hayat

  3. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, 21589, Saudi Arabia

    T. Hayat & A. Alsaedi

Authors
  1. S. A. Shehzad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Hayat
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Alsaedi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. A. Shehzad.

Additional information

Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 57, No. 4, pp. 114–124, July–August, 2016.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shehzad, S.A., Hayat, T. & Alsaedi, A. Flow of a thixotropic fluid over an exponentially stretching sheet with heat transfer. J Appl Mech Tech Phy 57, 672–680 (2016). https://doi.org/10.1134/S0021894416040118

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0021894416040118

Keywords

Search

Navigation