Reconstruction of Electron-Density Height Profiles Based in the Bottomside Ionosphere on Topside Satellite Sounding Data with the IRI Model

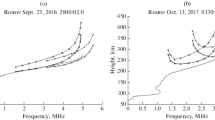
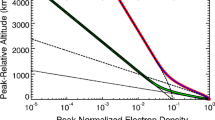
Abstract

A method is proposed to determine the total height profiles of the electron density in the ionosphere with the use of topside satellite ionograms containing traces of sounding signal reflections from the Earth’s surface. The monotonic profile from the satellite to a certain height hm above the height hmF2 of the F2-layer maximum is calculated with the classical method based on reflections from the topside ionosphere. Below the height hm, down to the ionospheric base, the profile is represented by a system of interrelated analytical functions with a limited number of parameters. Their values are found with optimization methods and the joint use of traces of signal reflections, both from the outer part of the ionosphere and from the Earth. To increase the stability of the problem, the lower part of the sought profile in the E region is specified by an unchangeable profile from the IRI-2016 model. The method reliably determines the parameters of the hmF2 maximum, NmF2, and the profile in its vicinity. The addition of key parameters—hmF2, NmF2, and the additionally calculated values B0 and B1, which determine the profile shape in the F region—to the IRI model makes it possible to obtain an IRI profile that is corrected for the actual experimental conditions. The calculated and corrected profiles are similar in the bottomside ionosphere and can noticeably differ in the topside ionosphere. Thus, the use of this proposed method for the reconstruction of the total height profile of the electron density expands the informational value of topside satellite sounding of the ionosphere.

APPENDIX

1.1 7.1. Group Refractive Index of Extraordinary Waves

We used expressions from Paul (1967):

$${{\mu }}_{x}^{'}\left( {f,{{f}_{N}}} \right) = \frac{{{{M}_{x}}\left( X \right)}}{{\sqrt {1 - \tilde {X}} }},$$

$$\begin{gathered} {{M}_{x}}\left( X \right) = \sqrt {\frac{{1 + P{{\cos\theta }}}}{{1 - Y}}\frac{{P - Y{{\cos\theta }}}}{{P + {{\cos\theta }}}}} \\ \times \,\,\left[ {1 + X\frac{{{{{{\cos}}}^{2}}{{\theta }}}}{{{{{{\sin}}}^{2}}{{\theta }}}}\frac{{1 - {{P}^{2}}}}{{1 + {{P}^{2}}}}\frac{{1 - X{{P}^{2}}}}{{{{{\left( {P - Y{{\cos\theta }}} \right)}}^{2}}}}} \right], \\ \end{gathered} $$

$$\begin{gathered} P = \frac{{2\frac{{1 - X}}{Y}\frac{{{{\cos\theta }}}}{{{{{{\sin}}}^{2}}{{\theta }}}}}}{{1 + \sqrt {1 + {{{\left( {2\frac{{1 - X}}{Y}\frac{{{{\cos\theta }}}}{{{{{{\sin}}}^{2}}{{\theta }}}}} \right)}}^{2}}} }}~,\,\,\,\,~Y = \frac{{{{f}_{H}}}}{f}~,~ \\ ~X = ~\frac{{f_{N}^{2}}}{{{{f}^{2}}}}~,~\,\,\,\,~\tilde {X} = ~\frac{X}{{1 - Y~}}~. \\ \end{gathered} $$

Here, f_H is the electron gyrofrequency, and θ is the angle between the wave vector (vertical) and vector of the geomagnetic field strength.

1.2 7.2. Matrix Elements for the Exponential Profile

Let

$$\begin{gathered} f_{N}^{2}\left( h \right) = f_{{N1}}^{2}{\text{exp}}\left( { - \frac{{h - {{h}_{1}}}}{H}} \right),~\,\,\,\,~{{h}_{1}} \leqslant h \leqslant {{h}_{2}}, \\ {{f}_{{N1}}} \geqslant {{f}_{N}} \geqslant {{f}_{{N2}}}. \\ \end{gathered} $$

In dimensionless variables,

$$\begin{gathered} \tilde {X}\left( h \right) = {{{\tilde {X}}}_{1}}{\text{exp}}\left( { - \frac{{h - {{h}_{1}}}}{H}} \right),\,\,\,~{{{\tilde {X}}}_{1}} = \frac{{{{X}_{1}}}}{{1 - Y}},~ \\ {{{\tilde {X}}}_{2}} = \frac{{{{X}_{2}}}}{{1 - Y}}. \\ \end{gathered} $$

The group path in these variables is

$$\begin{gathered} {{\Delta }}P_{x}^{'}\left( f \right) = \mathop \smallint \limits_{{{h}_{1}}}^{{{h}_{2}}} {{\mu }}_{x}^{'}\left[ {f,{{f}_{N}}\left( h \right)} \right]dh \\ = \mathop \smallint \limits_{{{{\tilde {X}}}_{1}}}^{{{{\tilde {X}}}_{2}}} \frac{{{{M}_{x}}\left[ {\tilde {X}\left( {1 - Y} \right)} \right]}}{{\sqrt {1 - \tilde {X}} }}\frac{{dh}}{{d\tilde {X}}}d\tilde {X}. \\ \end{gathered} $$

Taking into account that

$$\frac{{dh}}{{d\tilde {X}}} = - \frac{H}{{\tilde {X}}},$$

we obtain

$${{\Delta }}P_{x}^{'}\left( f \right) = - H\mathop \smallint \limits_{{{{\tilde {X}}}_{1}}}^{{{{\tilde {X}}}_{2}}} \frac{{{{M}_{x}}\left[ {\tilde {X}\left( {1 - Y} \right)} \right]}}{{\sqrt {1 - \tilde {X}} }}\frac{{d\tilde {X}}}{{\tilde {X}}}.$$

Making the change of variables $\tilde {X} = 1 - {{t}^{2}},~$ we find

$$\begin{gathered} {{\Delta }}P_{x}^{'}\left( f \right) = 2H\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} \frac{{{{M}_{x}}\left[ {\left( {1 - {{t}^{2}}} \right)\left( {1 - Y} \right)} \right]}}{{1 - {{t}^{2}}}}~dt = HM\left( f \right), \\ {{t}_{1}} = \sqrt {1 - {{{\tilde {X}}}_{1}}} ~,\,\,\,\,~{{t}_{2}} = \sqrt {1 - {{{\tilde {X}}}_{2}}} ~, \\ \end{gathered} $$

where M(f) is the matrix element of the exponential profile.

1.3 7.3. Matrix Elements for the Quasi-Gaussian Profile

Let

$$\begin{gathered} f_{N}^{2}\left( h \right) = f_{{\text{c}}}^{2}{\text{exp}}\left[ { - {{{\left( {\frac{{{{h}_{{{\text{max}}}}} - h}}{H}} \right)}}^{2}}} \right],~ \\ ~\tilde {X}\left( h \right) = {{{\tilde {X}}}_{{\text{c}}}}{\text{exp}}\left[ { - {{{\left( {\frac{{{{h}_{{{\text{max}}}}} - h}}{H}} \right)}}^{2}}} \right],~ \\ {{{\tilde {X}}}_{{\text{c}}}} = \frac{{{{X}_{{\text{c}}}}}}{{1 - Y}},~\,\,\,\,{{X}_{{\text{c}}}} = \frac{{f_{{\text{c}}}^{2}}}{{{{f}^{2}}}}. \\ \end{gathered} $$

Taking into account that

$$\frac{{dh}}{{d\tilde {X}}} = \,\,~{H \mathord{\left/ {\vphantom {H {\left( {2\tilde {X}\sqrt {{\text{ln}}\left( {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}}}} \right. \kern-0em} {\tilde {X}}}} \right)} } \right)}}} \right. \kern-0em} {\left( {2\tilde {X}\sqrt {{\text{ln}}\left( {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}}}} \right. \kern-0em} {\tilde {X}}}} \right)} } \right)}},$$

we obtain in new variables

$${{\Delta }}P_{x}^{'}\left( f \right) = \frac{H}{2}\mathop \smallint \limits_{{{{\tilde {X}}}_{1}}}^{{{{\tilde {X}}}_{2}}} \frac{{{{M}_{x}}\left[ {\tilde {X}\left( {1 - Y} \right)} \right]}}{{\sqrt {1 - \tilde {X}} }}{{d\tilde {X}} \mathord{\left/ {\vphantom {{d\tilde {X}} {\left( {\tilde {X}\sqrt {{\text{ln}}\left( {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}}}} \right. \kern-0em} {\tilde {X}}}} \right)} } \right)}}} \right. \kern-0em} {\left( {\tilde {X}\sqrt {{\text{ln}}\left( {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}}}} \right. \kern-0em} {\tilde {X}}}} \right)} } \right)}}.$$

Making the change of variables $\tilde {X} = 1 - {{t}^{2}},$ we find

$$\begin{gathered} {{\Delta }}P_{x}^{'}\left( f \right) = H\mathop \smallint \limits_{{{t}_{2}}}^{{{t}_{1}}} \frac{{{{M}_{x}}\left[ {\left( {1 - {{t}^{2}}} \right)\left( {1 - Y} \right)} \right]}}{{\tilde {X}\left( t \right)\sqrt {{\text{ln}}\left[ {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}\left( t \right)}}} \right. \kern-0em} {\tilde {X}\left( t \right)}}} \right]} }}dt,~ \\ {{t}_{1}} = \sqrt {1 - {{{\tilde {X}}}_{1}}} ,\,\,\,\,~~{{t}_{2}} = \sqrt {1 - {{{\tilde {X}}}_{2}}} . \\ \end{gathered} $$

For signals reflected by the topside ionosphere,

$$\begin{gathered} {{t}_{{{\text{2top}}}}} = 0,\,\,\,\,~~{{t}_{{{\text{1top}}}}} = \sqrt {1 - {{{\tilde {X}}}_{{{\text{1top}}}}}} ~,~ \\ {{{\tilde {X}}}_{{{\text{1top}}}}} = {{f_{{Nm}}^{2}} \mathord{\left/ {\vphantom {{f_{{Nm}}^{2}} {\left[ {{{f}^{2}}\left( {1 - Y} \right)} \right]}}} \right. \kern-0em} {\left[ {{{f}^{2}}\left( {1 - Y} \right)} \right]}}, \\ \end{gathered} $$

the matrix element ${{A}_{{{\text{top}}}}}\left( {f,{{f}_{{\text{c}}}}} \right)~$ has the form

$${{A}_{{{\text{top}}}}}\left( {f,{{f}_{{\text{c}}}}} \right) = \mathop \smallint \limits_0^{{{t}_{{1t{\text{op}}}}}} \frac{{{{M}_{x}}\left[ {\left( {1 - {{t}^{2}}} \right)\left( {1 - Y} \right)} \right]}}{{\tilde {X}\left( t \right)\sqrt {\ln \left[ {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}\left( t \right)}}} \right. \kern-0em} {\tilde {X}\left( t \right)}}} \right]} }}dt.$$

For signals reflected by the Earth’s surface,

$$\begin{gathered} {{A}_{1}}\left( {f,{{f}_{{\text{c}}}}} \right) = \mathop \smallint \limits_{{{t}_{2}}}^{{{t}_{1}}} \frac{{{{M}_{x}}\left[ {\left( {1 - {{t}^{2}}} \right)\left( {1 - Y} \right)} \right]}}{{\tilde {X}\left( t \right)\sqrt {{\text{ln}}\left[ {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}\left( t \right)}}} \right. \kern-0em} {\tilde {X}\left( t \right)}}} \right]} }}dt, \\ ~{{t}_{1}} = \sqrt {1 - {{{\tilde {X}}}_{{{\text{1top}}}}}} ,\,\,\,\,~{{t}_{2}} = \sqrt {1 - {{{\tilde {X}}}_{{\text{c}}}};} \\ \end{gathered} $$

for the height interval h_max ≤ h ≤ hm in the topside ionosphere. For the height interval in the bottomside ionosphere h_B ≤ h ≤ h_max,

$$\begin{gathered} {{A}_{2}}\left( {f,{{f}_{{\text{c}}}}} \right) = \int\limits_{{{t}_{2}}}^{{{t}_{1}}} {\frac{{{{M}_{x}}\left[ {\left( {1 - {{t}^{2}}} \right)\left( {1 - Y} \right)} \right]}}{{\tilde {X}\left( t \right)\sqrt {{\text{ln}}\left[ {{{{{{\tilde {X}}}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{{\tilde {X}}}_{{\text{c}}}}} {\tilde {X}\left( t \right)}}} \right. \kern-0em} {\tilde {X}\left( t \right)}}} \right]} }}} dt,~ \\ {{t}_{1}} = \sqrt {1 - {{{\tilde {X}}}_{{1B}}}} ,~\,\,\,\,{{t}_{2}} = \sqrt {1 - {{{\tilde {X}}}_{{\text{c}}}};} \\ \end{gathered} $$

$${{\tilde {X}}_{{1B}}} = {{f_{B}^{2}} \mathord{\left/ {\vphantom {{f_{B}^{2}} {\left[ {{{f}^{2}}\left( {1 - Y} \right)} \right]}}} \right. \kern-0em} {\left[ {{{f}^{2}}\left( {1 - Y} \right)} \right]}}.$$

1.4 7.4. Matrix Elements for the Parabolic Profile

Let

$${{f}_{N}}\left( h \right) = {{f}_{v}} + \left( {{{f}_{B}} - {{f}_{v}}} \right){{\left( {\frac{{h - {{h}_{v}}}}{{{{h}_{B}} - {{h}_{v}}}}} \right)}^{2}},~\,\,\,\,{{h}_{v}} < h \leqslant {{h}_{B}}.$$

The contribution to group paths is

$$\begin{gathered} {{\Delta }}P_{x}^{'}\left( f \right) = \int\limits_{{{h}_{v}}}^{{{h}_{{{\text{max}}}}}} {{{\mu }}_{x}^{'}\left[ {f,{{f}_{N}}\left( h \right)} \right]dh} \\ = \int\limits_{{{f}_{v}}}^{{{f}_{B}}} {{{\mu }}_{x}^{'}\left[ {f,{{f}_{N}}} \right]} \frac{{dh}}{{d{{f}_{N}}}}~d{{f}_{N}}. \\ \end{gathered} $$

Let us find the derivative

$$\frac{{dh}}{{d{{f}_{N}}}} = \frac{{{{h}_{B}} - {{h}_{v}}}}{{2\sqrt {\left( {{{f}_{B}} - {{f}_{v}}} \right)\left( {{{f}_{N}} - {{f}_{v}}} \right)} }}$$

and substitute into the expression for ${{\Delta }}P_{x}^{'}\left( f \right)$:

$${{\Delta }}P_{x}^{'}\left( f \right) = \frac{{{{h}_{B}} - {{h}_{v}}}}{{2\sqrt {{{f}_{B}} - {{f}_{v}}} }}\int\limits_{{{f}_{v}}}^{{{f}_{B}}} {{{\mu }}_{x}^{'}\left[ {f,{{f}_{N}}} \right]} \frac{{~d{{f}_{N}}}}{{\sqrt {{{f}_{N}} - {{f}_{v}}} }}.$$

Replacing the integration variable as ${{f}_{N}} = {{f}_{v}}\left( {1 + {{t}^{2}}} \right)$, we obtain

$$\begin{gathered} {{\Delta }}{{P}_{{gx}}}\left( f \right) = \left( {{{h}_{B}} - {{h}_{v}}} \right)\sqrt {\frac{{{{f}_{v}}}}{{{{f}_{B}} - {{f}_{v}}}}} \int\limits_{{{t}_{v}}}^{{{t}_{B}}} {{{\mu }}_{x}^{'}\left[ {f,{{f}_{N}}\left( t \right)} \right]dt} , \\ ~{{t}_{v}} = 0,~\,\,\,~{{t}_{B}} = \sqrt {\frac{{{{f}_{B}}}}{{{{f}_{v}}}} - 1} . \\ \end{gathered} $$

Thus, the expression for matrix elements ${{A}_{{vB}}}\left( f \right)$ takes the form

$${{A}_{{vB}}}\left( f \right) = \sqrt {\frac{{{{f}_{v}}}}{{{{f}_{B}} - {{f}_{v}}}}} \int\limits_0^{{{t}_{B}}} {{{\mu }}_{x}^{'}\left[ {f,{{f}_{N}}\left( t \right)} \right]} dt.$$