Abstract—
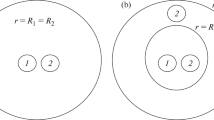
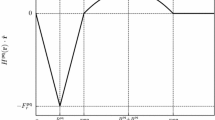
In aggregates formed by cells of different types, the phenomenon of their sorting is observed: as a result of cell interactions, structures develop in which cells of one type can form a compact mass surrounded by cells of another type. The physical mechanisms underlying the sorting process are still the subject of discussion. We have previously proposed a continuum model of a biological continuum formed by two actively interacting cell phases and a fluid. Based on this model, a model problem of redistribution of cells of two types, which fill an infinite plane layer, was considered under the assumption that the continuums modeling two cell populations are bounded by a common outer boundary. In the proposed study, a similar problem is formulated and investigated, taking into account the possible relative displacement of surfaces that bound cells of different types. This formulation allows us to describe the formation and propagation of fronts separating regions that differ in the concentrations of cell phases. The behavior of solutions is studied depending on the dimensionless parameters characterizing active intercellular interactions. The participation of these mechanisms in the formation of new cellular structures was analyzed numerically. It has been shown that, in a wide range of parameters, cells with stronger contracting active interactions tend to occupy the central region, displacing cells with weaker contracting interactions to the periphery. The novel formulation is physically more adequate and allows us to expand the range of parameters in which a stable result is achieved.




Similar content being viewed by others
REFERENCES
Beloussov, L.V., Dorfman, J.G., and Cherdantzev V.G., Mechanical stresses and morphological patterns in amphibian embryos, J. Embr. Exp. Morphol., 1975, vol. 34, pp. 559–574.
Keller, R., Davidson, L.A., and Shook, D.R., How we are shaped: The biomechanics of gastrulation, Differentiation, 2003, vol. 71, pp. 171–205.
Mammoto, T. and Ingber, D.E., Mechanical control of tissue and organ development, Development, 2010, vol. 137, no. 9, pp. 1407–1420.
Steinberg, M.S. and Wiseman, L.L., Do morphogenetic tissue rearrangements require active cell movements? J. Cell Biol., 1972, vol. 55, pp. 606–615.
Foty, R.A. and Steinberg, M.S., Cadherin-mediated cell-cell adhesion and tissue segregation in relation to malignancy, Int. J. Dev. Biol., 2004, vol. 48, pp. 397–409.
Mehes, E. and Viscek, T., Segregation mechanisms of tissue cells: from experimental data to models, Complex Adapt. Syst. Model., 2013, vol. 1, p. 4.
Mehes, E. and Viscek, T., Collective motion of cells: from experiments to models, Integr. Biol., 2014, vol. 6, no. 9, pp. 831–854.
Graner, F. and Glazier, J.A., Simulation of biological cell sorting using a two-dimensional extended Potts model, Phys. Rev. Lett., 1992, vol. 69, pp. 2013–2016.
Glazier, J.A. and Graner, F., Simulation of the differential adhesion driven rearrangement of biological cells, Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics, 1993, vol. 47, pp. 2128–2154.
Krieg, M., Arboleda-Estudillo, Y., Puech, P.H., et al., Tensile forces govern germ-layer organization in zebrafish, Nat. Cell Biol., 2008, vol. 10, pp. 429–436.
Zhang, Y., Thomas, G.L., Swat, M., et al., Computer simulations of cell sorting due to differential adhesion, PLoS One, 2011, vol. 6, p. e24999.
Brodland, G.W. and Chen, H.H., The mechanics of heterotypic cell aggregates: insights from computer simulations, J. Biomech. Eng., 2000, vol. 122, pp. 402–407.
Brodland, G.W., The differential interfacial tension hypothesis (DITH): a comprehensive theory for the self-rearrangement of embryonic cells and tissues, J. Biomech. Eng., 2002, vol. 124, pp. 188–197.
Fletcher, A.G., Osborne, J.M., Maini, P.K., and Gavaghan, D.J., Implementing vertex dynamics models of cell populations in biology within a consistent computational framework,” Prog. Biophys. Mol. Biol., 2013, vol. 113, pp. 299–326.
Katsunuma, S., Honda, H., Shinoda, T., et al., Synergistic action of nectins and cadherins generates the mosaic cellular pattern of the olfactory epithelium, J. Cell Biol., 2016, vol. 212, pp. 561–575.
Tanaka, S., Simulation frameworks for morphogenetic problems, Computation, 2015, vol. 3, pp. 197–221.
Osborne, J.M., Fletcher, A.G., Pitt-Francis, J.M., et al., Comparing individual-based approaches to modelling the self-organization of multicellular tissues, PLoS Comput. Biol., 2017, vol. 13, p. e1005387.
Camley, B.A. and Rappel, W.J., Physical models of collective cell motility: from cell to tissue, J. Phys. D Appl. Phys., 2017, vol. 50, p. 113002.
Armstrong, N.J., Painter, K.J., and Sherratt, J.A., A continuum approach to modelling cell-cell adhesion, J. Theor. Biol., 2006, vol. 243, no. 1, pp. 98–113.
Painter, K.J., Bloomfield, J.M., Sherratt, J.A., and Gerisch, A., A nonlocal model for contact attraction and repulsion in heterogeneous cell populations, Bull. Math. Biol., 2015, vol. 77, pp. 1132–1165.
Murakawa, H. and Togashi, H., Continuous models for cell–cell adhesion, J. Theor. Biol., 2015, vol. 374, pp. 1–12.
Carrillo, J.A., Murakawa, H., Sato, M., et al. A population dynamics model of cell-cell adhesion incorporating population pressure and density saturation, J. Theor. Biol., 2019, vol. 474, pp. 14–24.
Stein, A.A., Logvenkov, S.A., and Volodyaev, I.V., Continuum modeling of mechano-dependent reactions in tissues composed of mechanically active cells, BioSystems, 2018, vol. 173, pp. 225–234.
Logvenkov, S.A. and Stein, A.A., Continuum modeling of the biological medium composed of actively interacting cells of two different types, Fluid Dynamics, 2020, vol. 55, no. 6, pp. 721–734.
Beloussov, L.V., Logvenkov, S.A., and Stein, A.A., Mathematical model of an active biological continuous medium with account for the deformations and rearrangements of the cells, Fluid Dynamics, 2015, vol. 50, no. 1, pp. 1–9.
Korn, G.A. and Korn T.M., Mathematical Handbook for Scientists and Engineers (McGraw-Hill, New York et al., 1968).
Samarskii, A.A., The Theory of Difference Schemes (Nauka, Moscow, 1977) [in Russian].
Harten, A., High resolution schemes for hyperbolic conservation laws, J. Comput. Phys., 1983, vol. 49, no. 3, pp. 357–393.
Chirkov, D.V. and Chernyi, S.G., Comparison of accuracy and convergence of some TVD schemes, Vychislitelnye Tekhnologii, 2000, vol. 5, no. 5, pp. 86–107.
Funding
The study was supported financially by the Russian Foundation for Basic Research (project no. 20-01-00329) and the State Program АААА-А19-119012990119-3.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
The authors declare no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Rights and permissions
About this article
Cite this article
Logvenkov, S.A., Stein, A.A. Continuum Modeling of Cell Sorting within a Plane Layer with Account for the Possible Separation of the Boundaries of the Regions Occupied by Cells of Two Different Types. Fluid Dyn 57, 221–233 (2022). https://doi.org/10.1134/S0015462822030090
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0015462822030090