Abstract
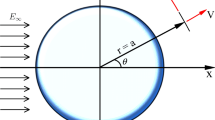
—The motion of a charged dielectric microparticle in an electric field is first studied over a wide parameter range on the base of the numerical solution of the system of Nernst–Planck–Poisson–Stokes equations. As the most important result, the formation of microvortices on the rear side of the particle is revealed. The microvortices lose their steadiness with increase in the electric field strength and separate periodically from the particle surface. Separation becomes chaotic with further increase in the electric field strength. The phenomenon strongly resembles the formation of the Kármán street but it has another physical mechanism by virtue of almost zero Reynolds numbers of micro- and nanoparticle flow. The asymptotic analysis is carried out and the mechanism of microvortex formation and separation is theoretically substantiated at small Debye numbers.




Similar content being viewed by others
REFERENCES
Smoluchowski, M., Contribution to the theory of electro-osmosis and related phenomena, Bull. Int. Acad. Sci. Cracovie, 1903, vol. 184, p. 199.
Napoli, M., Eijkel, J.C.T., and Pennathur, S., Nanofluidic technology for biomolecule applications, Lab. Chip., 2010, vol. 10, p. 957.
Chang, H.-C., Yossifon, G., and Demekhin, E.A., Nanoscale electrokinetics and microvortices, Annu. Rev. Fluid Mech., 2012, vol. 44, p. 401.
Granick, S. and Jiang, S., Janus Particle Synthesis, Self-Assembly and Applications, The Royal Society of Chemistry, 2012.
Schnitzer, O. and Yariv, E., Macroscale description of electrokinetic flows at large zeta potentials: Nonlinear surface conduction, Phys. Rev. E, 2012, vol. 86, no. 2, p. 021503.
Schnitzer, O., Zeyde, R., Yavneh, I., and Yariv, E., Weakly nonlinear electrophoresis of a highly charged colloidal particle, Physics of Fluids, 2013, vol. 25, no. 5, p. 052004.
Schnitzer, O. and Yariv, E., Nonlinear electrophoresis at arbitrary field strengths: small-Dukhin-number analysis, Physics of Fluids, 2014, vol. 26, no. 12, p. 122002.
Tottori, S., Misiunas, K., and Keyser, U.F., Nonlinear electrophoresis of highly charged nonpolarizable particles, Physical Review Letters, 2019, vol. 123, no. 1, p. 014502.
Mishchuk, N.A. and Takhistov, P.V., Electroosmosis of the second kind, Colloids and Surfaces A, 1995, vol. 95, p. 119.
Ben, Y., Demekhin, E.A., and Chang, H.-C., Nonlinear electrokinetics and “superfast” electrophoresis, J. Colloid Interface Sci., 2004, vol. 276, p. 483.
Ganchenko, G., Frants, E., Shelistov, V., Nikitin, N., Amiroudine, S., and Demekhin, E., Extreme nonequilibrium electrophoresis of an ion-selective microgranule, Physical Review Fluids, 2019, vol. 4, no.4, p. 043703.
Vázquez, P.A., Pérez, A.T., Castellanos, A., and Atten, P., Dynamics of electrohydrodynamic laminar plumes: Scaling analysis and integral model, Phys. Fluids, 2000, vol. 12, no. 11, p. 2809.
Nikitin, N.V., Third-order-accurate semi-implicit Runge-Kutta scheme for incompressible Navier–Stokes equations, Int. J. Numer. Meth. Fluids, 2006, vol. 51, pp. 221–233.
Van Dyke, M., Perturbation Methods in Fluid Mechanics, New York: Academic Press, 1964.
Probstein, R.F. Physicochemical Hydrodynamics. An Introduction, New York: Wiley-Interscience, 2005.
Suetin, P.K., Klassicheskie ortogonal’nye mnogochleny (Classical Orthogonal Polynomials), Moscow: Fizmatgiz, 2007.
Gary Leal, L., Laminar Flow and Convective Transport Processes: Scaling Principles and Asymptotic Analysis, Butterworth-Heinemann, 1992.
ACKNOWLEGMENTS
The authors are very grateful to Prof. V.A. Polyanskii (Moscow State University) for his remarks on formulation of the problem, discussion and analysis of the calculation results, and indication to certain important studies unknown to the authors. Finally, all this was favorable to significant improvement in the quality of the paper. The work was carried out using the equipment of the Center of shared research facilities of HP computing resources at Lomonosov Moscow State University.
Funding
The work was carried out with financial support from the Russian Foundation for Basic Research and the Administration of the Krasnodar Territory (project no. 19-48-235001).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by E.A. Pushkar
Rights and permissions
About this article
Cite this article
Frants, E.A., Artyukhov, D.A., Kireeva, T.S. et al. Vortex Formation and Separation from the Surface of a Charged Dielectric Microparticle in a Strong Electric Field. Fluid Dyn 56, 134–141 (2021). https://doi.org/10.1134/S0015462821010043
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0015462821010043