Abstract
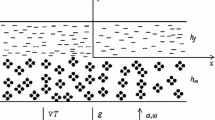
The onset of convection in a system of two horizontal layers (a pure liquid and a porous medium saturated with the same liquid) heated from below under the action of vertical vibration is investigated. For describing the free thermal convection, in the liquid layer the Boussinesq approximation and in the porous layer the Darcy-Boussinesq approximation are used. In the limiting case of a thin liquid layer, effective boundary conditions on the upper boundary of the porous layer with account for convection in the liquid layer are obtained and it is shown that vibration has a stabilizing effect, whereas the presence of a liquid layer leads to destabilization. For an arbitrary liquid to porous layer thickness ratio the onset of convection is investigated numerically. In the case of a thin liquid layer there are two (short-and long-wave) unstable modes. In the case of thick layers the neutral curves are unimodal. Vibration has a stabilizing effect on perturbations with any wave number but affects short-wave perturbations much more strongly than long-wave ones.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
D.A. Nield and A. Bejan, Convection in Porous Media (Springer-Verlag, New York, 1999).
D.V. Lyubimov and I. D. Muratov, “Convective Instability of a Fluid in a Stratified System,” in Hydrodynamics, Is. 1 (Perm, 1977) [in Russian], 38–46.
F. Chen and C.F. Chen, “Onset of Finger Convection in a Horizontal Porous Layer Underlying a Fluid Layer,” ASME J. Heat Transfer, 110, 403–409 (1988).
S.M. Zenkovskaya, “Effect of High-Frequency Vibration on Convection in a Porous Medium,” Prikl. Mekh. Tekhn. Fiz. 33(5), 83–88 (1992)
S.M. Zenkovskaya and T.N. Rogovenko, “Convection in a Porous Media in a High-Frequency Vibration Field,” Prikl. Mekh. Tekhn. Fiz. 40(3), 22–29 (1999).
G. Bardan and A. Mojtabi, “On the Horton-Rogers-Lapwood Convective Instability with Vertical Vibration,” Phys. Fluids, 12, 2723–2731 (2000).
G.S. Beavers and D.D. Joseph, “Boundary Conditions at a Naturally Permeable Wall,” J. Fluid Mech.30, 197–207 (1967).
G.I. Taylor, A Model for the Boundary Condition of a Porous Material. Pt 1,” J. Fluid Mech. 49, 319–326 (1971).
G. Neale and W. Nader, “Practical Significance of Brinkman’s Extension of Darcy’s Law: Coupled Parallel Flows within a Channel and a Bounding Porous Medium,” Canad. J. Chem. Engng. 52, 475–478 (1974).
M. Sahraoui and M. Kaviany, “Slip and No-Slip Velocity Boundary Conditions at the Interface of Porous, Plain Media,” Int. J. Heat Mass Transfer 35, 927–943 (1992).
G.Z. Gershuni and D.V. Lyubimov, Thermal Vibrational Convection (Wiley, New York, et al., 1998).
G.Z. Gershuni, E.M. Zhukhovitskii, and A.A. Nepomnyashchii, Stability of Convective Flows (Nauka, Moscow, 1989) [in Russian].
D.V. Lyubimov, “Convective Flows under the Influence of High-Frequency Vibrations,” Eur. J. Mechanics, B/Fluids 14(4), 439–458 (1995).
C.W. Horton and F.T. Rogers, “Convection Currents in a Porous Medium,” Appl. Phys, 16, 367–370 (1945).
E.R. Lapwood, “Convection of a Fluid in a Porous Medium,” Proc. Camb. Phil. Soc. 44, 508–521 (1948).
G. Z. Gershuni and E.M. Zhukhovitskii, Convective Stability of an Incompressible Fluid (Nauka, Moscow, 1972) [in Russian].
Additional information
Original Russian Text © D.V. Lyubimov, T.P. Lyubimova, I.D. Muratov, E.A. Shishkina, 2008, published in Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, 2008, Vol. 43, No. 5, pp. 132–3.
Rights and permissions
About this article
Cite this article
Lyubimov, D.V., Lyubimova, T.P., Muratov, I.D. et al. Vibration effect on convection onset in a system consisting of a horizontal pure liquid layer and a layer of liquid-saturated porous medium. Fluid Dyn 43, 789–798 (2008). https://doi.org/10.1134/S001546280805013X
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S001546280805013X