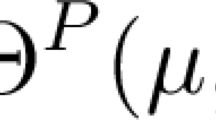Skip to main content
SpringerLink
Log in

Global Algebraic Poincaré–Bendixson Annulus for the van der Pol System

  • ORDINARY DIFFERENTIAL EQUATIONS
  • Published:
Differential Equations Aims and scope Submit manuscript

Abstract

We construct analytically two algebraic closed curves forming a Poincaré–Bendixson annulus for the van der Pol system for all values of its parameter. The inner boundary of the annulus is a closed curve of the zero-level set of a Dulac–Cherkas function, which implies that this annulus contains at most one limit cycle. For the construction of the outer boundary a special procedure is presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

REFERENCES

  1. Sansone, G. and Conti, R., Non-Linear Differential Equations, vol. 67 of Monographs in Pure and Applied Mathematics, Pergamon. 1964.

  2. Dumortier, F., Llibre, L., and Artes, J.C., Qualitative Theory of Planar Differential Systems, Berlin: Springer, 2006.

    MATH  Google Scholar 

  3. Perko, L., Differential Equations and Dynamical Systems, vol. 7 of Texts Appl. Math., Springer, 2001.

  4. Flanders, D.A. and Stoker, J.J., The limit case of relaxation oscillations, in Studies in Nonlinear Vibration Theory, New York: Inst. Math. Mech., New York Univ., 1946, pp. 51–64.

  5. Lynch, S., Dynamical Systems with Applications Using Mathematica, Birkhäuser, 2007.

  6. Schneider, K.R., New approach to study the van der Pol equation for large damping, Electron. J. Qual. Theory Differ. Equat., 2018, no. 8, pp. 1–10.

  7. Giacomini, H. and Grau, M., Transversal conics and the existence of limit cycles, J. Math. Anal. Appl., 2015, vol. 428, pp. 563–586.

    Article  MathSciNet  Google Scholar 

  8. Gasull, A., Giacomini, H., and Grau, M., Effective construction of Poincaré–Bendixson regions, J. Appl. Anal. Comput., 2017, vol. 7, pp. 1549–1569.

    MathSciNet  MATH  Google Scholar 

  9. Cherkas, L.A., Dulac function for polynomial autonomous systems on a plane, Differ. Equations, 1997, vol. 33, no. 5, pp. 689–699.

    MathSciNet  MATH  Google Scholar 

  10. Grin, A.A and Schneider, K.R., On some classes of limit cycles of planar dynamical systems, Dyn. Contin. Discrete Impuls. Syst. Ser. A. Math. Anal., 2007, vol. 14, pp. 641–656.

    MathSciNet  MATH  Google Scholar 

  11. Cherkas, L.A., Grin, A.A., and Schneider, K.R., Dulac–Cherkas functions for generalized Liénard systems, Electron. J. Qual. Theory Differ. Equat., 2011, no. 35, pp. 1–23.

  12. Gasull, A. and Giacomini, H., Upper bounds for the number of limit cycles through linear differential equations, Pac. J. Math., 2006, vol. 226, no. 2, pp. 277–296.

    Article  MathSciNet  Google Scholar 

  13. Gasull, A. and Giacomini, H., Some applications of the extended Bendixson–Dulac theorem, in Progress and Challenges in Dynamical Systems, vol. 54 of Springer Proc. Math. Stat., Heidelberg: Springer, 2013, pp. 233–252.

  14. van der Pol, B., On relaxation-oscillations, London Edinburgh Dublin Phil. Mag. & J. Sci., 1926, vol. 14, pp. 978–992.

    Article  Google Scholar 

Download references

Funding

A.A. Grin acknowledgments the financial support by DAAD as well the hospitality of colleagues from the Technical University in Berlin and the Weierstrass Institute for Applied Analysis and Stochastics in Berlin.

Author information

Authors and Affiliations

  1. Yanka Kupala State University of Grodno, Grodno, 230023, Belarus

    А. А. Grin

  2. Weierstrass Institute for Applied Analysis and Stochastics, Berlin, 10117, Germany

    К. R. Schneider

Authors
  1. А. А. Grin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. К. R. Schneider
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to А. А. Grin or К. R. Schneider.

Additional information

Translated by the Authors

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Grin, А.А., Schneider, К.R. Global Algebraic Poincaré–Bendixson Annulus for the van der Pol System. Diff Equat 58, 285–295 (2022). https://doi.org/10.1134/S0012266122030016

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0012266122030016

Search

Navigation