Skip to main content
SpringerLink
Log in

Theoretical Aspects of Constructing a Neurocontroller for Switched Systems

  • CONTROL THEORY
  • Published:
Differential Equations Aims and scope Submit manuscript

Abstract

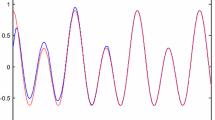
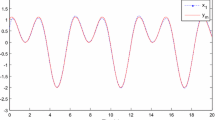
We consider the problem of stabilizing a switched linear system with slow switchings that cannot be observed. The solution is sought in the class of variable structure controllers. To ensure the operability of such a controller, it is necessary to construct a switching signal observer. As an observer, it is proposed to use a neural network. The theoretical aspects of adjusting such an observer are the subject of this paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

REFERENCES

  1. Balandin, D.V. and Kogan, M.M., Sintez zakonov upravleniya na osnove lineinykh matrichnykh neravenstv (Synthesis of Control Laws Based on Linear Matrix Inequalities), Moscow: Fizmatlit, 2007.

    Google Scholar 

  2. Polyak, B.T. and Shcherbakov, P.S., Superstable linear control systems. I. Analysis, Autom. Remote Control, 2002, vol. 63, no. 8, pp. 37–53.

    Article  MathSciNet  MATH  Google Scholar 

  3. Fursov, A.S., Mosolova, Y.M., and Minyaev, S.I., Digital superstabilization of a switched interval linear system, Differ. Equations, 2020, vol. 56, no. 11, pp. 1485–1495.

    Article  MathSciNet  MATH  Google Scholar 

  4. Andreev, Yu.N., Upravlenie konechnomernymi lineinymi ob”ektami (Control of Finite-Dimensional Linear Plants), Moscow: Nauka, 1976.

    MATH  Google Scholar 

  5. Liberzon, D., Switching in Systems and Control, Boston: Springer, 2003.

    Book  MATH  Google Scholar 

  6. Fursov, A.S. and Khusainov, E.F., On the stabilization of switchable linear systems, Differ. Equations, 2015, vol. 51, no. 11, pp. 1518–1528.

    Article  MathSciNet  MATH  Google Scholar 

  7. Fursov, A.S. and Khusainov, E.F., Superstabilization of linear dynamic plants under operator disturbances, Differ. Equations, 2014, vol. 50, no. 7, pp. 854–865.

    Article  MathSciNet  MATH  Google Scholar 

  8. Haykin, S., Neural Networks, Upper Saddle River, NJ: Prentice-Hall, 1999. Translated under the title: Neironnye seti, Moscow: Williams, 2006.

    MATH  Google Scholar 

  9. Demidovich, B.P., Lektsii po matematicheskoi teorii ustoichivosti (Lectures on the Mathematical Theory of Stability), Moscow: Nauka, 1967.

    Google Scholar 

Download references

Funding

This work was supported by the Russian Science Foundation, project no. 22-21-00162.

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Science, Hangzhou Dianzi University, Hangzhou, Zhejiang, 310005, China

    A. S. Fursov

  2. Lomonosov Moscow State University, Moscow, 119991, Russia

    A. S. Fursov & Yu. M. Mosolova

  3. Kharkevich Institute for Information Transmission Problems, Russian Academy of Sciences, Moscow, 127051, Russia

    A. S. Fursov

Authors
  1. A. S. Fursov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu. M. Mosolova
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to A. S. Fursov or Yu. M. Mosolova.

Additional information

Translated by V. Potapchouck

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fursov, A.S., Mosolova, Y.M. Theoretical Aspects of Constructing a Neurocontroller for Switched Systems. Diff Equat 58, 1549–1557 (2022). https://doi.org/10.1134/S00122661220110106

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S00122661220110106

Search

Navigation