Abstract
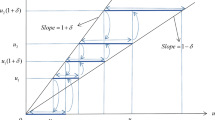
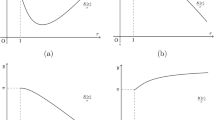
We consider the problem of stabilizing a system of ordinary differential equations nonlinear in the state variables with control parameters. Strict pointwise constraints are imposed on the feasible values of the feedback control. Assuming sufficient smoothness of the functions on the right-hand side in the differential equations, a piecewise affine system is constructed that approximates the original nonlinear system on a rectangular grid in a given state space domain. The stabilizer can also be found in a piecewise affine form; it corresponds to a continuous but not everywhere differentiable Lyapunov function of a similar structure. The main theorem on sufficient conditions for system stabilizability with the help of piecewise affine control is stated and proved. An algorithm for constructing such a control and a Lyapunov function in a small neighborhood of the zero equilibrium is proposed. An example of numerical solution of the stabilization problem for a specific model system in three-dimensional space is considered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
The symbol “\(\preceq \)” corresponds to the componentwise inequality for vectors of the same length.
REFERENCES
Krasovskii, N.N., Problems of stabilization of controlled motions, in Teoriya ustoichivosti dvizheniya. Dopolnenie 4 (Theory of Motion Stability. Addendum 4), Malkin, I.G., Ed., Moscow, 1966, pp. 475–515.
Giesl, P. and Hafstein, S., Existence of piecewise linear Lyapunov functions in arbitrary dimensions, Discrete Contin. Dyn. Syst., 2012, vol. 32, no. 10, pp. 3539–3565.
Baier, R. and Hafstein, S., Numerical computation of control Lyapunov functions in the sense of generalized gradients, 21st Int. Symp. Math. Theory Networks Syst. (MTNS 2014) (Groningen, 2014), pp. 1173–1180.
Atanesyan, A.A. and Tochilin, P.A., Problem of stabilizing a switching system using a piecewise-linear control system, Moscow Univ. Comput. Math. Cybern., 2019, vol. 43, pp. 166–176.
Kurzhanskii, A.B. and Tochilin, P.A., Weakly invariant sets of hybrid systems, Differ. Equations, 2008, vol. 44, no. 11, pp. 1585–1594.
Tochilin, P.A., On constructing a piecewise affine value function in the optimal control problem on an infinite time horizon, Tr. Inst. Mat. Mekh. Ural. Otd. Ross. Akad. Nauk, 2020, vol. 26, no. 1, pp. 223–238.
Barbashin, E.A., Vvedenie v teoriyu ustoichivosti (Introduction to Stability Theory), Moscow: Nauka, 2014.
Krasovskii, N.N., Nekotorye zadachi teorii ustoichivosti dvizheniya (Some Problems of Motion Stability Theory), Moscow: Izd. Fiz.-Mat. Lit., 1959.
Schrijver, A., Theory of Linear and Integer Programming, Chichester–NY–Brisbane–Toronto–Singapore: Wiley-Interscience, 1986. Translated under the title: Teoriya lineinogo i tselochislennogo programmirovaniya, Moscow: Mir, 1991.
Kaplunova, E.P. and Tochilin, P.A., The problem of target control for a quadrotor when moving in a horizontal plane avoiding obstacles, Moscow Univ. Comput. Math. Cybern., 2021, vol. 45, pp. 152–167.
Funding
The results in Secs. 1–4 were obtained with the financial support of the Russian Science Foundation, project no. 22-11-00042. The results in Sec. 5 were obtained with the support of the Ministry of Science and Higher Education of the Russian Federation as part of the implementation of the program of the Moscow Center for Fundamental and Applied Mathematics under agreement no. 075-15-2022-284.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by V. Potapchouck
Rights and permissions
About this article
Cite this article
Tochilin, P.A. On Constructing a Piecewise Affine Stabilizer for a Nonlinear System. Diff Equat 58, 1538–1548 (2022). https://doi.org/10.1134/S0012266122011009X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0012266122011009X