On Instability in Systems with an Integral Invariant

Abstract

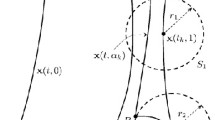
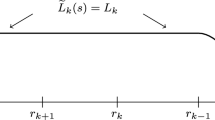
A theorem on the instability of an equilibrium in an autonomous system of differential equations with an integral invariant is proved: if in some neighborhood $B$ of the equilibrium there exists a function $V$ with nonnegative derivative $\dot {V}$ along the trajectories of the system and with $\dot {V}>0$ at some points of $B$ arbitrarily close to the equilibrium, then the equilibrium is unstable. In contrast to the classical Lyapunov–Chetaev–Krasovskii theorems, no restrictions are imposed on the properties of the function $V$ itself in the vicinity of the equilibrium.