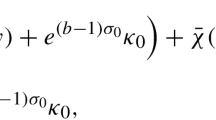Abstract
In the present paper, we give a new treatment of the mechanism of generation of chaotic dynamics in a perturbed conservative system in a neighborhood of the separatrix contour of a hyperbolic singular point of the unperturbed system. We theoretically prove and justify by three numerical examples of classical Hamiltonian systems with one and a half degrees of freedom and by an example of a simply conservative three-dimensional system that the complication of the dynamics in a conservative system as the perturbation increases is caused by a nonlocal effect of multiplication of hyperbolic and elliptic cycles (and the tori surrounding them), which has nothing in common with the mechanism of separatrix splitting in classical Hamiltonian mechanics.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Poincaré, H., Izbrannye trudy. T. 1. Novye metody nebesnoi mekhaniki (Selected Works in Three Volumes. Vol. 1. New Methods in Celestial Mechanics), Moscow: Nauka, 1971.
Arnol’d, V.I., Kozlov, V.V., and Neishtadt, A.I., Matematicheskie aspekty klassicheskoi i nebesnoi mekhaniki. Dinamicheskie sistemy 3 (Mathematical Aspects of Classical and Celestial Mechanics. Dynamical Systems 3), Moscow: Akad. Nauk SSSR, 1985.
Kozlov, V.V., Simmetrii, topologiya i rezonansy v gamil’tonovoi mekhanike (Symmetries, Topology and Resonances in Hamiltonian Mechanics), Izhevsk: Udmurt. Gos. Univ., 1995.
Treshchev, D.V., Gamil’tonova mekhanika (Hamiltonian Mechanics), Moscow, 2006.
Gel’freikh, V.G. and Lazutkin, V.F., Splitting of Separatrices: Perturbation Theory and Exponential Smallness, Uspekhi Mat. Nauk, 2001, vol. 56, no. 3 (339), pp. 79–142.
Loskutov, A.Yu., Dynamic Chaos. Systems of Classical Mechanics, Uspekhi Fiz. Nauk, 2007, vol. 177, no. 9, pp. 990–1015.
Likhterberg, A. and Liberman, M., Regulyarnaya i stokhasticheskaya dinamika (Regular and Stochastic Dynamics), Moscow, 2000.
Zaslavskii, G.M. and Sagdeev, R.Z., Vvedenie v nelineinuyu fiziku: Ot mayatnika do turbulentnosti i khaosa (Introduction to Nonlinear Physics: From Pendulum to Turbulency and Chaos), Moscow, 1988.
Magnitskii, N.A., Universal Theory of Dynamic and Space-Time Chaos in Complex Systems, Dinam. Slozhn. Sist., 2007, vol. 1, no. 1, pp. 18–39.
Magnitskii, N.A. and Sidorov, S.V., Application of the Feigenbaum-Sharkovskii-Magnitskii Theory to the Analysis of Hamiltonian Systems, Differ. Uravn., 2007, vol. 43, no. 11, pp. 1474–1479.
Magnitskii, N.A., A New Approach to the Analysis of Hamiltonian and Conservative Systems, Differ. Uravn., 2008, vol. 44, no. 12, pp. 1618–1627.
Author information
Authors and Affiliations
Additional information
Original Russian Text © N.A. Magnitskii, 2009, published in Differentsial’nye Uravneniya, 2009, Vol. 45, No. 5, pp. 647–654.
Rights and permissions
About this article
Cite this article
Magnitskii, N.A. On the nature of dynamic chaos in a neighborhood of a separatrix of a conservative system. Diff Equat 45, 662–669 (2009). https://doi.org/10.1134/S0012266109050048
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0012266109050048