Skip to main content
SpringerLink
Log in

On the Partial Stability in Probability of Nonlinear Stochastic Systems

  • Stochastic Systems
  • Published:
Automation and Remote Control Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

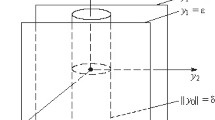
Abstract

A general class of the nonlinear time-varying systems of Itô stochastic differential equations is considered. Two problems on the partial stability in probability are studied as follows: 1) the stability with respect to a given part of the variables of the trivial equilibrium; 2) the stability with respect to a given part of the variables of the partial equilibrium. The stochastic Lyapunov functions-based conditions of the partial stability in probability are established. In addition to the main Lyapunov function, an auxiliary (generally speaking, vector-valued) function is introduced for correcting the domain in which the main Lyapunov function is constructed. A comparison with the well-known results on the partial stability of the systems of stochastic differential equations is given. An example that well illustrates the peculiarities of the suggested approach is described. Also a possible unified approach to analyze the partial stability of the time-invariant and time-varying systems of stochastic differential equations is discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Khas’minskii, R.Z., Ustoichivost’ sistem differentsial’nykh uravnenii pri sluchainykh vozmushcheniyakh ikh parametrov, Moscow: Nauka, 1969. Translated under the title Stochastic Stability of Differential Equations, Alphen aan den Rijn: Sijthoff & Noordhoff, 1980.

    Google Scholar 

  2. Kushner, H.J., Stochastic Stability and Control, New York: Academic, 1967. Translated under the title Stokhasticheskaya ustoichivost’ i upravlenie, Moscow: Mir, 1969.

    MATH  Google Scholar 

  3. Mao, X.R., Stochastic Differential Equations and Applications, Oxford: Woodhead, 2008, 2nd ed.

    Book  Google Scholar 

  4. Kats, I.Ya. and Krasovskii, N.N., On the Stability of Systems with Random Parameters, J. Appl. Math. Mech., 1960, vol. 24, no. 5, pp. 809–823.

    Article  Google Scholar 

  5. Kats, I.Ya. and Martynyuk, A.A., Stability and Stabilization of Nonlinear Systems with Random Structure, London: Taylor & Francis, 2002.

    Book  MATH  Google Scholar 

  6. Mao, X.R. and Yuan, C.G., Stochastic Differential Equations with Markovian Switching, London: Imperial College Press, 2006.

    Book  MATH  Google Scholar 

  7. Vorotnikov, V.I., Two Classes of Partial Stability Problems: Unification of the Notions and Common Conditions of Solvability, Dokl. Physics, 2002, vol. 47, no. 5, pp. 377–381.

    Article  Google Scholar 

  8. Vorotnikov, V.I. and Martyshenko, Yu.G., On Partial Detectability of the Nonlinear Dynamic Systems, Autom. Remote Control, 2009, vol. 70, no. 1, pp. 20–32.

    Article  MathSciNet  MATH  Google Scholar 

  9. Vorotnikov, V.I. and Martyshenko, Yu.G., On the Partial Stability of Nonlinear Dynamical Systems, J. Comp. Syst. Sci. Int., 2010, vol. 49, no. 5, pp. 702–709.

    Article  MathSciNet  MATH  Google Scholar 

  10. Vorotnikov, V.I., Partial Stability and Control: The State of the Art and Developing Prospects, Autom. Remote Control, 2005, vol. 66, no. 4, pp. 511–561.

    Article  MathSciNet  MATH  Google Scholar 

  11. Vorotnikov, V.I. and Martyshenko, Yu.G., Stability in a Part of Variables of “Partial” Equilibria of Systems with Aftereffect, Math. Notes, 2014, vol. 96, no. 4, pp. 477–483.

    Article  MathSciNet  MATH  Google Scholar 

  12. Vorotnikov, V.I. and Martyshenko, Yu.G., On the Partial Stability of Nonlinear Discrete Systems, Mekhatr. Avtomatiz. Upravlen., 2017, vol. 18, no. 6, pp. 371–375.

    Article  Google Scholar 

  13. Ramirez-Llanos, E. and Martinez, S., Distributed and Robust Fair Optimization Applied to Virus Diffusion Control, IEEE Trans. Network Sci. Eng., 2017, vol. 4, no. 1, pp. 41–54.

    Article  MathSciNet  MATH  Google Scholar 

  14. Sharov, V.F., Stability and Stabilization of Stochastic Systems with Respect to Part of the Variables, Autom. Remote Control, 1978, vol. 39, no. 11, pp. 1629–1636.

    MATH  Google Scholar 

  15. Vorotnikov, V.I., Partial Stability and Control, Boston: Birkhauser, 1998.

    MATH  Google Scholar 

  16. Potcovaru, G., On the Partial Stability of a Dynamical Systems with Random Parameters, An. Univ. Bucur. Mat., 1999, vol. 48, no. 2, pp. 163–168.

    MathSciNet  MATH  Google Scholar 

  17. Ignatyev, O., Partial Asymptotic Stability in Probability of Stochastic Differential Equations, Statist. Probab. Lett., 2009, vol. 79, no. 5, pp. 597–601.

    Article  MathSciNet  MATH  Google Scholar 

  18. Ignatyev, O., New Criterion of Partial Asymptotic Stability in Probability of Stochastic Differential Equations, Appl. Math. Comp., 2013, vol. 219, no. 23, pp. 10961–10966.

    Article  MathSciNet  MATH  Google Scholar 

  19. Zuev, A.L., Ignatyev, A.O., and Kovalev, A.M., Ustoichivost’ i stabilizatsiya nelineinykh sistem (Stability and Stabilization of Nonlinear Systems), Kiev: Naukova Dumka, 2013.

    Google Scholar 

  20. Rajpurohit, T. and Haddad, W.M., Stochastic Finite-Time Partial Stability, Partial-State Stabilization, and Finite-Time Optimal Feedback Control, Math. Control, Signals, Syst., 2017, vol. 29, no. 2, art. 10.

    Google Scholar 

  21. Rajpurohit, T. and Haddad, W.M., Partial-State Stabilization and Optimal Feedback Control for Stochastic Dynamical Systems, J. Dynam. Syst., Measurement, Control, 2017, vol. 139, no. 9, p. DS–15–1602.

    Article  Google Scholar 

  22. Rumyantsev, V.V. and Oziraner, A.S., Ustoichivost’ i stabilizatsiya dvizheniya po otnosheniyu k chasti peremennykh (Stability and Stabilization of Motion with Respect to Part of the Variables), Moscow: Nauka, 1987.

    MATH  Google Scholar 

  23. Miroshnik, I.V., Nikiforov, V.O., and Fradkov, A.L., Nelineinoe i adaptivnoe upravlenie slozhnymi dinamicheskimi sistemami (Nonlinear and Adaptive Control of Complex Dynamic Systems), St. Petersburg: Nauka, 2000.

    MATH  Google Scholar 

  24. Rumyantsev, V.V., On Motion Stability with Respect to Part of the Variables, Vestn. Mosk. Gos. Univ., Ser. Mat. Mekh. Fiz. Astronom. Khim., 1957, no. 4, pp. 9–16.

  25. Vorotnikov, V.I., On the Theory of Partial Stability, J. Appl. Math. Mech., 1995, vol. 59, no. 4, pp. 525–531.

    Article  MathSciNet  MATH  Google Scholar 

  26. Kao, Y., Wang, C., Zha, F., and Cao, H., Stability in Mean of Partial Variables for Stochastic Reaction-Diffusion Systems with Markovian Switching, J. Franklin Inst., 2014, vol. 351, no. 1, pp. 500–512.

    Article  MathSciNet  MATH  Google Scholar 

  27. Socha, L. and Zhu, Q.X., Exponential Stability with Respect to Part of the Variables for a Class of Nonlinear Stochastic Systems with Markovian Switching, Math. Comp. Simul., 2019, vol. 155, pp. 2–14.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ural Federal University, Yekaterinburg, Russia

    V. I. Vorotnikov

  2. Gubkin Russian State University of Oil and Gas (National Research University), Moscow, Russia

    Yu. G. Martyshenko

Authors
  1. V. I. Vorotnikov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu. G. Martyshenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. I. Vorotnikov or Yu. G. Martyshenko.

Additional information

Russian Text © The Author(s), 2019, published in Avtomatika i Telemekhanika, 2019, No. 5, pp. 86–98.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vorotnikov, V.I., Martyshenko, Y.G. On the Partial Stability in Probability of Nonlinear Stochastic Systems. Autom Remote Control 80, 856–866 (2019). https://doi.org/10.1134/S0005117919050059

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0005117919050059

Keywords

Search

Navigation