Abstract
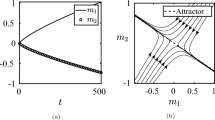
We study stabilization processes in resource networks with arbitrary topology for large values of the resource, when certain vertices accumulate the resource, and resource in these vertices exceeds output bandwidth. We introduce the notion of flow in a network and study monotone and nonmonotone flows. We prove existence and uniqueness for the limit flow and, as a corollary, of the limit state. We introduce the notion of a potential attractor and study networks with one and several attractors. We show that in networks with several potential attractors, in case of large resources the limit state depends on the initial state.
Similar content being viewed by others
References
Kuznetsov, O.P., Uniform Resource Networks. I. Complete Graphs, Autom. Remote Control, 2009, vol. 70, no. 11, pp. 1889–1900.
Zhilyakova, L.Yu., Asymmetrical Resource Networks. I. Stabilization Processes for Low Resources, Autom. Remote Control, 2011, vol. 72, no. 4, pp. 798–807.
Kuznetsov, O.P. and Zhilyakova, L.Yu., Complete Two-Sided Resource Networks with Arbitrary Bandwidths, Upravlen. Bol’shimi Sist., 2010, no. 30.1, pp. 640–664.
Erzin, A.I. and Takhonov, I.I., The Balanced Flow Problem, Sib. Zh. Ind. Mat., 2006, vol. 9, no. 4(28), pp. 50–63.
Gantmakher, F.R., Teoriya matrits (Theory of Matrices), Moscow: Fizmatlit, 2004. Translated under the title The Theory of Matrices, New York: Chelsea, 1959.
Kemeny, J. and Snell, J., Finite Markov Chains, Princeton: Van Nostrand, 1960. Translated under the title Konechnye tsepi Markova, Moscow: Nauka, 1970.
Author information
Authors and Affiliations
Additional information
Original Russian Text © L.Yu. Zhilyakova, 2012, published in Avtomatika i Telemekhanika, 2012, No. 6, pp. 103–118.
Rights and permissions
About this article
Cite this article
Zhilyakova, L.Y. Asymmetric resource networks. II. Flows for large resources and their stabilization. Autom Remote Control 73, 1016–1028 (2012). https://doi.org/10.1134/S0005117912060070
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0005117912060070