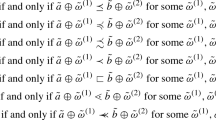Skip to main content
SpringerLink
Log in

Existence of Bargaining Sets for Cooperative Games with Fuzzy Payoffs

  • Research Articles
  • Published:
Mathematical Notes Aims and scope Submit manuscript

Abstract

It is proved that the bargaining set for a cooperative game with trapezoidal fuzzy payoffs is nonempty.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. J. Aumann and M. Maschler, “The bargaining set for bargaining games,” in Advances in Game Theory, Ed. by M. Dresher, L. S. Shapley and A. W. Tucker (Princeton Univ. Press, Princeton, 1964), pp. 443–476.

    Google Scholar 

  2. M. Davis and M. Maschler, “Existence of stable payoff configurations for bargaining games,” Bull. Amer. Math. Soc. 69, 106–108 (1963).

    Article  MathSciNet  MATH  Google Scholar 

  3. B. Peleg, “Existence theorem for the bargaining set \(\mathscr M_1^{(i)}\),” Bull. Amer. Math. Soc. 69, 109–110 (1963).

    Article  MathSciNet  MATH  Google Scholar 

  4. B. Peleg, “Existence theorem for the bargaining set \(\mathscr M_1^{(i)}\),” in Essays in Mathematical Economics (In Honor of Oskar Morgenstern), Ed. by M. Shubik (Princeton Univ. Press, Princeton, 1967), pp. 53–56.

    Chapter  Google Scholar 

  5. M. J. Osborne and A. Rubinstein, A Course in Game Theory (MIT Press, Cambridge, MA, 1994).

    MATH  Google Scholar 

  6. B. Peleg and P. Sudhölter, Introduction to the Theory of Cooperative Games (Springer- Verlag, Heidelberg, 2007).

    MATH  Google Scholar 

  7. K.-I. Shimomura, “The bargaining set and coalition formation,” Int. J. Econ. Theory 18 (1), 16–37 (2022).

    Article  MathSciNet  MATH  Google Scholar 

  8. J. Liu, X. Liu, Y. Huang, and W. Yang, “Existence of an Aumann–Maschler fuzzy bargaining set and fuzzy kernels in TU fuzzy games,” Fuzzy Sets and Systems 349, 53–63 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  9. Y. Huang, D. Bi, J. Liu, X. Liu, and M. Wang, “Existence of fuzzy prekernels and Mas-Colell bargaining sets in TU games,” Fuzzy Sets and Systems 362, 71–84 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  10. X. Yu, H. Zhou, X. Zhang, Q. Zhang, Y. Liu, and J. Pang, “The fuzzy bargaining set of a bargaining game with fuzzy coalition,” J. Intelligent and Fuzzy Systems 33, 1757–1765 (2017).

    Article  MATH  Google Scholar 

  11. X. Zhang, H. Sun, G. Xu, and D. Hou, “On the core, nucleolus and bargaining sets of bargaining games with fuzzy payoffs,” J. Intelligent and Fuzzy Systems 36, 6129–6142 (2019).

    Article  Google Scholar 

  12. G. Bortolan and R. Degani, “A review of some methods for ranking fuzzy subsets,” Fuzzy Sets and Systems 15 (1), 1–19 (1985).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National Research University Higher School of Economics, Moscow, 101000, Russia

    A. S. Shvedov

Authors
  1. A. S. Shvedov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. S. Shvedov.

Additional information

Translated from Matematicheskie Zametki, 2023, Vol. 114, pp. 615–622 https://doi.org/10.4213/mzm13629.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shvedov, A.S. Existence of Bargaining Sets for Cooperative Games with Fuzzy Payoffs. Math Notes 114, 619–624 (2023). https://doi.org/10.1134/S0001434623090298

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0001434623090298

Keywords

Search

Navigation